线段图在解形如ax±x=b 方程中的妙用

楼香君

[摘 要]解决数学题时，作图是常用的利器，如集合图、线段图、象形图等。学会画图，是形成解题谋略的基础，尤其是线段图，在解形如ax±x=b的方程中发挥着巨大的作用。

[关键词]作图法;作图能力;低年级

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）05-0063-03

线段图，就是通过线段长短来反映数量大小，通过多条线段长短比例和拼接关系来反映数量关系，具有直观、简洁、实用的特点，它在解决和差、和倍、分数（百分数）问题，以及路程问题等题型时优势明显。学生在解题时，先通过仔细审题，过滤掉其中的非数学因素，分析出各个数量结构和分解组合变化情况后，再画出线段图，然后根据线段图直观地概括出数量关系，便可列式解决问题。但在教学实践中，部分教师，特别是中低年级的教师认为，面对简单问题时画线段图纯属多此一举，这造成学生的作图解题能力长期得不到应有的锻炼;到了高年级，问题变得繁复而不得不使用线段图时，才临时抱佛脚，却为时已晚。学生常常因为画的图驴唇不对马嘴，直接影响解题技能的发挥。

学会画图，是学生形成解题谋略的基础，因此作图能力的训练培养应从低年级抓起。下面笔者以北师大版教材四年级下册“解形如ax±x=b的方程”一课为例，分享作图法教学的一些经验。

一、课前思考

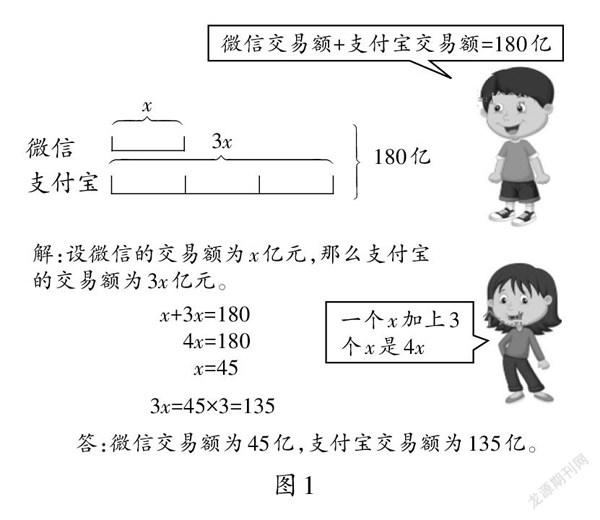
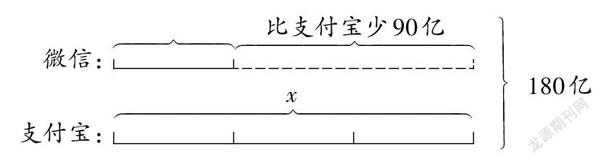
【例】“双十一”时，支付宝交易额是微信交易额的3倍，全网线上购物成交额为180亿。支付宝的交易额比微信的交易额多出90亿。国内两大电商巨头的交易额各是多少？

<D：＼数据＼小学教学参考（数学）202202＼2s23.tif>[ ][ ][微信交易额+支付宝交易额=180亿

][微信

支付宝][解：设微信的交易额为x亿元，那么支付宝的交易额为3x亿元。][答：微信交易额为45亿，支付宝交易额为135亿。][一个x加上3个x是4x][180亿][x+3x=180

4x=180

x=45][3x=45×3=135] [x][3x]

上题是继“认识方程”“等式性质”后安排在解方程中的例题。毋庸赘言，题中所给条件非常充足，编者意图以丰富的条件誘导学生灵活自由地运用各种数量关系列方程，从多角度解答形如ax±x=b的方程。教材在题后呈现了线段图，直观揭示了数量关系“支付宝交易额+微信交易额=180亿”。对于教材如此设计，笔者满腹狐疑：新教材并未单设章节教学线段图，线段图先前只在四年级上册的“行程问题”中惊鸿一瞥，马上销声匿迹;之后在五年级上册的“相遇问题”、五年级下册的“分数混合运算”中也是“犹抱琵琶半遮面”。笔者查阅其他版本的教材也有类似现象，只有苏教版教材在四年级下册安排了“画图策略”的专题讲解。这种躲躲藏藏的做法，不但破坏了教材的完整性，而且把解决问题和分析线段图并在一起授课，势必会加大任务量，造成课程超载。因为目前学生尚无能力根据题意绘制线段图，而无法正确熟练地绘制线段图，建立在图解之上提取数量关系列方程就会成为空中楼阁。教学中，如何才能做到解题和作图两全其美、统筹兼顾呢？如何“榨干”线段图这根“拐杖”的价值呢？为此，笔者对教材稍加改进。

线段图作为一种直观的教学手段，在小学数学教学中一直都有着举足轻重的地位。这种教学法与学生平时所见所用的示意图存在很大差异，它是经过几何抽象化处理的示意图，不但具有会意的作用，还有展示数量关系的功能。学生由一般的象形图进入线段图的世界，一下子很难适应。学生习惯用“和差倍分”来分析数量关系，对这种用线段长度表示数量多少与比例的表征还未能建立对应的思维接口。之前学生解决的一般都是代数问题，而线段图其实就是相当于将代数问题几何化，但又不是传统意义上的数形结合。传统意义上的数形结合中，数据属性与几何形态存在很大的相似性和可比性。例如行程问题中的路程本身就是直线路线，所以用线段表示路程再贴切不过了;如果是数量比较问题，就用几何符号代替不同的事物。而线段图则是抽象化后的数量，完全脱离实物形象，因此，学生需要一个循序渐进的“爬坡”过程。

二、教学过程

（一）呈现线段图

1.直接出示

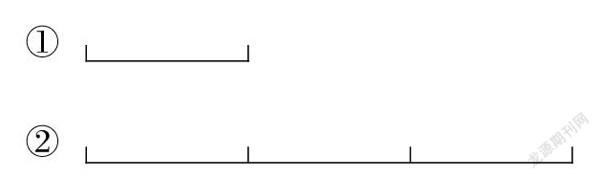
出示：

师：观察上面2条线段，有什么发现？

（线段②长度有3份，相当于3条线段①的长度;线段②的长度比线段①的长度多出2份）

2.完善关系

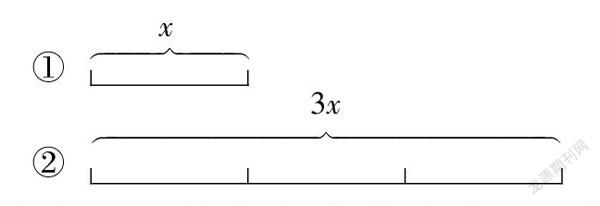
师：如果用含有未知数的代数式来表示线段长度，你觉得应如何表示？（用x表示1个单位长度，线段②的长度可用3x表示）

板书：

师：如果已知两条线段的总长是180，你能计算出单位长度x的具体值吗？

（学生独立思考）

3.初步解决

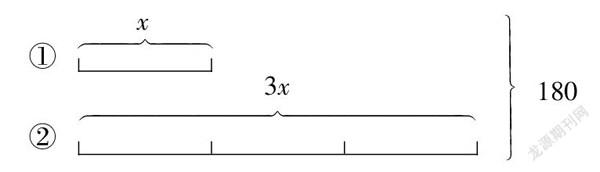
板书：x+3x=180 ⇒ 4x=180 ⇒ x=45

师：请谈谈你的思路。（数量关系：1个x+3个x=180）

此处，将线段图表示数量关系与列方程有机结合起来：列方程解决问题的第一步是设未知数，然后分析题中的数量关系，再列出方程。而为列方程提供的数量关系需要先将未知数作为数量关系的一部分，再分析出包含未知量的数量关系，这与画线段图分析数量关系有着微妙的联系：线段图里不同线段之间有着包含与被包含的关系，可以根据需要设定其中任意一条线段为未知数，或者设定其中特定的一条线段为未知数，而且几条线段之间的长度关系刚好就是等量关系，这为列方程做好了准备。

线段图是从情境中抽离数量关系后的简图，具有一定的几何直观性，但是线段图中不同的数量是用不同的线段表示的。因此，各个数量之间到底存在什么样的纵向关系，仅仅从线段上是看不出来的，这就需要进行勾连。方程无疑是最好的连接链条，因为列方程需要等量关系，这个等量关系就是各条线段之间的纵向关系;而各线段之间的横向倍比关系就是为了统一计量标准，也就是为了用含有同一个未知数的代数式表示各条线段的数量大小。这样线段图的横向关系和纵向关系就被方程完美地联结到一起，这比单纯根据原题列方程容易得多。

（二）自主建构

1.情境对接

师：根据线段图展开联想，你觉得可以赋予它们哪些现实情境？

（学生众说纷纭，有的说两个施工队的施工问题，有的说两个商店某天的营业额问题，也有的说支付宝和微信某个季度的交易额问题。）

师：我们就用支付宝和微信交易额问题继续研究。

学生对线段图的模式掌握到一定程度后，教师就可以抽离具体情境，让学生自己根据线段图中蕴含的数量关系来赋予问题情境，编写题目，这样教学可以进一步深化学生对线段图的理解。再加上直接在线段上写未知数等于是跳脱了问题情境而列出方程的雏形，这对学生透过情境表象提取数量关系列方程大有裨益。

这一环节的设计可谓独具匠心，为了让学生接受线段图的抽象性，先出示一幅线段图，标识出各个数据及其纵向关系，然后让学生根据这种带有半方程半线段图性质的“数形图”来编写情境。学生可以发挥自己的想象力，凭借自己的经验，根据纵向和横向的数量关系来合理编写恰当的故事情节，只要合情合理，数量关系与“数字图”吻合即可。学生通过不同情境的编排和设计，进一步发现线段图的抽象性和简练性，不仅对线段图的特性有进一步的认识，而且在以后分析题意时，即使没有线段图，也能一眼洞穿数量关系这个“要害”，自动忽略次要因素。

2.深入研究

师：刚才列的方程“x+3x=180”在移动支付的情境中凭借的等量关系是什么？（支付宝交易额+微信交易额=180亿）除了这个等量关系，还有没有其他的？请绘出线段图，然后根据线段图来列方程。

（学生独立操作，教师巡视）

3.展示分享

师（指名汇报）：说说你的构图方略，并展示所列方程。

学生展示：

解法一：设微信交易额x亿，支付宝交易额x+90亿。

x+（x+90）=180⇒2x+90=180?2x=90⇒x=45⇒x+90=45+90=135。

解法二：设微信交易额x亿，支付宝交易额3x亿。

3x-x=90⇒2x=90⇒x=45⇒3x=45×3=135。

解法三：设支付宝交易额x亿。

x+（x-90）=180⇒2x-90=180⇒2x=270⇒x=135⇒x-90=135-90=45。

4.对比反思

师：上述4种方法，你更钟爱哪一种？你觉得线段图在此处扮演着什么角色？今天所列方程与之前所列方程有何不同？（含有2个未知数）

原题为了训练学生多维度分析线段图的能力，给出了两个表示纵向关系的条件，一个是“全网线上购物成交额为180亿”，另一个是“支付宝的交易额比微信的交易额多90亿”。有了这两个重复的纵向条件，学生就可以基于不同的等量关系列出不同的方程。无论是哪种方程，都只是各线段的纵向关系发生调整，横向的倍比关系并未发生改变。这种训练不但拓宽了学生分析线段图的视野，而且增强了学生分析线段图的灵活性。

三、课后反思

如果把数量关系比作“根”，那么情境就是“枝叶”。

1.先扎根后披绿。为了体现线段图的功用，可一改教材的通行做法，将情境之“枝叶”后置，直接出示线段图，如此数量关系昭然若揭，方程也呼之欲出。直观的线段图一开始就刻印在学生的脑海中，再去思考“这个线段图可以赋以何种情境”，前面深深“扎根”，后面自然会“枝繁叶茂”，各种合理有趣的情境如雨后春笋般冒出。教学实践表明：学习解决形如ax±x=b的方程，提取等量关系是关口，难点是两边的数量里都含有未知数;而这个数量关系通过线段图展示可一览无遗，条分缕析，“扎根”成功了，再想象情境就如同开枝散叶。至此，学生对线段图的作用和画法也就略有所知了。

2.平稳过渡。在学生首次经历从“线段图”中提取数量关系后，笔者让学生进一步尝试“画线段图”，只需谈画法和感想，避免因难度陡增而吓退学生。学生的思维方式不同，所作线段图和所列方程自然不同，学生给出了三种方案，但是无一例外都是运用已有的数量关系。汇报交流的过程中，学生相互启迪智慧，交换意见，对线段图的画法有了统一、成熟的认识，表述趋向规范，其体验也愈加深刻。从“初识线段图—绘制线段图—解说线段图”到最终“反思线段图有什么作用”这层层递进的活动，不但有效地培养了学生的画图能力，而且增强了学生的运用意识，成效斐然。

3.优势尽显。事实表明，从中低年级就开始引导学生画线段图是明智之举。线段图作为一种直观手段，是帮学生从形象思维向抽象思维转型的利器，它是数形结合思想的雏形，有助于培养学生数学核心素养。教师应不遗余力地帮助学生识图、读图、作图、释图，强化他们的图形意识，提升他们的作图能力，使他们可以在图文间穿梭自如。更重要的是，教师应在长期的训练中让学生充分运用作图优势，让作图习惯深深植根于学生的潜意识里。唯有如此，学生到了高年级时才不会遭遇“巧妇难为无米之炊”的窘境。

综上可知，切不可在中低年级教学时敷衍了事，跳过作图教学，直接从文字层面分析数量关系。这样做虽苟安一时，但后患无穷。

（责编 罗 艳）