从两个视角探究圆锥曲线中的定值问题

⦿甘肃省天水市第一中学 方春丽

1 引言

在圆锥曲线问题中，常常出现定点定值问题.求解的思路主要有两个：一是利用代数的解法求解，即先选择恰当的基本量，表示出所有的信息，利用代数运算求得结论，再对计算结果进行几何化的解释；二是直接利用圆锥曲线的几何性质进行求解.两种方法并不独立，有时也需要配合使用进行证明.在2022届汕头市的质量检测中，考查了一道以椭圆为背景的定值问题，笔者分别从代数与几何的视角进行了证明，并将该结论推广至双曲线与抛物线.现将探究过程展示如下，以飨读者.

2 题目及分析

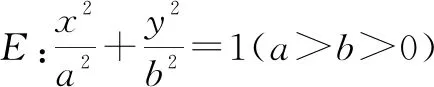
(1)求椭圆E的方程；

(2)若动直线l与椭圆E有且只有一个公共点，过点M(1,0)作直线l的垂线，垂足为Q，试探究：|OQ|是否为定值，如果是，则求出该值；如果不是，则说明理由.

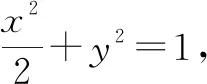
3 解法呈现

解法1：基本量法.

设直线l的方程为x=my+t，与椭圆E联立，可得(m2+2)y2+2mty+t2-2=0.因为直线l与椭圆E有且只有一个公共点，所以上式的判别式等于零.

化简可得：t2=m2+2.

①

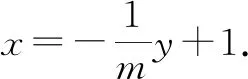
②

将式②代入直线l的方程，可得

③

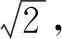
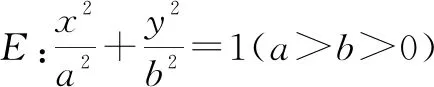
将上述解法一般化即可证明上述结论成立.接下来，笔者将通过几何的视角来证明.

解法2：利用极点极线，应用几何法求解.

在证明结论之前，先介绍以下两个引理.

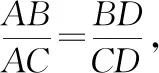
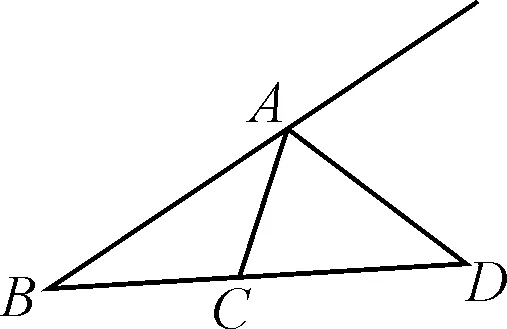
图1

证明:如图2,不妨设AB>AC(若AB=AC，则对应的点D不存在),在线段AB上找一点E，使得AE=AC，则∠3=∠4.

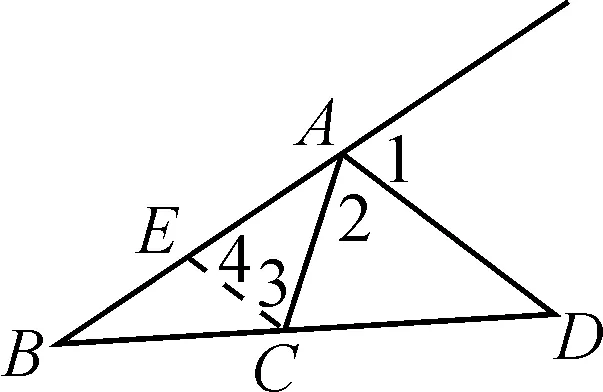
图2

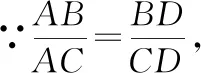
又∠B=∠B，

∴△BCE∽△BDA.

∴CE∥AD，

∴∠3=∠2，∠4=∠1.

因此∠1=∠2，即AD为△ABC对应的外角平分线.

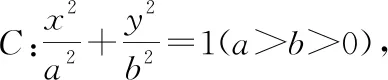
该引理即是椭圆的光学性质：若从椭圆的一个焦点发射出一束光线，经过椭圆反射后会经过椭圆的另一个焦点.

证明：如图3，设点P的坐标为(x0,y0).根据极点极线[2]的定义可得，过点P的切线l方程为

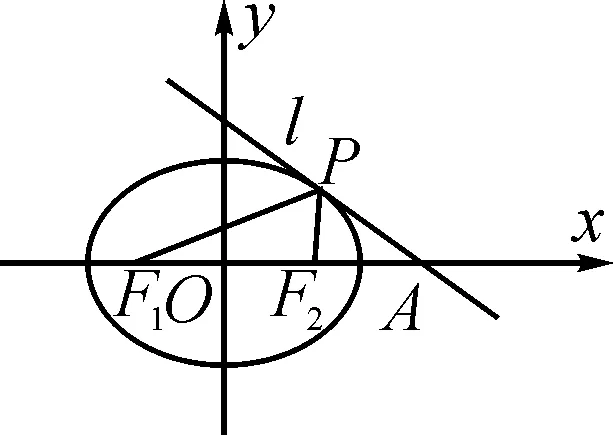
图3

当直线l与x轴无交点时，结论显然成立.

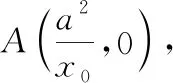
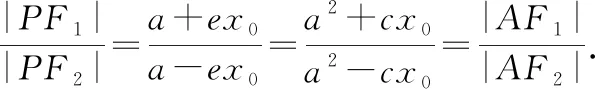
根据外角平分线定理，则可得椭圆过点P的切线为∠F1PF2的外角平分线.

现根据引理证明上述一般性结论.

证明：如图4，设切线l对应的切点为点A，椭圆E的左焦点为F1，连接MA.过M作切线l的垂线，垂足为Q.延长MQ并与F1A的延长线交于点M′.根据引理2可知，切线l是∠MAM′的角平分线.

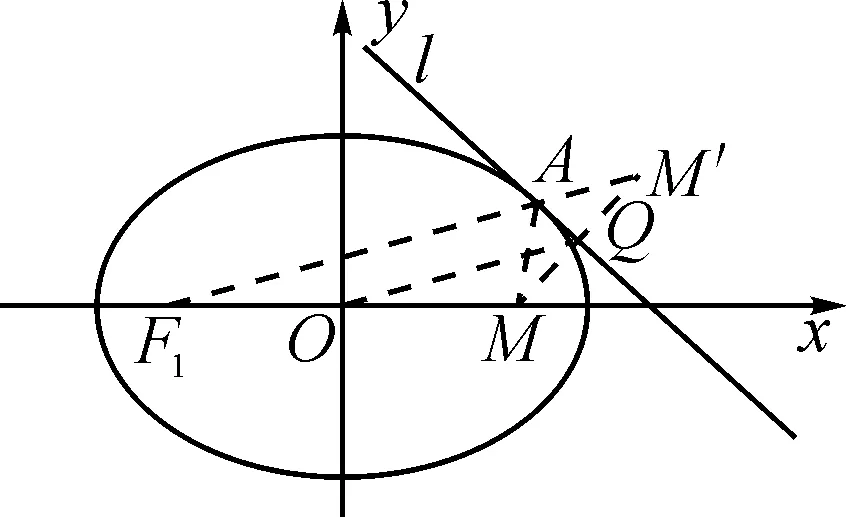
图4

考虑△MAM′，结合MM′⊥l可得△MAM′为等腰三角形，从而可得AM=AM′，且点Q为MM′的中点.

结合椭圆的定义可得|F1M′|=|F1A|+|AM′|=|F1A|+|MA|=2a.

在△F1MM′中，点O为F1M的中点，根据中位线的性质可得|OQ|=a成立.

根据引理2，切线l为∠MAM′的角平分线，且MM′⊥l，从而可得△MAM′为等腰三角形，且点Q为MM′的中点.

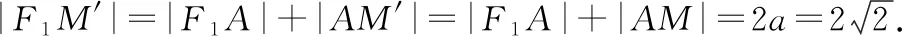
4 命题的拓展与练习

该问题的背景是椭圆，若将椭圆换成抛物线或双曲线，也有类似结论成立.

定理1：已知抛物线E:y2=2px(p>0)的焦点为M，若动直线l是抛物线E的切线，过点M作直线l的垂线，垂足为Q，则点Q的轨迹为y轴.

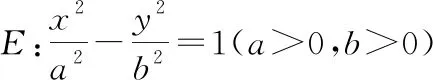
在椭圆以及双曲线中，所得的点Q的轨迹均为一个圆，所以所求的|OQ|的值为定值.在抛物线中，点Q的轨迹为直线，也可理解为半径无限大的圆.从这个意义来讲，三个圆锥曲线的意义相同.上述两个定理的证明过程可模仿椭圆中的证明方法即可，但需要了解双曲线与抛物线的光学性质.现简介如下：

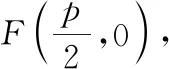
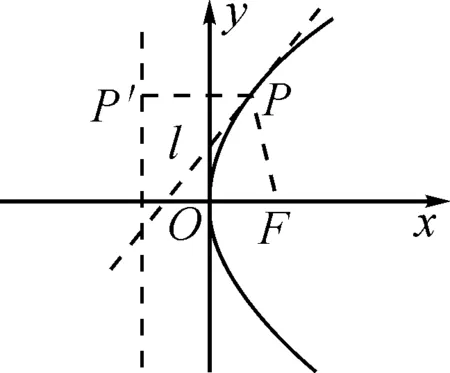
图5

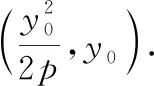
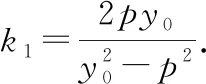
因此α=β.可知抛物线过点P的切线为∠FPP′的角平分线.

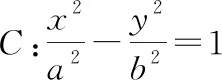
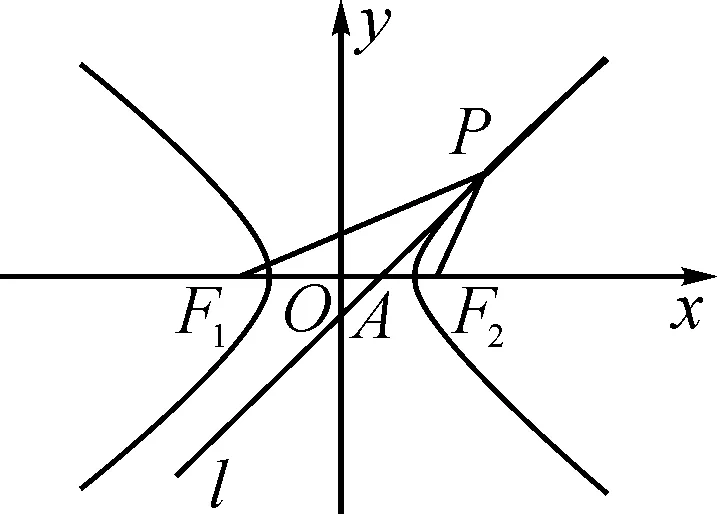
图6

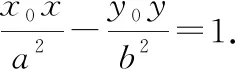
根据焦半径公式|PF1|=a+ex0，|PF2|=ex0-a，则有

根据角平分线定理，双曲线过点P的切线为∠F1PF2的角平分线.

根据上述定理，可命制出如下变式供大家练习.

例1已知抛物线E:y2=4x的焦点为M，若动直线l是抛物线E的切线，过点M作直线l的垂线，垂足为Q，求点Q的轨迹.

答案：直线x=0.

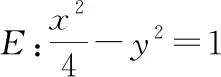
答案：|OQ|为定值，且|OQ|=2.

两个例题的证明过程相似，现简证例2如下：

如图7，设直线为l为双曲线E右支的一条切线，切点为点A，延长MQ与AF1交于点M′，根据引理4，切线l为∠F1AM的角平分线，且MM′⊥l，可得△MAM′为等腰三角形，并且点Q为MM′的中点.

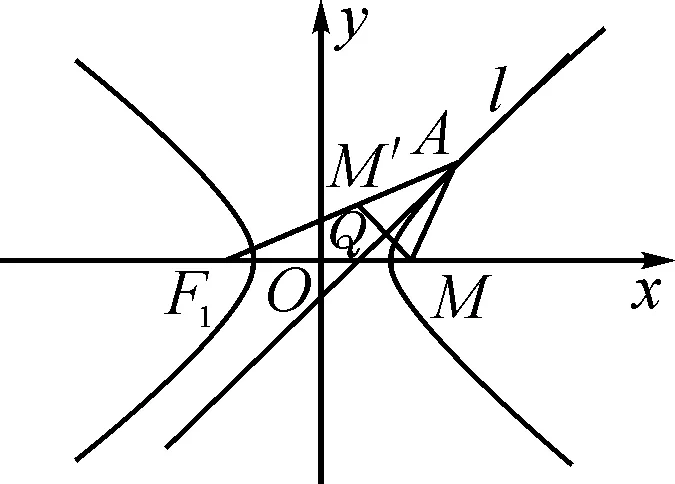
图7

当切线l为双曲线左支的切线时，证明方法与该证法相似，不再赘述.