一阶逻辑中几类特殊公式的真度计算方法

马 硕，惠小静，郝 娇

（延安大学数学与计算机科学学院，陕西延安 716000）

以王国俊为首的学者提出了计量逻辑学理论［1］，并建立了经典逻辑和模糊逻辑中公式真度理论［2-3］。这些理论很快引起了学术界的广泛关注，以此为基础大量学者针对不同的命题逻辑系统提出了公式真度的概念和基于真度的程度化推理方法［4-10］。不难发现以上成果都是在各种命题逻辑系统中基于语义方法建立的，由于一阶逻辑的语义理论远远较命题逻辑复杂，要在谓词逻辑中从语义途径建立真度理论并不容易，仅有少数学者做出一些尝试性的研究成果［11-13］。

本文的出发点是以全体不含函数符号的一阶闭逻辑公式之集Ф中公式的真度定义和真度映射τ具有的MP规则和真度运算性质［14］，以及谓词逻辑系统£∀的公理［15］为铺垫，对BL∀的重要扩张Łukasiewicz谓词逻辑系统Ł∀中的特殊公式展开公理化真度研究。其中£是基本命题逻辑BL的模式扩张，谓词逻辑系统£∀公理包含：ⅰ）£中的公理，其中A，B，C为谓词公式；ⅱ）带有量词的公理。从而为之后开展相关研究奠定基础。

1 预备知识

下面首先对Ф中公式真度的定义和真度映射τ具有的性质进行说明，设Ф表示全体不含函数符号的一阶闭逻辑公式之集，其中A，B，C等表示Ф中的一阶逻辑公式。

定义1.1［14］称映射τ：Ф→[0，1]为公理化真度映射，若以下条件成立：

（K1）不出现相同谓词符号的N个文字的完全闭包的合取的真度等于

（K2）若A是Ф中的定理，则τ(A)=1；

（K3）τ(¬A)=1-τ(A)，A∈Ф；

（K4）τ（A→B）+τ（A）=τ（B→A）+τ（B），A，B∈Ф；

（K5）τ(cl(¬Q))=1-τ(cl Q)；

（K6）在计算公式的真度时，其中原子公式中的变元可以相互替换。

当A∈Ф时，称τ(A)为A的公理化真度，简称为A的τ-真度或真度。

命题1.1［14］真度映射τ具有以下性质：

ⅰ）若A是矛盾式，则τ(A)=0；

ⅱ）若A与B逻辑等价，则τ(A)=τ(B)；

ⅲ）若τ(A→B)=1，则τ(A)≤τ(B)；

ⅳ）若τ(A)≥a，τ(A→B)≥b，则τ(B)≥a+b-1；

ⅴ）若τ(A→B)≥a，τ(B→C)≥b，则τ(A→C)≥a+b-1；

ⅵ）τ(A→C)≥τ(A→B)+τ(B→C)-1；

ⅶ）τ(A∨B)+τ(A∧B)=τ(A)+τ(B)。

由于Łukasiewicz谓词逻辑是BL谓词逻辑的扩张，因此下面对谓词逻辑的模式扩张做一简单介绍。

定义1.2［15］设£是基本命题逻辑BL的模式扩张。谓词逻辑系统£∀的公理包含以下两类：

ⅰ）£中的公理，其中A，B，C为谓词公式：

（BL1）(A→B)→((B→C)→(A→C))；

（BL2）A&B→A；

（BL3）A&B→B&A；

（BL4）A&(A→B)→B&(B→A)；

（BL5a）(A→(B→C))→(A&B→C)；

（BL5b）(A&B→C)→(A→(B→C))；

（BL6）((A→B)→C)→(((B→A)→C)→C)；

ⅱ）带有量词的公理：

（∀1）(∀x)A(x)→A(t)（在A(x)中 可 用t替代x）；

（∃1）A(t)→(∃x)A(x)（在A(x)中 可 用t替代x）；

（∀2）(∀x)(B→A)→(B→(∀x)A)（x在B中不自由）；

（∃2）(∀x)(A→B)→((∃x)A→B)（x在B中不自由）；

（∀3）(∀x)(A∨B)→((∀x)A∨B)（x在B中不自由）。

系统£∀的推理规则有以下两条：

MP规则：由A，A→B推出B；

推广规则：由A推出(∀x)A。

下面是对Łukasiewicz谓词演算系统中的公理和定理的说明。

为了将Łukasiewicz逻辑公理化，只需对BL的公理增加一个双重否定公理：

称BL+(¬¬)为命题演算系统，简称为Ł。

定义1.3［15］以下公式为Łukasiewicz公理：

命题1.2［15］ⅰ）Ł├¬¬A↔A；

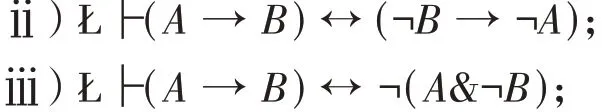
ⅳ）Ł├((A→B)→B)→((B→A)→A)。

命题1.3［15］由公理（Ł1）~（Ł4）与推理规则MP构成的公理系统记作Ł′。以下公式是系统Ł′中的定理：

ⅰ）A→((A→B)→B)；

ⅱ）(A→(B→C))→(B→(A→C))；

ⅲ）A→A；

ⅳ）0→A；

ⅴ）¬¬A→A；

ⅵ）(A→¬B)→(B→¬A)；

ⅶ）A→¬¬A。

定义1.4［15］在Ł′中，按如下形式引入新的联结词，∧，∨和：

2 公理化真度的计算方法

下面的研究均在Ф中展开，即A，B，C均为不含函数符号的闭公式。

定理2.1设A，B是Łukasiewicz中的公式，则有

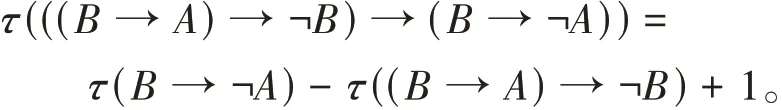
证明首证(B→¬A)→((B→A)→¬B)是定理：

由命题1.3的ⅰ）得├A→((A→B)→B)，├¬A→((¬A→¬B)→¬B)；

由（BL2）得├¬(A&B)→((¬A→¬B)→¬B)；

由（BL3）得├¬(B&A)→((¬A→¬B)→¬B)；

由命题1.2的ⅱ）、ⅲ）得

再证τ(((B→A)→¬B)→(B→¬A))=

由（K2）知

由命题1.1的ⅲ）知

由（K4）知

即τ(((B→A)→¬B)→(B→¬A))=τ(B→¬A)-τ((B→A)→¬B)+1。得证。

例2.1：求命题1.2的ⅳ）((A→B)→B)→((B→A)→A)中τ(((B→A)→A)→((A→B)→B))的值。

解由命题1.2的ⅳ）知（（A→B）→B）→（（B→A）→A）是定理。

由（K2）得

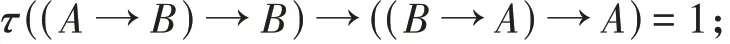
由（K4）得

即τ(((B→A)→A)→((A→B)→B))=τ((A→B)→B)-τ((B→A)→A)+1。

由定义1.4得τ((A→B)→B)=τ(A∨B)；

同理τ((B→A)→A)=τ(B∨A)。

由命题1.1的ⅶ）得

同理τ(B∨A)=τ(B)+τ(A)-τ(B∧A)。

所以

定理2.2设A，B，C是Łukasiewicz中的公式，则有

证明首证(¬B→(C→A))→(¬A→(C→B))是定理：

由命题1.3的ⅱ）得├（A→（B→C））→（B→（A→C）），├(¬A→(¬B→¬C))→(¬B→(¬A→¬C))；

由（Ł3）得

由命题1.2的ⅲ）得├((C&¬B)→A)→((C&¬A)→B)；

由（BL3）得├（（¬B&C）→A）→（（¬A&C）→B）；

由（BL5b）得├(¬B→(C→A))→(¬A→(C→B))。

再证τ(¬B→(C→A))≤(¬A→(C→B))：

由（K2）得τ(¬B→(C→A))→(¬A→(C→B))=1；

由命题1.1的ⅲ）得

定理2.3若A→B为定理，当τ(A)≥a，τ(B→A)≤b时，τ(B)≥a-b+1。

证明由（K2）得τ(A→B)=1；

由（K4）得

τ(A→B)+τ(A)=τ(B→A)+τ(B)；

则τ(B)=τ(A)-τ(B→A)+τ(A→B)≥a-b+1。

例2.2设A，B，C是Łukasiewicz中的公式，则有τ(B→(A→C))≥a-b+1。

证明由命题1.3的ⅱ）知(A→(B→C))→(B→(A→C))为定理。

由（K2）得

由（K4）得

则τ(B→(A→C))=τ(A→(B→C))-τ((B→(A→C))→(A→(B→C)))+τ((A→(B→C))→(B→(A→C)))。

若τ(A→(B→C))≥a，τ((B→(A→C))→(A→(B→C)))≤b，

则τ(B→(A→C))≥a-b+1。

3 结语

本文根据王国俊提出的Ф中公理化真度定义和真度映射τ具有的性质，对谓词逻辑系统Ł∀几类特殊公式的真度计算方法进行了研究，将复杂公式的真度转换为几个简单公式的真度进行运算。后续值得关注的研究内容是公式的相似度、伪距离以及相容度的运算性质。