通过奇偶谐波谱标定线性不对称分子的取向度

李雁鹏，于术娟，郝刚领

（延安大学物理与电子信息学院，陕西 延安 716000）

通常情况下，气体分子在空间中的分布是各向同性的，但是分子本身是各向异性的，这在很多实际应用中都是不利的，分子准直就是为了改变这一事实而提出来的，所谓“分子准直”就是分子轴相对于空间参考系的某一固定轴是平行的，而分子准直技术就是使分子实现分子准直的技术。近年来，激光诱导的分子准直技术引起了人们极大的兴趣［1］，分子准直技术在化学反应动力学［2-3］、高次谐波光谱学［4-5］的纳米级处理［6-7］及激光诱导的电子衍射成像［8-9］等方面具有广泛的应用。扩展这些应用到极性分子，除了需要考虑极性分子的准直外，还需考虑分子的取向，用以区分分子的头部和尾部，所谓“分子取向”就是分子轴相对于固定参考系有唯一指向性。人们一直致力于发展分子取向技术，但分子取向技术的发展比分子准直技术更加困难，因此在分子取向技术方面付出了很大的努力。

然而，随着分子取向技术的巨大进步，在对取向相关的实验结果进行定量分析之前，还需要解决一个难题，即对取向程度（取向度）在实验上实现标定。由于取向是电离损耗［10］和超极化［11］复杂相互作用的结果，目前精确计算取向度是一项重大挑战［12］，通常是间接评估的。目前标定取向度的方案包括以下几种：1）库仑爆炸成像法［13-14］，该方法的弊端是存在假设，即假设碎片离子的发射方向反映了靶离解前分子轴的方向；2）自由感应衰减法［15-16］，该方法的弊端是自由感应衰减与取向度不成正比，而是与时间导数成正比；3）偶奇率［17］（偶次谐波产量与奇次谐波产量之间的比率）已在不对称分子取向度的标定方面得到广泛应用，但通过偶奇率标定取向度时未考虑干涉效应的影响；4）理论谐波谱与实验谐波谱比较的方法［12］，但这种方法需要同时计算谐波产量和准直分布。

因此，直接标定取向度的新方案被提出，通过对二维线性不对称分子HeH2+和H2+3的含时薛定谔方程的数值求解及解析方法分析，证明了奇偶谐波的产量强烈依赖于不对称分子的结构和取向度。在考虑分子的偶奇率和分子结构的情况下，提出一种简单的标定取向度的方案，通过该方案可高精度地标定了线性不对称分子HeH2+和H2+3的取向度，且不需要求解转动方程。

1 解析方法

已有研究表明，对于缺乏反转对称性的分子，奇偶谐波谱的干涉项部分与相应的跃迁偶极矩之间存在着密切的关系［18-19］：

式中，θ是激光场和分子轴之间的夹角，a(ω)是连续态电子的谱振幅，且对θ不灵敏。

现在，考虑取向效应，如文献［20-21］所述，假设分子完全准直且仅部分取向（nu表示分子指向上，nd表示分子指向下），因此有

在不完全取向的情况下，是奇次（偶次）谐波谱且

式中，跃迁偶极矩Du(d)与向上（向下）分子的完美取向有关。由于对称性，可得Ddodd=Duodd及，因此有

当取向度被定义为η=(nu-nd)/(nu+nd)时，有

其中，ζ是偶奇率，在目前的实验中，可以通过偶奇率得到非常粗略的取向度估计。当忽略所有分子特定量，如光谱振幅、返回偶极矩等时，该比率与取向度η2的平方成正比。值得注意的是，在式（5）中，发现取向度不仅与偶奇率密切相关，还与分子内干涉效应密切相关。因此有必要对现有方案进行深入分析，探讨干涉效应对取向度校准结果的影响。

2 数值方法

下面，将上述方案应用到线性不对称分子HeH2+和H2+3中，HeH2+和H2+3分子分别是最简单的线性双核和三核不对称分子，它们可以作为复杂线性分子的基准。线性不对称分子HeH2+和H2+3的哈密顿是H(t)=p22+V(r)+r⋅E(t)，假设分子轴位于X O Y平面，对于线性不对称分子HeH2+的分子势为Z1和Z2为有效电荷。对于线性不对称分子H2+3的分子势为，这里Z为获得所需基态能量的有效电荷，R1、R2及R3是原点和3个核之间的矢量，如图1所示。为了进行比较，将软心参数ξ=0.5用于研究所有线性分子的情况。E(t)=e E(t)是外电场，e是沿着平行于X轴方向的单位矢量，这里E(t)=f(t)εsinω0t，ω0是激光频率，f(t)是包络函数，ε是与峰值激光强度I相关的激光振幅。采用的空间格点是L x×L y=409.6×102.4 a.u.，总持续时间为10个激光周期的梯形脉冲，其中3个激光周期是线性上升的。通过谱方法数值求解含时薛定谔方程H(t)Ψ(t)，一旦得到含时薛定谔方程波函数Ψ(t)，就可以通过下式计算与激光偏振方向平行的高次谐波谱的干涉项［22］：

图1 H 2+3的分子几何与坐标系统缩略图

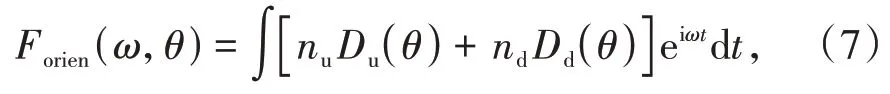
式中，Du(d)是与分子指向上（下）的情况相关的偶极矩加速度。

3 数值结果和讨论

将上述方案应用到线性不对称分子HeH2+和H2+3中。图2A、2B和图3A、3B给出了不同取向度下线性不对称分子HeH2+和H2+3沿激光偏振方向发射的一些典型谐波谱。为了比较，分别用实线和虚线绘制了奇偶谐波谱，从图2和图3可以看出，奇次谐波的产量对分子的取向度不敏感，而偶次谐波的产量对取向度敏感，并随着取向度的增加而增加，导致不同取向度下奇偶谐波的相对产量不同，如图2A和2B所示。然而，谐波谱和相应跃迁偶极矩之间的进一步比较表明，图2A和2B中不同取向度下奇偶谐波的相对产量与图2C和2D中相关偶极矩的预测一致，如公式（4）所述。然而，奇偶谐波谱和对应偶极矩之间仍然存在明显的差异，对于不对称分子HeH2+和H2+3，对奇次谐波的释放起作用的2条高次谐波路径为Logg和Louu。总的来说，在大部分能量区域的奇次谐波释放中第一条路径Logg占主导地位，然而，在双中心干涉效应起重要作用的特定能量区域，第一条路径Logg被显著抑制，在这种情况下，第二条路径Louu在谐波释放中的作用尤为显著，导致Logg这条路径上的干涉最小值被第二条路径Louu的贡献所掩盖，因此，不对称分子的高次谐波谱通常不会显示干涉诱导的显著最小值。然而，只有一条路径Logg贡献到奇次跃迁偶极矩上，因此奇次跃迁偶极矩显示出一个由双中心干涉效应［18，22］引起的显著极小值。当通过公式（5）标定取向度η值时，考虑到多通道的贡献，通过高斯拟合对奇次跃迁偶极矩进行修正，从而消除跃迁偶极矩上的干涉最小，黑色的虚线是通过高斯拟合得到的修正奇次偶极矩，这里偶极矩中的干涉最小值被消除。如图2C、2D和图3C、3D所示。

图2 HeH2+在取向角30°时奇偶谐波谱及偶极矩的比较

图3 H 2+3在取向角30°时奇偶谐波谱及偶极矩的比较

利用奇偶高次谐波谱和修正过的跃迁偶极矩，通过公式（5）标定了线性不对称分子HeH2+和三核分子H2+3的取向度（实心符号曲线）。对于谐波谱的每种情况，由公式（5）计算的η是对整个高次谐波产生平台上的谐波取平均值。相关结果如图4和图5所示，结果表明：同通过偶奇率计算得到的取向度（空心符号曲线）相比，由公式（5）（实心符号曲线）标定的取向度与精确取向度（灰色虚线）非常吻合；在奇偶谐波相对产量相当的情况下，通过偶奇率得到的取向度与精确取向度更接近，如文献［21，23］中通过偶奇率标定CO分子的取向度。当释放的偶次谐波强度大于（小于）奇次谐波时，通过偶奇率ς标定的取向度η值过高（过低），这里采用的表达式为η2=ς，并且省略了跃迁偶极矩的影响。这些现象表明，线性不对称分子HeH2+和三核分子H2+3的取向度不仅与偶奇率密切相关，而且与分子内干涉效应密切相关。

图4 HeH2+取向度的比较

图5 H2+3取向度的比较

4 结论

综上所述，通过奇偶高次谐波产生标定了不对称线性分子的取向度，此方案充分考虑分子结构的影响，此方案可应用于双核线性不对称分子HeH2+和三核线性不对称分子H2+3，且无需求解二维含时薛定谔方程。并且充分讨论了偶次谐波与奇次谐波的相对产量在不同的情况下，通过何种方法标定的取向度更接近精确的结果。在光化学和阿秒科学中，由于取向度在许多取向相关的过程中起着重要作用，此工作为相关实验提供了建议。