具有S U（1，1）李代数结构的广义谐振子系统精确求解

李 伟，曹冰冰，郝刚领

（延安大学物理与电子信息学院，陕西延安 716000）

实现超快且高保真度量子调控的一个基本要素是精确设计脉冲或脉冲序列驱动的人造量子系统，控制系统的非绝热动力学演化从而实现量子态的制备、转移和多通道跃迁等任务。其相关的应用涵盖了光致化学反应［1］、原子与分子碰撞动力学［2-3］和量子模拟与量子信息处理［4-6］等方面。为了实现量子调控在这些方面的应用，前提之一是对外场驱动的含时量子系统的演化进行精确求解，以此设计脉冲或脉冲序列强度以及其与系统相互作用的时间。含时量子系统的精确求解长期以来是量子理论的一项重要但未有效解决的课题。在具体的研究过程中，人们通常利用绝热近似方法来处理这类问题。绝热近似方法基于量子绝热定理［7］（能级没有简并的量子体系，如果初态制备在含时哈密顿量的某一个瞬时本征态上，当调控系统的演化足够缓慢时，此后任意时刻系统都将沿着哈密顿量的这一本征态演化），可实现系统沿着相应绝热通道高保真度的量子调控。但绝热近似方法的不足在于演化速度缓慢，容易受到环境诱导的退相干的影响。这促使含时量子系统的非绝热动力学研究引起了人们的普遍关注并取得了较快的发展。

外场驱动的n能级量子体系求解的一个常见思路是首先将薛定谔方程中的波函数和哈密顿量分别用n阶列向量和n阶矩阵表示，其次将其转化为有n个变量的一阶变系数线性常微分方程组或者联立这些方程建立关于某个变量的n阶微分方程，最后再利用解的结构和性质，寻找方程的解析解或特殊函数解。该方法仅能找到部分非平庸两能级和非常有限的三能级模型的解析解，如Landau-Zener模 型［8-9］、Allen-Eberly模 型［10-11］、Bambini-Berman模型［12］、Carrol-Hioe模型［13］和Demkov-Kunike模型［14-16］等，很难将其推广到三能级以上甚至是无穷维量子体系的求解。为了克服这一不足，LEWIS和RIESENFELD提出了动力学不变量算子方法［17-18］：用包含不变量算子在内的一组守恒量完全集的本征态刻画系统演化的波函数。不变量算子方法摒弃了用非守恒的哈密顿量的本征态近似描述系统的演化，使得含时量子系统可以严格求解。然而什么样的系统存在不变量算子以及如何寻找不变量算子，到目前为止仍然是一个亟待解决的课题。与此相关的另一个重要方法，是由WANG等提出的代数动力学方法［19-21］。代数动力学方法原则上可以用来求解具有诸如SU（2）、SU（1，1）等具有半单李代数结构的含时量子体系，其核心在于通过引入包含相应李代数生成元的正则变换，将薛定谔表象变换到规范表象中，使规范表象中的有效哈密顿量仅含有Cartan算子，从而可以严格求解。代数动力学方法的显著优点是一旦找到规范变换，就可以得到系统的不变量算子。但要确定正则变换中控制参数所满足的函数，就需要求解非线性方程组，之前仅有少数例子通过这种方法得到解析解［22］。

本文受代数动力学方法［19-21］的启发，通过选择合适的正则变换建立薛定谔表象和规范表象之间哈密顿量所满足的关系，并通过解析求解，得到了描述具有SU（1，1）李代数结构的广义谐振子量子系统演化的波函数。

1 利用表象变换构建两表象中的哈密顿量

微观粒子在Pauli阱［23］中的运动可以用广义谐振子模型［24-25］来描述，其哈密顿量可以表示为

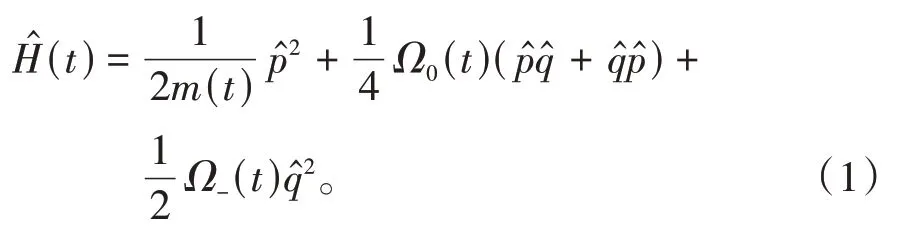
方程（1）中第①项是依赖于随时间变化的等效质量m(t)的动能项；第②项是与粒子速度有关的广义势能项；第③项是谐振子势能项，其中系数Ω-(t)用来刻画谐振子的刚度。为了说明系统具有的李代数对称性，引入算符

将方程（1）改写为

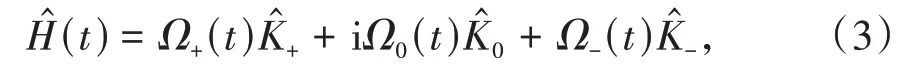
为了研究系统的非绝热演化，即确定系统在任意时刻的波函数，需要求解薛定谔方程

值得注意的是，对任意给定的外场（通过哈密顿量̂(t)中的脉冲参数Ω+(t)，Ω0(t)和Ω-(t)来描述），人们很难解析求解出波函数考虑到系统具有的S U（1，1）对称性，研究的出发点是利用基于S U（1，1）李代数的代数动力学方法，寻找具有特定函数形式的控制参数，使得薛定谔方程（5）严格可解。为了实现这一目标，通过引入规范变换

将薛定谔表象变换到规范表象中，在规范表象中的有效哈密顿量满足新的薛定谔方程：

相应的，通过将式（5）（6）代入到薛定谔方程（7），可以计算得到有效哈密顿量

可以看出，由于幺正算符̂(t)选择的多样性，有效哈密顿量存在无穷多种可能的结果。但选取的一定要形式简单，使得通过方程（6）和方程（7）容易求出系统的波函数为了方便起见，取

其中，控制参数θ(t)和φ(t)均为与时间有关的实控制参数。相应的，将方程（9）代入方程（8），容易得到在规范表象中的有效哈密顿量

其各生成元的系数为

需要说明的是，为了表示方便，上面各式中省略了各个函数的自变量t。可以看出，̂(t)通过含时 脉 冲 参 数{Ω+(t)，Ω0(t)，Ω-(t)}和 控 制 参 数{θ(t)，φ(t)}来调控。为了选取的表达式简单，令

其中，κ是与时间无关的常数。将方程（12）代入到方程（11a）、（11b）、（11c），得到脉冲参数满足的方程

方程（13）为一阶线性常微分方程，方程的解可以一般的表示为

这里的θ(t0)为参数θ(t)在系统演化初始时刻t=t0时的取值。进一步，将方程（15）代入到（14）并整理得

总的来说，任意给定与时间有关的实脉冲Ω+(t)和Ω0(t)，通过方程（16）可以确定脉冲参数Ω-(t)，进而完全得到外场驱动下系统哈密顿量（1）的表达式。在下一节中，将通过解析求解得到满足方程（1）和方程（16）的驱动系统的波函数。

2 薛定谔方程求解

首先求解规范表象中的薛定谔方程（7），将方程（2）、（12）代入到方程（10）中，有效哈密顿量可以改写为

可以看出，在不考虑上式右边随时间变化的系数时，整个哈密顿量为标准的量子谐振子模型，受此启发，引入哈密顿量

其满足本征方程

这里哈密顿量对应于本征值

的本征函数为

此时将（22）式和（23）式代入到薛定谔方程（7），整理后可以得到关于变量t满足的一阶线性微分方程

很容易得到该方程的解为

结合式（21）和（25），在规范表象中薛定谔方程（7）的基本解可以直接由

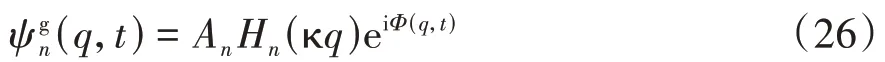
接下来通过求解薛定谔方程（5）得到系统的波函数。由正则变换式（9）可知，薛定谔表象中的基本解ψn(q，t)可以通过规范表象中的波函数ψgn(q，t)表示，即

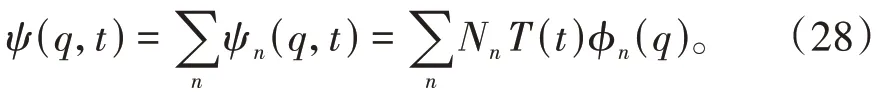
至此通过求解广义谐振子所满足的薛定谔方程得到了系统演化的波函数。

3 结论

总的来说，本文基于广义谐振子系统具有的SU（1，1）对称性，通过引入SU（1，1）规范变换，建立了薛定谔表象和规范表象中哈密顿算符的对应关系，并通过调控规范变换中的参数得到外场的解析表达形式。在此基础上，利用两表象中波函数的变换关系，得到了系统演化的波函数。利用本文得到的解析解可进一步用于研究诸如离子阱中的粒子等具体的量子系统的动力学行为，为广义谐振子系统量子调控的实验实现提供了理论依据。此外，本研究方法有望进一步推广到具有其他半单李代数结构的量子系统中。