对近阈谐波短轨道抑制作为隧穿出口标志的检验

于术娟，李雁鹏，刘竹琴，郝刚领

（延安大学物理与电子信息学院，陕西 延安 716000）

隧穿是量子力学中最基本的现象之一［1-2］，激光诱导的隧穿电离［3］常被认为是许多强场过程的第一步，如高次谐波产生［4-5］和阈上电离［6］。近年来，随着测量技术的发展，人们可以利用这些与隧穿相关的过程作为研究隧穿的时间特性的工具，即前所未有的时间（阿秒）分辨率［7］。例如，利用椭圆偏振激光场中的阈上电离光电子动量分布来研究隧穿时间［8］（电子通过由激光场和库仑势形成的势垒所花费的时间）、出口处的瞬时动量［9］等；用正交偏振双色激光场的高次谐波谱研究了电离时间［10-11］（即隧穿电子离开势垒的时间）。

为了理解隧穿，除了与时间相关的量外，与空间相关的量也很重要，例如隧穿出口，其与隧穿时间和电离时间相比，直接与靶的有效势相关［12］，并对阈上电离光电子动量分布有重要影响。将实验和理论的阈上电离结果进行比较，可推导出隧穿几何［13］。而隧穿出口导致高次谐波截止能量从经典预测的3.17Up+Ip增加到量子预测的3.17Up+1.32Ip，0.32Ip这个差值反映了散射电子从隧穿出口到原点获得的能量（Ip为电离能，Up=E02/4ω02为制动能，E0为激光振幅，ω0为激光频率）；同时列文斯坦模型通过相关的虚部包含了非零隧穿出口，并对列文斯坦振幅进行鞍点分析，从而推导出3.17Up+1.32Ip这个截止规律，且可追踪到非零隧穿出口。当再散射电子从隧穿出口到达原点时，获得额外的能量0.32Ip，由于实验中激光强度的不确定性，0.32Ip这个额外增加的能量在实验中不易识别。并且隧穿出口也会影响高次谐波量子轨道的电离和返回时间［14-15］。其中量子轨道包括长电子轨道、短电子轨道及再散射电子在激光场中不同漂移时间的多次返回［16-17］，这些轨道对高次谐波的贡献可通过传播效应［18］进行调制。因此，只能通过测量高次谐波轨道的电离时间和返回时间来间接研究隧穿出口。但是这只是间接测量，在实验上不能直接观测谐波的电离和返回时间，这些是隧穿位置对阈上谐波的影响。

在近阈和阈下谐波的研究中，最近的研究［19-20］表明，列文斯坦模型在谐波释放的描述中，忽略了束缚-束缚跃迁和连续-连续跃迁等多光子过程。此外，阈附近的电子受到库仑力的作用，库仑修正的量子轨道包括长轨道、多次返回轨道及与隧穿相关的轨道，这些轨道对阈附近或阈以下谐波的产生有重要影响。然而，很少有研究关注短轨道对近阈或阈下谐波的贡献。本文报道了一个与短电子轨道高次谐波产生有关的现象，该现象可直接用于隧穿出口的研究，通过含时薛定谔方程的数值解，研究了具有不同电离能原子的高次谐波产生。应用数值方案，从全轨道含时薛定谔方程结果中挑选出短轨道对高阶谐波的贡献。对于较长的激光波长和较低的激光强度，多光子过程的影响很弱，计算得到的短轨道高次谐波谱在阈值附近有一个能量区，在该区域谐波释放被显著抑制；且能量区域的宽度由靶体的电离能决定。但考虑了长短电子轨道的所有贡献后，在含时薛定谔方程模拟中，这个能量抑制区域消失了，此现象归因于隧穿出口对短轨道的影响，从而为研究隧穿的空间特性提供了一个可能的观测对象，并对近阈谐波短轨道抑制作为隧穿出口的标志进行了检验。

1 数值方法

这里研究的模型原子的哈密顿为H(t)=p2/2+V(r)+r⋅E(t)（采用的是原子单位ℏ=e=me=1），式中为用于避免库仑奇异性的平滑参数，ρ为用来控制库仑势范围的屏蔽参数；Z为有效电荷，用来调整模型原子的电离能与真实原子的电离能相匹配（对于Mg+的电离能Ip=4 a.u.；对于Li2+的电离能Ip=4.5 a.u.），例如，ξ=0.073及ρ=0，Z=1.512重现了Li2+的电离能Ip=4.5 a.u.，振幅为E0及频率为ω0的外电场是E(t)=e x f(t)E0sinω0t，其中f(t)是包络函数，e x是激光电场方向的单位向量。计算中采用了10周期的激光脉冲，其中3个周期是线性上升的，另外7个激光周期保持一个常数不变。由于脉冲不是很短，计算结果对脉冲包络不敏感。含时薛定谔方程是通过谱方法数值求解的［21］，这里采用的空间步长为Δx=Δy=0.1 a.u.，且时间步长小于0.1 a.u.，每个时间步长后，x和y的每个维度的含时薛定谔方程的波函数都需要乘上一个窗函数，用来吸收边界处的连续态的波包。沿着x轴的窗函数有如下形式：当|x|≤x0时，F(x)=1；而当|x|≥x0时，F(x)=cos18[π( ||x-x0)(L x-2x0)]；对于全模拟，x0=L x/8作为沿着x轴方向吸收方案的边界，相似的处理也在y轴采用了。由于与短电子轨道和长电子轨道相关的再散射电子具有经典三步模型所预测的不同的最大位移，可通过在不同空间位置的吸收边界处放置窗函数来分离期望轨道的贡献［22-23］，或者，对于目前的情况，在设定xb=0.9xq和保持yb=L y/8不变的情况下，得到了剔除长轨道和多次返回对高次谐波的贡献，从而获得了短轨道的含时薛定谔方程结果，式中xq=E0/ω20为经典电子在激光场中的颤动振幅，其接近短轨道的最大位移。对于全模拟，空间格点为L x×L y=409.6×102.4 a.u.，足以得到收敛的结果。对于短轨道模拟，空间格点为L x×L y=204.8×102.4 a.u.，一旦获得与全模拟相关的含时薛定谔方程的波函数ψf(t)及与短轨道模拟有关的波函数ψs(t)。通过偶极子加速度的傅里叶变换，即可计算整个高次谐波频谱和短轨道高次谐波谱。

2 结果和讨论

首先，考虑长程势的结果ρ=0，专注于短轨道模拟，图1和图2绘制了不同激光参数下Mg+和Li2+的短轨道高次谐波谱，为清楚起见，此处仅绘制奇次谐波谱的结果（文中其他图的情况类似）。对于每个离子，以2种方式呈现；图1A和图2A通过改变激光波长并固定激光强度来实现，对于图1B和图2B的情况则相反。

在本研究中，原始数据显示，在更高的激光强度下，高次谐波谱的产量也更高。然而，不同激光强度的谐波谱曲线在同一面板中会发生重叠，特别是在阈值附近，这样一来，这些曲线很难被区分开。为了进行比较，将图1B和图2B中激光强度相对强的曲线向下平移，其中，激光强度最强曲线的垂直移动比例因子是最大。

对于图1A中I=4×1016W/cm2的Mg+，随着激光波长的增大，高次谐波产量显著降低。特别是，接近阈值的谐波的产量下降更快，频谱显示出显著抑制的能量区域，能量从Ip扩展到2Ip左右；在该区域以外，高次谐波产量单调增加；相对于其他波长，这种抑制现象在λ=500 nm时最明显。当激光波长为λ=400 nm，随着激光强度增加，高次谐波谱中的抑制现象会减弱，这种抑制在较低的激光强度下变得更加明显，如图1B所示。对于Ip较大的Li2+，观察到类似的现象，如图2所示。对于较低的激光强度和较长的激光波长，Li2+的短轨道高次谐波谱也显示出一个明显的抑制区域，该区域大约也位于Ip到2Ip左右。

图1 不同激光强度和波长下Mg+短轨道高次谐波谱的比较

图2 不同激光强度和波长下Li2+短轨道高次谐波谱的比较

需要强调的是，在全轨道含时薛定谔方程模拟中，短轨道谐波在阈值附近的强抑制现象消失了。之前的研究［24-25］表明，对于接近阈值的谐波，多次返回对高谐波有重要贡献，图3A中全轨道谐波频谱显示出高强度［22-23］，短轨道结果却在阈值附近展示了抑制现象；相比之下，对于全轨道的含时薛定谔方程结果，阈值附近的谐波产量明显高于截止位置附近的谐波产量，因此，阈值附近的抑制是不存在的。由于不同轨道之间的干涉，全轨道高次谐波结果的时频分析显示了一些复杂结构，而短轨道谐波的时频分析却清楚地展示了质动能电子Ep=ω-Ip＜Up的抑制现象，如图3B所示。图3B中的黑色实线显示了再散射电子首次返回核心的电子轨迹，该轨迹是通过修正的经典三步模型获得的，而三步模型考虑了隧穿出口；在该模型中，电子在t时刻的位移x(t)为

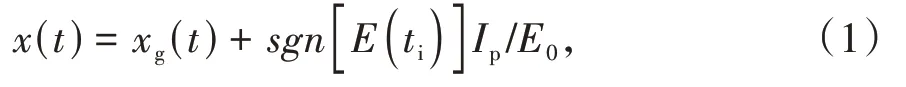
式中，xg(t)是一般三步模型的位移，ti是电离时间，Ip/E0给出了隧穿出口的粗略估计。对于图3中所采用的激光参数，可得Ip/E0≃4.35 a.u.，总体上，在不同激光参数下，近似表达式Ip/E0对隧穿出口的估计同样成立。经典的短轨迹预测（实心黑色曲线中具有正斜率的分支）显示了最小的返回能量Emin≈0.13Up≈0.56Ip，通过垂直箭头表示，意味着能量低于Hmin=Emin+Ip的谐波被经典禁戒，与含时薛定谔方程的结果一致；这种禁戒不会在长轨道中发生，正如图3B中实心黑色曲线中具有负斜率的分支所示。在不考虑隧穿出口的情况下，一般经典模型的预测也不存在禁戒，如灰色实线所示。需要注意的是，一般经典模型的预测与含时薛定谔方程的时频分布有着显著差异。当再散射电子以零速度出现在激光场中，从隧穿出口点x0到达原点（核心位置）时，获得了沿短轨道的最小返回能量Emin；在此过程中，再散射电子被激光场加速，获得能量Emin，图3C展示了这个过程。相比之下，再散射电子沿着长轨道运动接近核心时，会被激光场减速，这种减速机制允许长轨道电子获得接近于零的返回能量。

阈值附近短轨道谐波的禁戒也可通过列文斯坦模型中的量子轨道理论来理解，图3D绘制了Li2+的隧穿位置和短轨道的振幅，以谐波能量为函数，通过量子轨道理论计算，隧穿位置|x0|最大值为Hmin=8.2 a.u.（大约2Ip）。众所周知，对于能量较低的谐波，短轨道电子的电离时间ti更接近于零场，给出了隧穿位置的半经典估计|x0|≈Ip/|E(ti)|，因此，隧穿位置|x0|应大于能量低于Hmin=8.2 a.u.的短轨道谐波，这一现象是在图3D中观察不到的情况。而通过e b（b是相关轨道上准经典作用的虚部，只考虑b的负值）计算的短轨道的振幅反映了半经典预测和量子预测之间的不一致；且能量低于Hmin=8.2 a.u.的轨道振幅下降非常快，这意味着相关短轨道谐波的产量也非常低，对应于最大隧穿位置|x0|的能量Hmin可认为是短轨道电子在量子轨道理论中贡献的最小谐波能量。在不同情况下，量子轨道理论计算出的Hmin值约为2Ip，与修正的半经典三步模型的预测值相近。上述讨论解释了图1中短轨道抑制现象的起源，并将显著抑制区域与最大隧穿位置|x0|联系起来。

图3 Li2+高次谐波波谱比较、时频分布、高次谐波的产生及电子隧穿位置和振幅

接下来，图4探讨了图1中阈值附近抑制现象对激光参数依赖的潜在机制。如图1所示，这种抑制现象对于较低的激光强度和较长的激光波长更为显著，在此情况下，多光子过程发挥的作用更小。因此，只有当多光子过程对高次谐波的影响不强时，才会出现短轨道抑制现象。实际上，最近的研究表明，对于阈值附近的谐波，除了与隧穿相关的再散射量子轨道外，束缚-束缚跃迁这样的多光子过程也在高次谐波产生中起着重要作用；这些过程发生在核附近，且在目前的短轨道吸收方案中幸存下来，结果表明，多光子过程的贡献可以覆盖短轨道谐波谱中出现的显著抑制区域。对于较低的激光强度和较长的激光波长，束缚-束缚跃迁更难发生，且隧穿过程占主导地位，因此短轨道谐波谱展示了明显的抑制区，为了验证这一猜想，对短程势的原子进行了模拟，短程势的特点为基态和激发态之间的能级间隔很大，相应的跃变也较难发生。相关结果如图4所示，在不同屏蔽参数ρ值下，绘制了Li2+的高次谐波谱的对比。对于ρ=0的情况，激光强度I=5×1016W/cm2及波长为200 nm的谐波在阈值附近没有明显的抑制现象，然而随着屏蔽参数ρ的增加，相应的谐波谱在阈值附近展示明显的抑制区域，此抑制区域显示出强烈的振荡，通过水平箭头来表示强振荡的抑制区域，其上边界与量子轨道理论预测的Hmin非常一致，如垂直箭头所示。抑制区域的宽度从Ip扩展到2Ip左右，类似于图1中较低激光强度和较长激光波长的Li2+情况，这种相似性意味着图1和图4中抑制现象的相似起源。Mg+也具有相似的情况，这里就不展示了。

图4 不同ρ下Li2+短轨道高次谐波谱的比较

3 结论

综上所述，通过含时薛定谔方程的数值解，研究了不同电离能原子的高次谐波产生。应用数值方案，从含时薛定谔方程全轨道模拟中挑选出短轨道对高阶谐波的贡献。高阶谐波展示了一个靠近阈值的光谱区域，在该区域，短轨道谐波的释放被显著抑制。对于激光强度较低、激光波长较长、多光子效应较弱的情况，此抑制现象更为显著。此种抑制现象源于隧穿出口对短轨道谐波的影响引起的，该现象可直接用于隧穿出口的研究，其为研究隧穿引发的强场过程提供了新的见解，也为研究隧穿以外的其他强场过程打开了一扇新的机会之窗，同时通过其他原子检验了近阈谐波短轨道抑制现象作为隧穿出口标志的正确性。