基于频繁项统计的流-安时积分SOC估计方法

李 昆，赵 理,2，赵博阳，客汉宸，李俊丽

(1.北京信息科技大学 机电工程学院， 北京 100192；2.北京电动车辆协同创新中心， 北京 100192；3.河北工业大学 人工智能与数据科学学院， 天津 300401)

精确的荷电状态估计(state of charge,SOC)是动力电池系统优化能量管理策略、提高电池安全性和使用寿命的基础[1]。SOC属于间接测量变量，需通过电流、电压等传感器监测数据进行间接估算。例如，开路电压法、内阻法是通过间接参数估计电池荷电状态[2]。然而，电动汽车工况复杂多变，这些间接测量参数变化规律非线性大，仅依赖于这些间接测量参数很难获得精确的估计结果[3]。安时积分法通过计算积累电量来计算剩余容量，是一种简单实用的方法，在电动汽车上得到广泛应用，但其精度受电流传感器及库仑效率影响较大[4]。由于电动车工况复杂，电池容量受温度、充放电倍率等因素影响较大，实现对电池SOC的准确估算一直是国内外学者研究的重点[5]。

徐尖峰等[6]在进行电池SOC估算时使用传统的安时积分法，但其估算过程是开环的，电流积分引起的累积误差会不断增加，从而降低SOC的估算精度。鲍慧等[7]采用开路电压和安时积分相结合的方法，完成了初始SOC的估计及充放电过程中电量的积累，但其使用折算库伦未能有效解决电流差异对库仑效率的影响；吴海东等[8]利用训练后的BP(back propagation)神经网络对库仑效率进行预测，提高了安时积分法进行SOC估算的精度，但是该方法对特定数据集的依赖性较高且需要提前训练；刘东等[9]引入充放电曲线电压拐点来修正安时积分法中的初始荷电状态SOC(t0)，在一定程度上解决了开路电压法需长时间静置问题，但未考虑库仑效率对电池电量损失的影响；丁镇涛等[10]采用安时积分法与无迹卡尔曼滤波结合的方法估算电池SOC，其估计精度相比传统卡尔曼滤波、扩展卡尔曼滤波得到提高，但存在稳定性易受噪声干扰的问题。

分析可见，传统安时积分法是一种开环的估计方法，其误差在电流积分过程中持续积累。电流传感器的精度和元器件老化导致测量值的概念飘移持续影响累积效果。同时，库仑效率受温度、SOC、充放电倍率等因素影响持续变动，极易导致传统安时积分法估算精度下降。

针对此问题，本文提出了一种基于频繁项统计的流-安时积分算法。该算法基于概要数据结构对积累电量进行统计，利用统计后的积累电量动态修正库仑效率，进而保证电池剩余容量的准确估计。仿真和实验表明：该算法能有效减小传统安时积分法产生的累积误差，提高剩余容量及SOC的估计精度。

1 理论基础

1.1 传统安时积分法

安时积分法是当前电动汽车领域常用的动力电池SOC计算方法，通过一段时间内电流的连续积分与额定容量的比值计算电池相对变化电量[11-12]，进而利用初始SOC(t0)计算剩余容量SOC,其数学表示如下：

(1)

式中：CN为额定容量；I为电池电流；η为库仑效率。

通常基于OCV-SOC关系确定初始荷电状态SOC(t0)，额定容量CN可由厂家提供或实验室测量获取，电流值可通过高精度传感器测量获取，但库仑效率η使用常规方法难以准确测量[13]。事实上，库仑效率在多个充放电循环过程中是持续变化的，使用平均值、折算值或估计值代替实际η值估计电池SOC是不准确的。充放电电流、温度、SOC、健康状态(state of health,SOH)等因素都会对库仑效率产生影响。

1.2 放电库仑效率

库仑效率为电池工作时实际放出的电量与充入的电量比值，也称电池的放电效率[1]。库仑效率会影响电池的剩余电量，从而影响对电池SOC的准确估计[14]。

电池以任意电流In放电至截至电压，此时以C/3的倍率充电至SOC值为1，充电容量为QC,C/3=(C/3)tC,C/3,其中tC,C/3是充电时间。经过10 min静置后，电池以任意电流In放电至截至电压，放电容量为Qd,In=(In)td,In,其中td,In是放电时间，故放电库仑效率可计算如下：

(2)

在电池充放电过程中，能量损失是无法避免的。电动车辆工况复杂多变，各因素(电流、温度、容量)都会影响动力电池放电库仑效率[15]。如图1所示，不同温度、SOC、充/放电倍率下电池库仑效率的变化范围非常大。使用平均值、折算值或估计值代替实际η值估计电池SOC很难得到精确解。

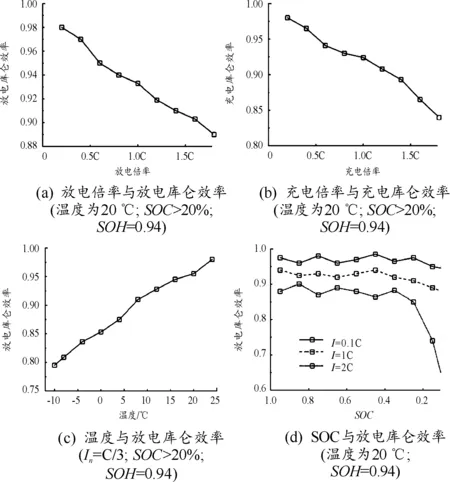
图1 充/放电倍率、温度、SOC对库仑效率的影响曲线

1.3 Lossy Counting算法

Lossy Counting算法是斯坦福大学的Manku和Motwani共同提出的一种基于确定误差参数的算法，用于计算单项事务数据流上的频繁计数。Lossy Counting算法在内存中为出现频次较高的项建立了一个概要数据统计表，对每一个新到的数据项，若概要数据统计表中有对应的项存在，则直接累积。若不存在，则新增加一项。每隔固定间隔更新概要数据统计表，删除其中出现频次较低的项。这样，Lossy Counting算法利用较低的存储空间和计算成本，保证了频繁项统计的精确性。

算法如下：

① 定义并置空数据结构D(e,f,Δ)；

② 读入当前记录e，在D(e,f,Δ)中查找e是否存在？若存在，则将其对应的频率f加1，若不存在，则在数据结构D(e,f,Δ)中新建条目(e，1，bcurrent-1)；

③ 边界判断。当到达桶边界时，对D进行裁剪然后执行②。裁剪规则为：“若条目(e，f，Δ)中f+Δ≤bcurrent，则删除它”。每当用户请求大于阈值s的频繁项列表时，满足(f≥(s-ε)n)的条目被输出。

2 基于Lossy Counting算法的流-安时积分SOC估计算法

2.1 算法流程

基于频繁项统计的流-安时积分法与传统安时积分法的区别在于：在对一段时间内的电流进行连续积分时，将电流按放电倍率大小分割成多个区间，利用频繁项统计技术对不同区间分别进行积累电量统计，最后利用可在线更新的库仑效率修正不同区间得到的积累电量，从而得到更为精确的剩余容量计算结果，如图2所示。

2.2 库仑效率的更新

实际车辆驾驶条件复杂多变，在整个充、放电过程中，很难用式(1)中的估计库仑效率精确计算SOC或可用容量[16]。因此，在每个测量点用精确的库仑效率对电流进行校正，用式(3)代替式(1)可得到较精确的结果。式(3)中I(t)、T(t)、SOC(t)、SOH(t)是电池在时间t时的电流、温度、SOC和SOH。

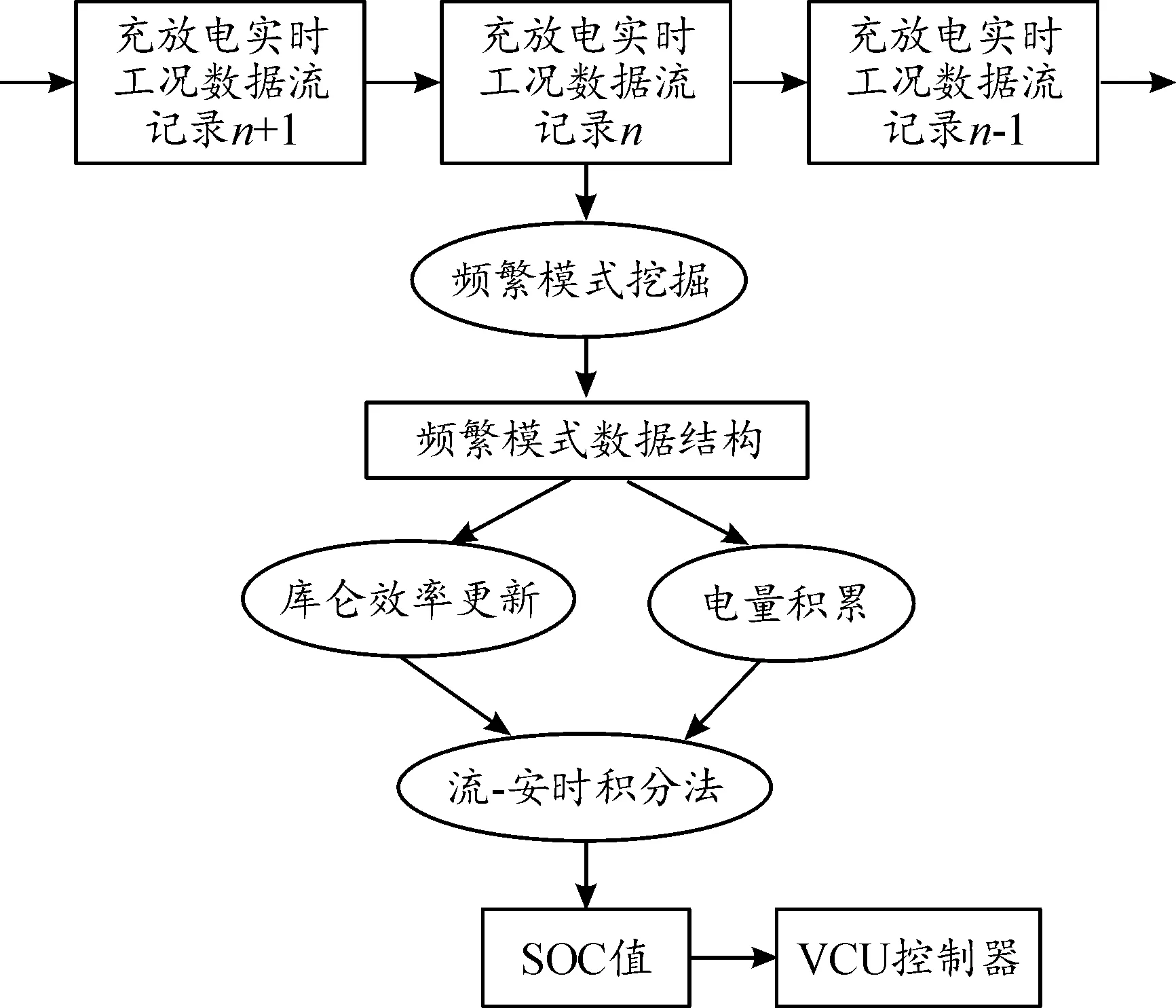
图2 流-安时积分法工作流程框图

(3)

实际上，上位机端在每个离散的时间点tk(tk=Δt×k)接收传感器能发送数据。Δt是采样间隔，k是采样次数。因此:

SOC(t)≈SOC(t0)-

(4)

一般来说，库仑效率η的定义域是连续的，无法在定义域中获得每个点的精确η。我们将连续定义域分成若干大小相同的晶格。在同一晶格中，库仑效率取相同的值。

SOC(t)≈SOC(t0)-

(5)

用“L1、L2、…、Ln”对这些格进行编号，计算电池的SOC，得：

[ηL1×QL1+ηL2×QL2+…+ηLn×QLn]

(6)

ηL1×QL1,K+ηL2×QL2,K+…+ηLn×QLn,K

(7)

实现了k个循环后，可以获得矩阵：

(8)

只要Ln≤k，有许多方法可用来估计未知参数η。本文用最小二乘法估计η，最小平方和为：

(9)

为了解决极值问题，我们可以得到:

j=L1,L2,…,Ln

(10)

这样，库仑效率η可以在运行k(Ln=k)次循环后进行动态更新。事实上，累积容量大部分都集中在几个特殊的格子中，故将库仑效率离散化，用每个晶格的积累电量动态更新库仑效率η就可以精确计算SOC或可用容量。

2.3 电量积累

将接收到的电流记录分成等宽的桶，每个桶的宽度为w=[1/ε]个电流记录。桶的编号记为id，从1开始。当前桶id为bcurrent，其值为N/w，对于一个电流区间e，电流落在该区间的真实频率为fe(从起点到当前记录器)。在这些参数中，N、bcurrent和fe是变量，其值随着电流记录的不断输入而变化。ε和w是不变参数，其值固定。为了计算频率，定义一个数据结构D(e，f，Δ)，其中e是电流区间，f是元素e的频率估计，Δ是f中最大的可能误差。得到的不同电流区间积累电量的数据结构D的过程如图3所示。

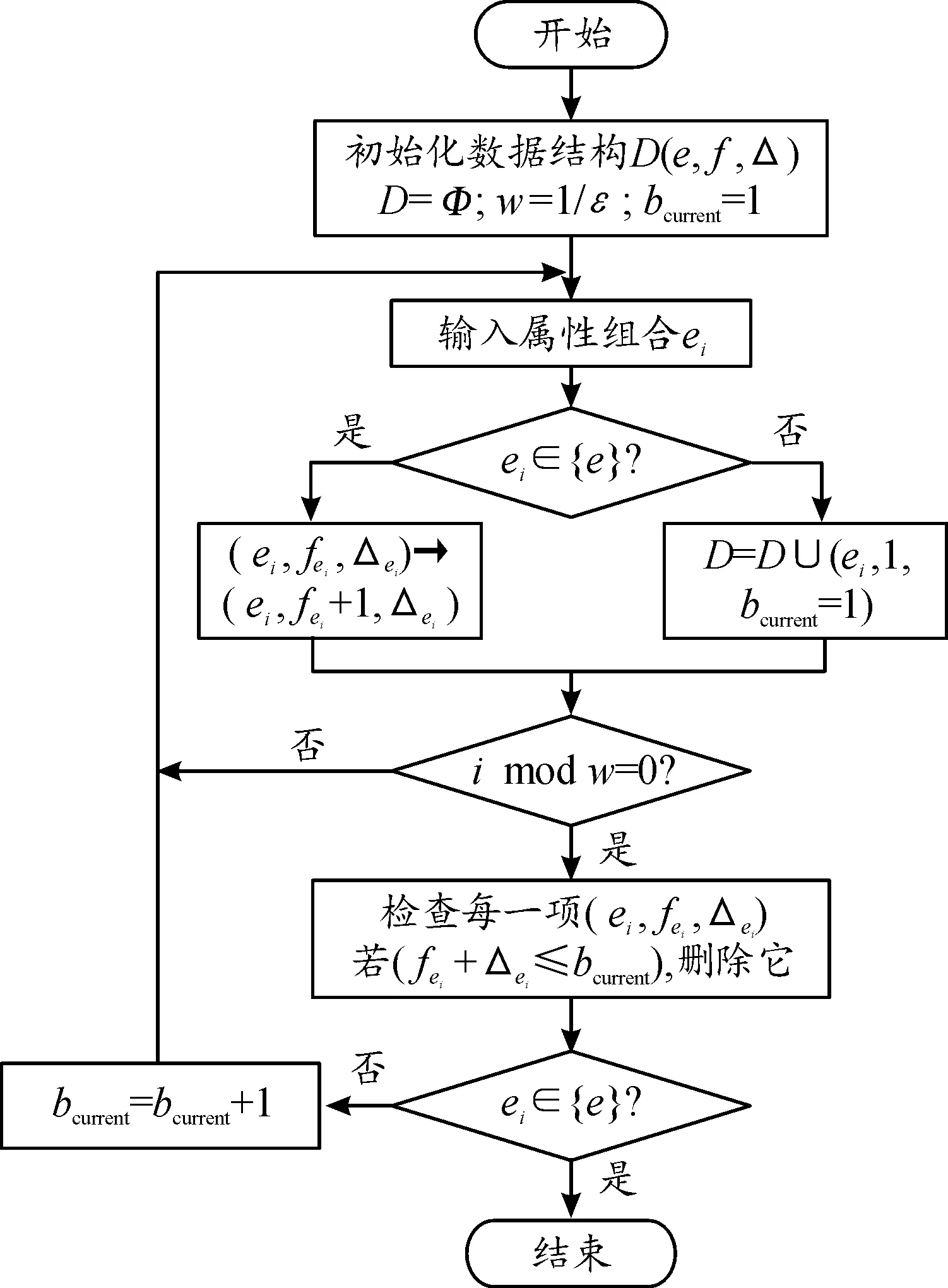
图3 电量积累概要数据结构框图

3 实验分析

3.1 放电顺序对累积电量的影响

为分析放电顺序对累积电量的影响，在室温下，利用以下设备及实验步骤展开实验：① 利用艾德克斯8500+可编程电子负载以0.2 C的倍率对单体NCR18650B电池放电至截至电压2.5 V，静置20 min；② 利用艾德克斯IT6722A可编程电源以1/3 C的倍率对单体电池恒流充电至上截至电压4.2 V,再恒压充电至截至电流0.05 C，静置20 min；③ 利用艾德克斯8500+可编程电子负载对电池单体分别进行95个A循环和B循环放电，结束后静置20 min;④ 以0.2 C放电至截至电压2.5 V；实验环境、A/B循环和测试过程分别如图4-6所示。

放电A循环和B循环步骤如下：A分为10步，分别以0.25 C、0.5 C、0.75 C、1 C、0.75 C、1 C、0.5 C、0.25 C、0.5 C、0.75 C的放电倍率，按6、4、4、6、4、6、4、6、4、4 s的时间间隔放电；B分为7步，分别以1 C、0.75 C、0.5 C、0.25 C、0.5 C、0.75 C、1 C的放电倍率，按6、6、6、12、6、6、6 s的时间间隔放电。A循环和B循环虽然放电顺序不同，但在相同放电倍率下保持总放电时间相等，如图5所示。

图4 实验台架及A循环放电曲线

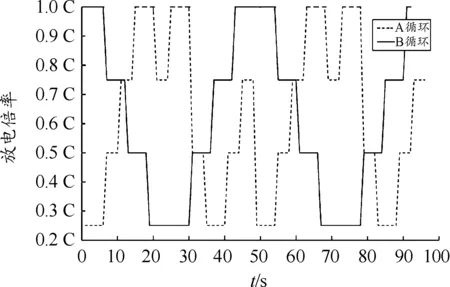
图5 放电A循环和B循环(2个循环)倍率曲线

电池以不同的放电倍率组合放电后，试验数据如图6、表1、表2所示，其放出总电量差别不大。1号电池2种放电循环(A和B)下，放出电量的差距为 3.049 2-3.008 7=0.040 5 AH，2号电池差距为3.037 7-3.018 2=0.019 5 AH,3号电池差距为3.097 2-3.093 7=0.003 5 AH。因此，可认为提出算法的容量积累过程不受电池充放电顺序影响。

图6 95个A循环/B循环和电流以0.2 C放电电压曲线

表1 95个A循环+0.2 C放电数据

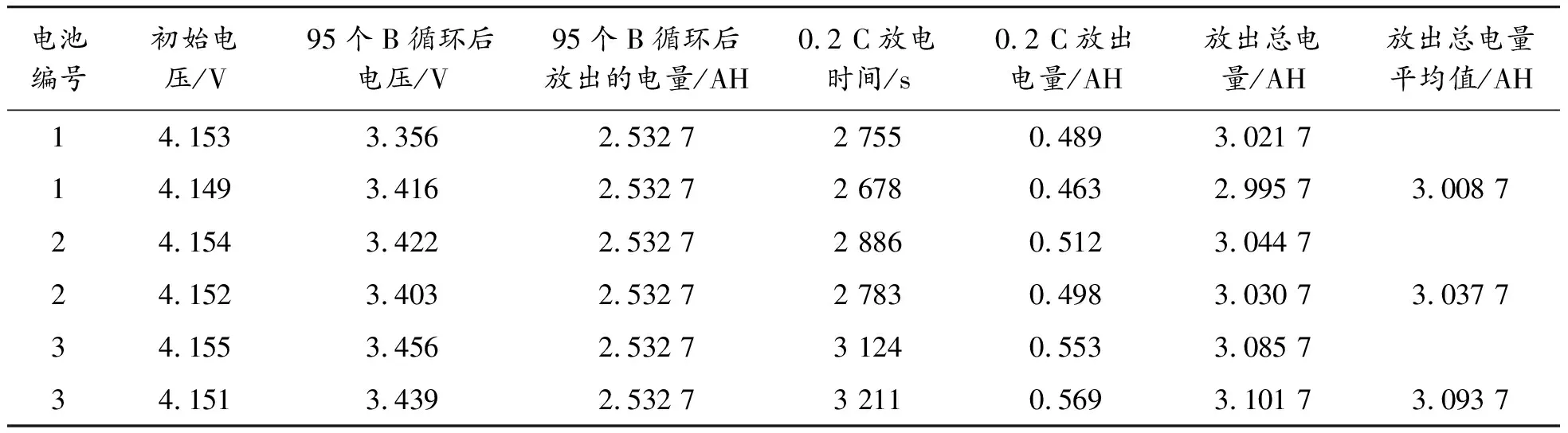
表2 95个B循环+0.2 C放电数据

3.2 UDDS工况下算法对比

利用图7所示测试环境，选择了动态波动较大的城市运行工况UDDS(urban dynamometer driving schedule)对电池单体进行2种算法(所提出算法与传统安时积分法)对比实验，设定温度为20 ℃。图8为UDDS工况。利用Lossy Counting算法对放电电流进行频繁项统计，将放电电流分割为多个放电区间，每个区间间隔0.2 A，对各区间分别统计积累电量，结果见图9。

图7 电池充放电实验台架

图8 UDDS工况曲线

图9 UDDS工况下电流频繁项分布直方图

如图10所示，在UDDS工况下对传统安时积分法和提出的安时积分法进行了比较。传统安时积分法在进行SOC估计时，累积电量按固定库仑效率乘以电流的积分进行计算。提出的安时积分法，在进行SOC估计时，针对不同放电电流区间，先利用不同库仑效率进行修正，再将修正后的累积电量之和作为放出的总电量计算SOC。

图10 UDDS工况下，2种算法SOC估计结果曲线

实验结果表明：利用传统安时积分法与提出的安时积分法分别进行SOC估计，误差随着实验过程的进行而逐渐增大。在实验进行到2 384 s时，电池到达放电截止电压。此时提出的安时积分法SOC估计结果接近于0。而传统安时积分法由于开环，无法及时修正库仑效率，所估计的SOC值为-8.7%，误差较大。

3.3 实车工况下算法对比

为了验证所提出算法在实车工况下对电池荷电状态的估计效果，对艾恩科技智能车上的电源模块进行了改装，制作了串联的4节NCR18650B电池模组，利用电流传感器、电压传感器、温度传感器、无纸记录仪等设备采集车辆实时工况数据，利用基于频繁项统计的流挖掘算法对电流进行分析。智能小车如图11所示。

图11 智能小车

在利用Lossy Counting算法进行电流区间积累电量统计时，桶的宽度为w，是由系统允许的误差ε决定的。通过调节参数ε，并不需要太多的存储空间和计算资源来统计不同电流区间的积累电量。Lossy Counting算法可自动对积累电量较大的电流区间进行频繁项统计，并忽略积累电量较小的区间。从而最大程度地减少实车上位机端的计算及存储开销。如图12、13所示，并非每一个电流区间都有大量电量积累。

图12 智能小车车速与放电电流曲线

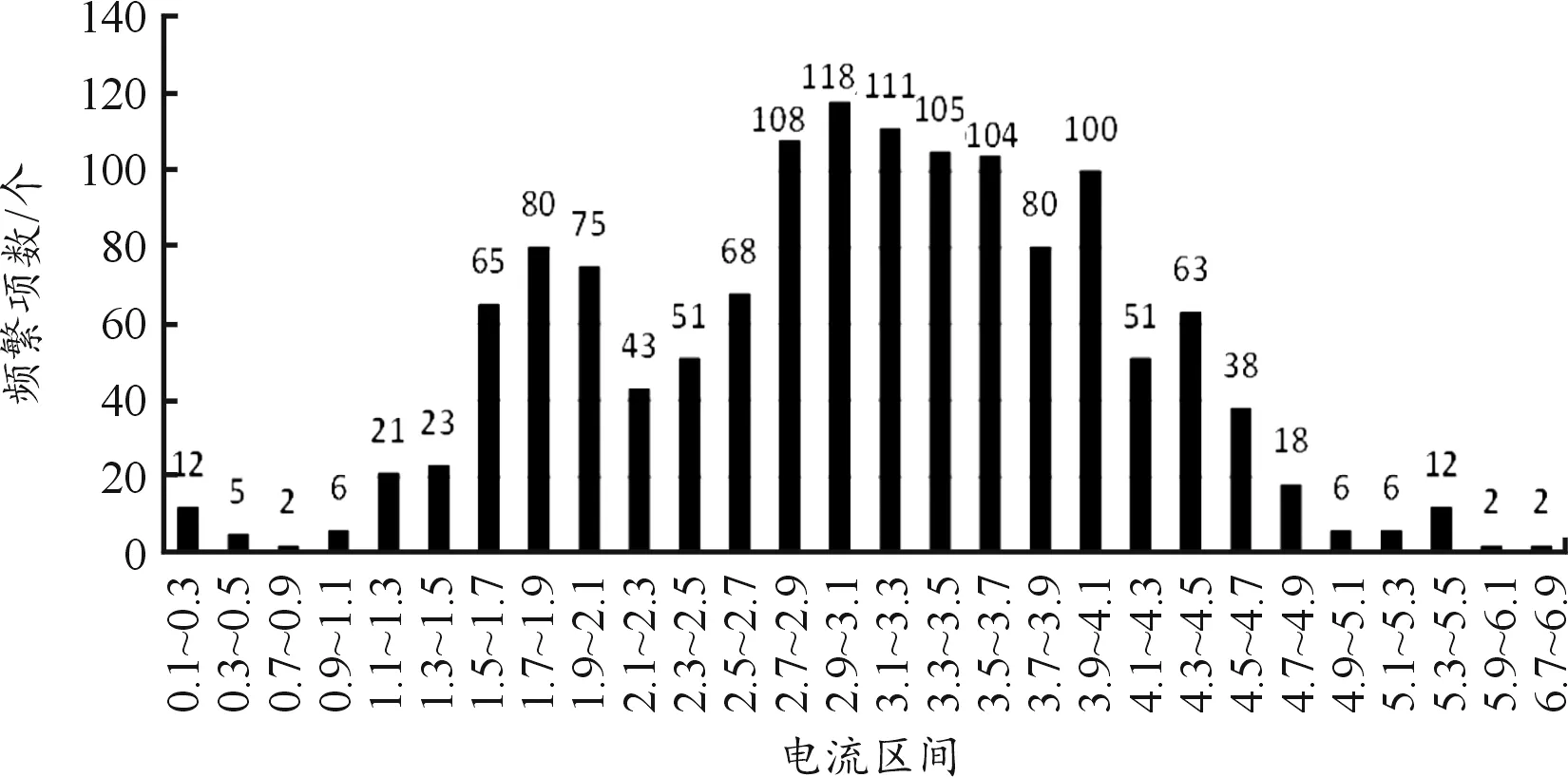
图13 基于频繁项统计智能小车电流分布直方图

利用传统安时积分法与提出的安时积分法进行实车工况下电池SOC估计，结果如图14所示。

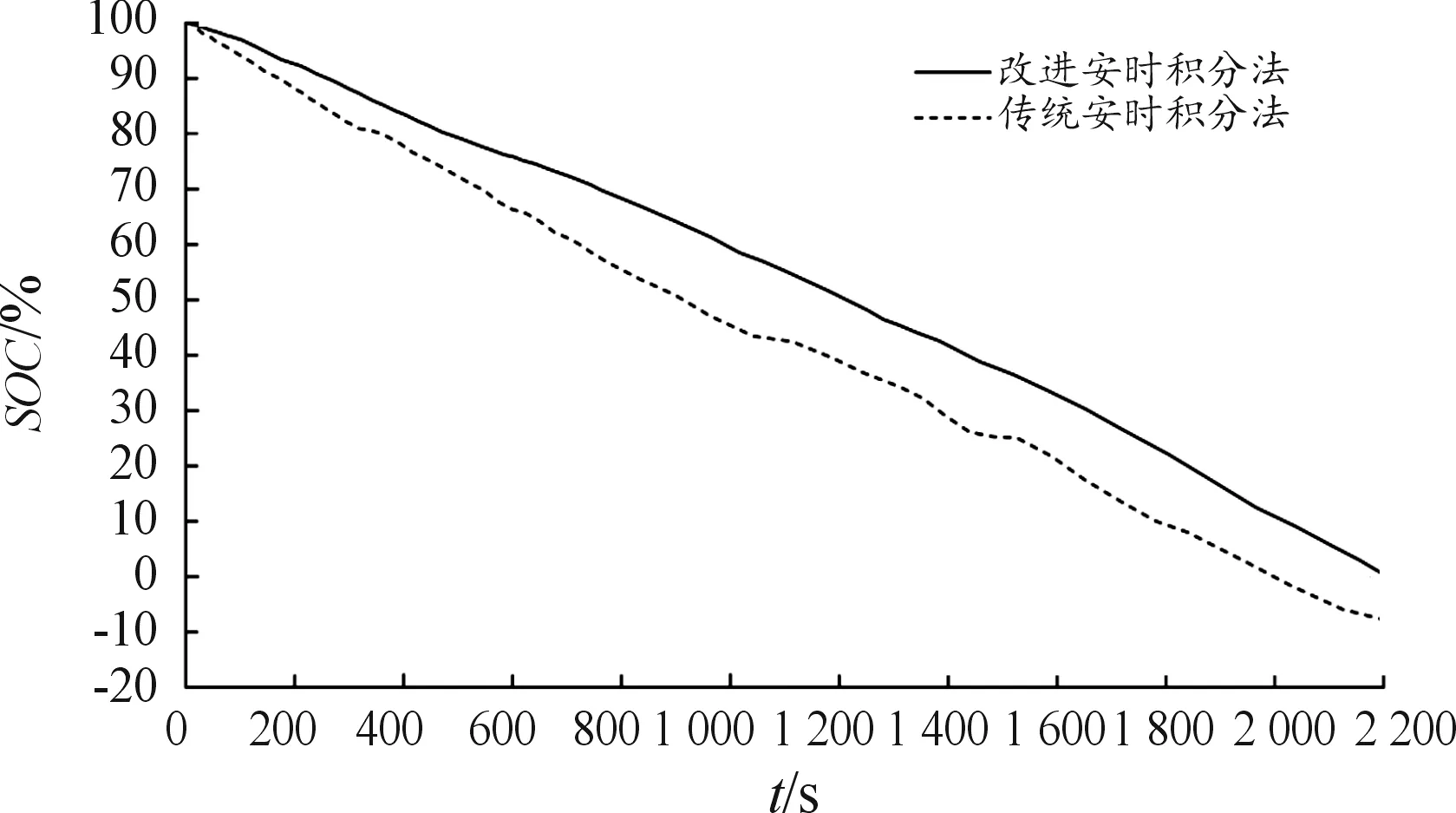
图14 实车工况下，2种算法SOC估计结果曲线

由图14可见，在实验进行到2 200 s时，电池到达放电截止电压。此时提出的安时积分法SOC估计结果接近于0，而传统安时积分法因其累积误差难以修正，其SOC估计为-7.6%，显然误差较大。事实上，提出的基于频繁项统计的安时积分法，不仅可以利用精确的库仑效率对分段积累后的电量进行修正，还可对由于传感器误差、元器件老化引起的测量值漂移进行修正。

3.4 传感器噪声工况下算法对比

为探究传感器噪声对提出算法的影响，在原始电流信号上分别叠加了白噪声和有色噪声。之后，利用提出算法对分段电量进行频繁项统计，结果如图15所示。当白噪声(-0.1～0.1 A)叠加在原始电流信号上时，其频繁项分布(短划红线)与无噪声原始电流信号的频繁项分布(实线)非常相似。当有色噪声(0～0.2 A)叠加在原始电流信号上时，电流频繁项分布(圆点蓝线)相对无噪声原始信号向右侧移动。

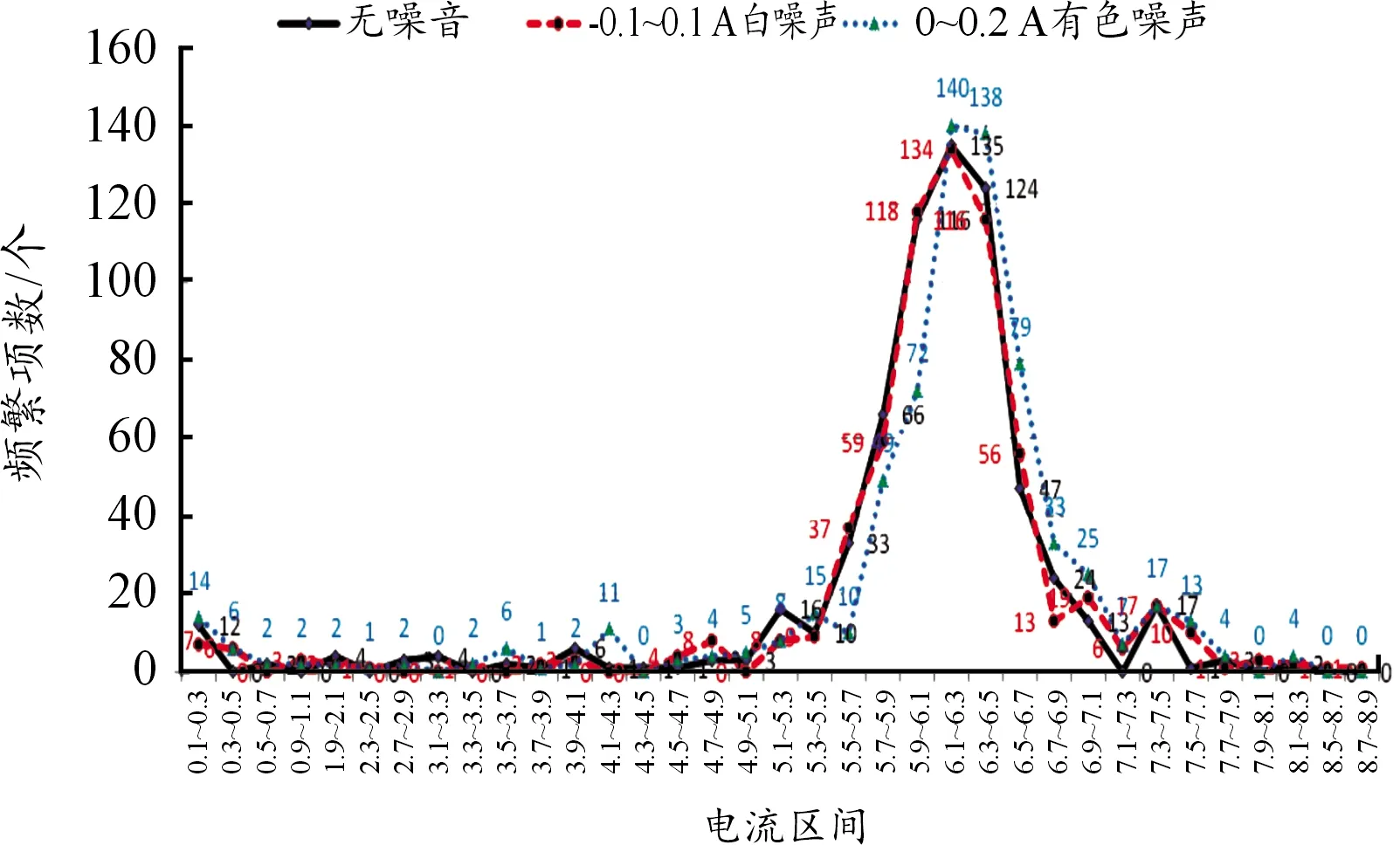
图15 传感器噪声对提出算法中积累电量的影响曲线

图16和图17分别显示了多次充放电循环过程中，不同噪声对2种安时积分法SOC估计结果的影响。通过对比不难发现，当白噪声(-0.1～0.1 A)叠加在原始电流信号上时，2种安时积分法估计的误差变化不大。当有色噪声(0～0.2 A)叠加在原始电流信号上时，用传统库仑计数方法获得的相对误差增加，但用提出的库仑计数方法获得的相对误差在运行了十几次充放电循环后，逐渐减小。这主要是由于充放电次数增多，所提出的安时积分法获得了足够多的积累电量，可基于式(8)构建库仑效率方程组，对库仑效率矩阵进行在线更新，从而解出了病态的库仑效率来抵消有色噪声对SOC估计结果的干扰，从而提高估算精度。

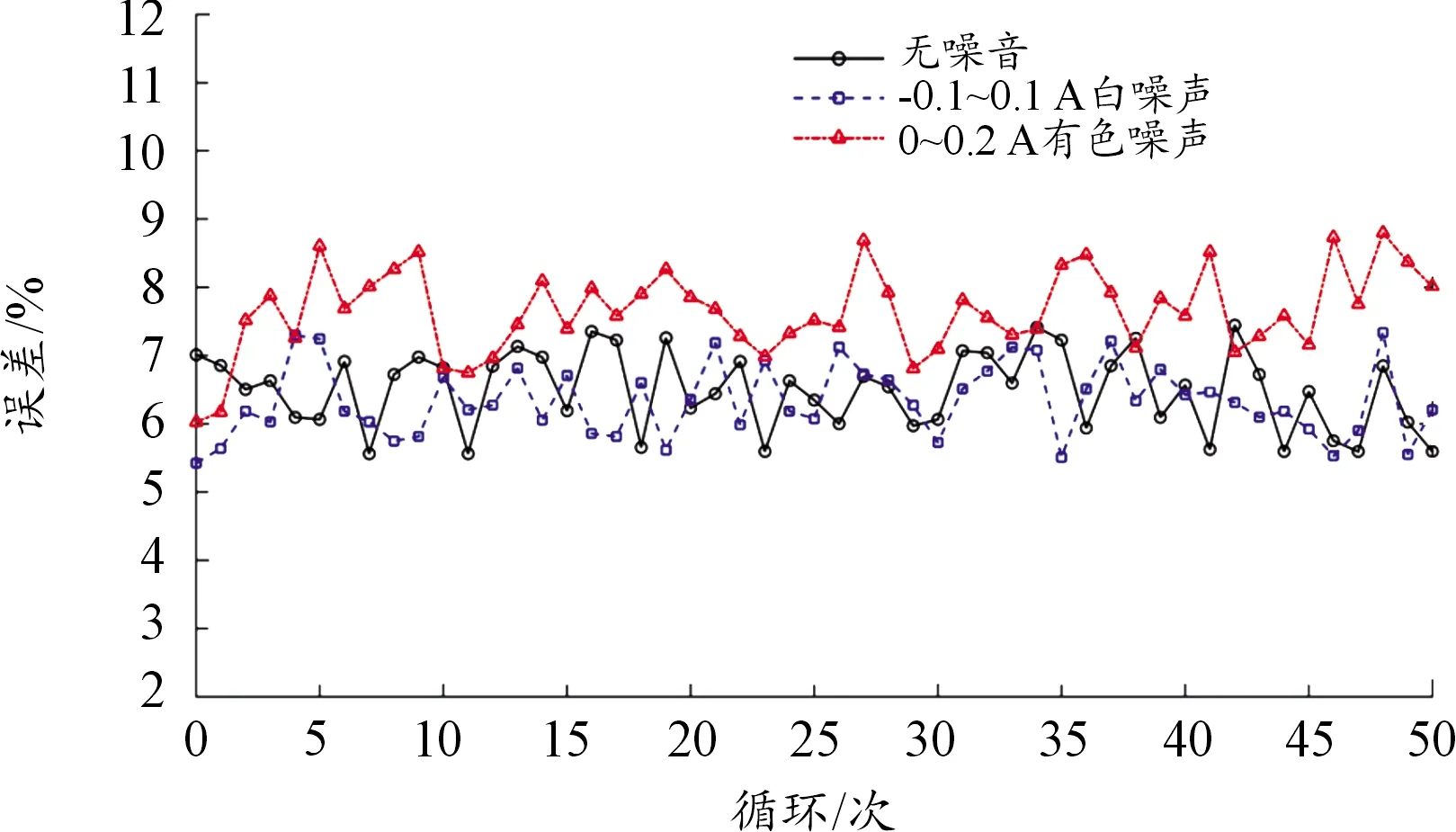
图16 噪声对传统安时积分法的影响曲线

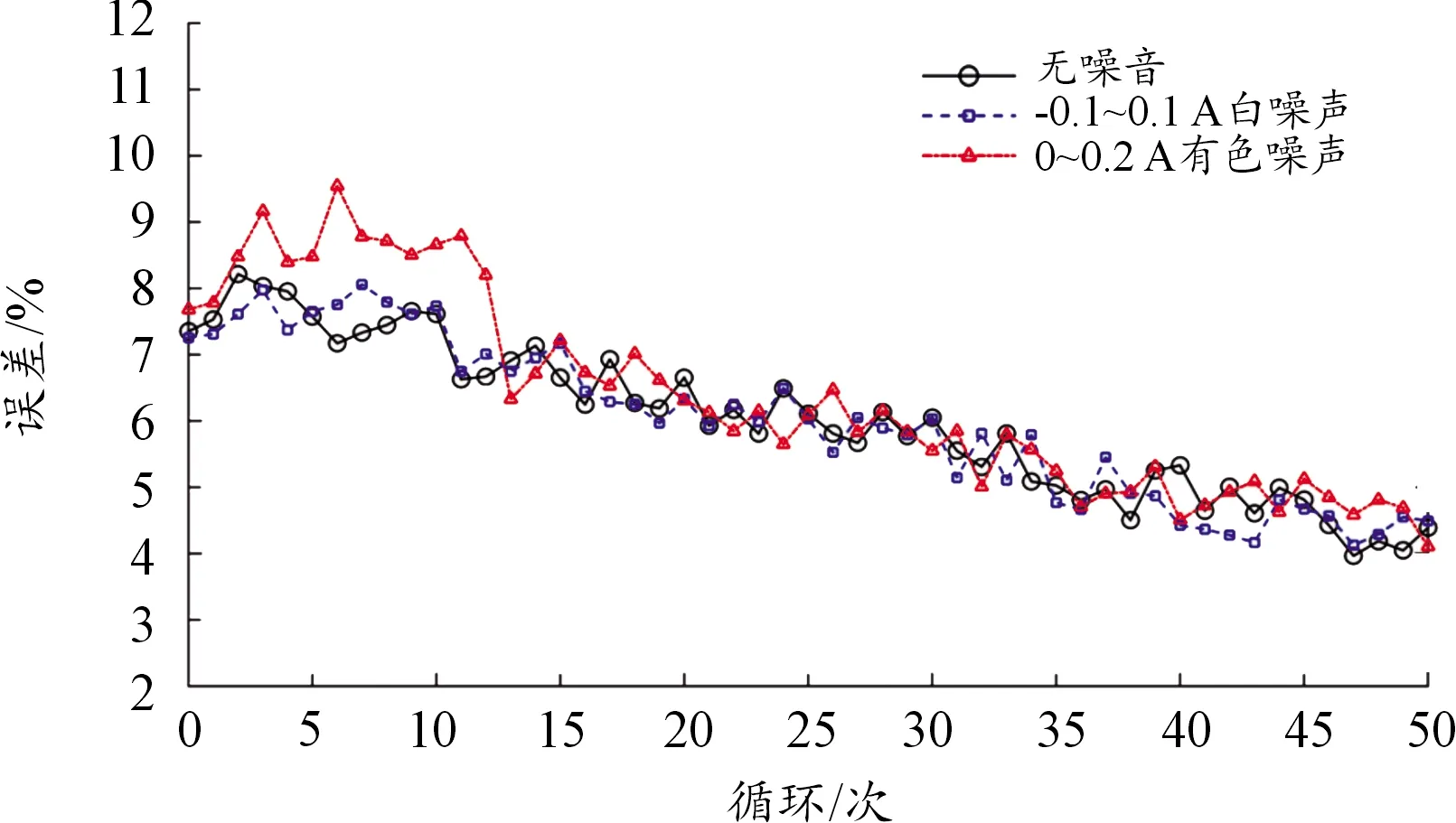
图17 噪声对提出的安时积分法的影响曲线

4 结论

与传统的安时积分法相比，本文提出的基于频繁项统计的流-安时积分法，构造了概要数据结构，在线修正了库仑效率矩阵，降低了剩余容量、工作电流、温度、SOH等环境因素对算法的影响，抵消了传感器误差及元器件老化所导致的测量参数值的概念漂移，以较小的存储空间、较少的计算资源，提高了传统安时积分法的估算精度。