动态环境下AGV避障轨迹规划问题研究
何均锋,李 鹏,申艳红,邹安帮,熊 威,吴婷婷
(南京林业大学 汽车与交通工程学院, 南京 210037)
自动导引车(automated guided vehicle,AGV)是指在导航信息的导引下在地面上移动的移动机器人[1]。合理的AGV路径规划不但能提高仓库的货物周转率和订单完成效率,也能使AGV的行驶更平稳[2]。运动规划是AGV完成作业任务运动控制的基础,直接决定了AGV的工作质量[3]。
目前,路径规划算法主要分为基于图搜索的路径规划、数值优化、基于样本的路径规划、插值算法这4类[4-5]。考虑到实际应用的简单性,图搜索方法比传统的路径规划策略更有效[6]。例如,Dijkstra和A*算法等经典的图搜索算法都被广泛用于搜索最短路径[7-8]。吴鹏等[9]在传统A*算法的基础上增加了正反向搜索的机制,然而其使用范围只是局限于静态障碍物环境下。Xu等[10]以时间最优为代价函数,用带有优先约束(TSPP-PC)旅行商问题来表示AGV的路径规划问题,并基于精确算法提出了一种启发式算法来进行求解。Lim等[11]和Zhang等[12]在Shih等[13]通过图搜索器在时空域中规划一个粗略的轨迹的基础上进行了参数优化计算,但未考虑与AGV运动学相关的非完整约束,并且障碍物的轨迹被限定,存在局限性。Corman等[14-15]提出将事件动态和连续时间动态模型离散,把AGV与码头QC和ASC的作业过程视为混合流水车间调度,以时间最短为代价函数,采用启发式算法以一种近似最优的方法来求解,但该过程只考虑静止障碍物,并未将动态障碍物纳入考虑范围。Xin等[16]在离散事件动态和连续时间动态的基础上提出了滚动时域状态监测控制器,以能耗最优为代价函数,采用事件驱动能效算法求解模型,但未对AGV的碰撞约束进行考虑。赵鑫等[17]基于A*算法改进得到ARA*算法,首先将约束条件松弛,搜索出一条次优路径,然后在加强约束条件的情况下改进次优解。
本文将移动障碍物轨迹随机环境下的AGV轨迹规划问题归结为一个最优控制问题。利用直接配点法将最优控制问题离散成一个非线性规划问题,然后用常见的内点法进行寻优。同时,为了快速求解非线性规划问题,对传统的A*算法做了改进,生成一条初始轨迹作为优化过程的初始解。仿真表明,改进A*算法能有效搜索出一条无碰的初始轨迹,利用直接配点法优化后的轨迹在满足约束的前提下与初始轨迹基本一致。
1 避障描述
一般AGV轨迹规划问题可以转化为一个最优控制问题,即在满足运动学约束、避碰约束和边界条件的情况下,使得代价函数最小化。
1.1 AGV运动学
两轮差速AGV运动平面图如图1所示,X-Y坐标系为全局坐标系,XR-YR坐标系为AGV车身坐标系,M处于驱动轴的中间位置,C为小车的质心所在,设方向以逆时针为正,AGV运动学描述为:

(1)

图1 AGV运动平面图
具体的参数含义见表1:

表1 参数与定义说明
在[0,tf]时间内AGV移动过程中,存在几个边界限制其移动,运动约束如下:
(2)
其中,vmax、amax和ωmax分别代表相应变量的最大值。
1.2 避碰约束
用包络圆柱来覆盖障碍物,其在AGV运动平面上的投影是圆形。假设在[0,tf]内每个障碍物的位置都可以被正确地预测,则第i个障碍物的圆心(xobs_i(t),yobs_i(t))和半径Robs_i(t)在t∈[0,tf]内任何时刻的位置已知。
在实际工作中,AGV的车身外形是矩形,但涉及矩形的避碰约束非常复杂,因此采用外接圆来覆盖AGV的矩形车身,其避碰约束如式(3)所示:
(3)
1.3 边界约束
假设AGV在t=0和t=tf的2个时刻分别处于起始位置和终端位置,则起始时刻约束设置如式(4)所示:
(4)
式中:x(0),y(0),θ(0),v(0),a(0)和ω(0)是初始时刻参数。
由于实际情况下的AGV并不一定能够按期望到达理想位置,因此需要对终点约束进行松弛,部分参数[v(tf),a(tf),ω(tf)]设置如式(5)所示:
[v(tf),a(tf),ω(tf)]=[vf,af,ωf]
(5)
式中:v(tf),a(tf),ω(tf)是终止时刻参数。
1.4 代价函数
在实际情况下,由于AGV的定位误差等原因,AGV并不一定能严格地到达期望的目标位置,为了使AGV在终止时刻的位置[x(tf),y(tf),θ(tf)]尽可能地靠近期望的终端位置[xf,yf,θf],则以x(tf)、y(tf)、θ(tf)分别与xf、yf、θf的差的平方和作为代价函数,即代价函数为:
(6)
1.5 最优控制问题建立
综合上述约束条件以及代价函数,AGV的避障轨迹优化问题可以归结为以J为代价函数,以车体质心加速度α和车体质心角速度ω为输入,满足运动约束、避碰约束、边界约束的最优控制问题,如式(7)所示:
(7)
2 轨迹规划
2.1 基于改进A*算法的轨迹规划
为获取一个初始轨迹作为非线性规划问题的可行初始解,运用一种改进A*算法来生成运动轨迹。与传统的A*算法相比,改进A*算法在AGV二维运动平面的基础上加入了时间维作为第三维度,形成轨迹空间。
改进A*算法建立了轨迹空间,然后将连续x-y-t状态空间用有限网格表示,定义抽象空间中的每个网格为节点,指定起始节点A和目标节点B,并标记移动障碍物占据的节点。
与传统A*算法一样,改进A*算法也有2个函数,即g(s)和f(s)。g(s)衡量从起始节点A到s的路径成本,而f(s)=g(s)+h(s)用来估计经由s从起始节点A到目标节点B的总成本,选取欧氏距离作为h(s)的代价函数,函数表示为:
(8)
式中:(xs,ys)代表当前状态节点的坐标,(xB,yB)代表目标点节点坐标。
改进A*算法和传统A*算法一样,都有一个OPEN表,将起始节点A加入OPEN表中,并且将要展开的节点以f(s)的递增序列记录。一旦有效节点s被扩展,则将其从OPEN表中移除,并且将其所有未被扩展的有效子节点添加到OPEN表中,同时把这些有效子节点的父节点设为s,路径成本则为:
f(s′)=g(s)+c(s,s′)+h(s′)
(9)
式中:c(s,s′)为计算相邻两级节点s和s′之间的代价。如果s′已经在OPEN表中,则表明s′已经预先得到f(s)的值,这种情况下令
f*(s′)=g(s)+c(s,s′)+h(s′)
(10)
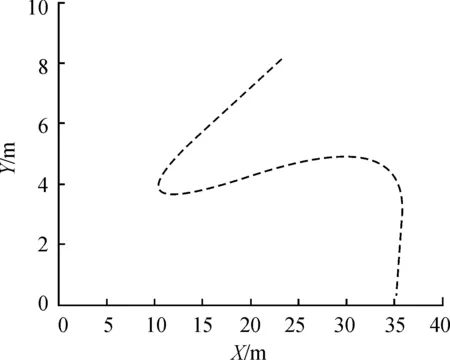
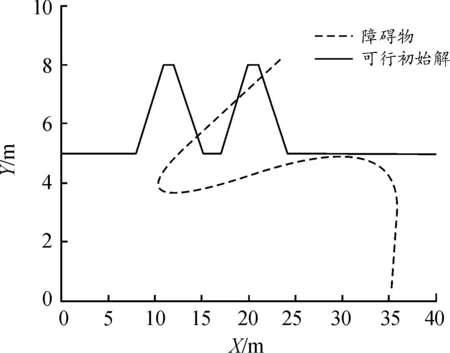
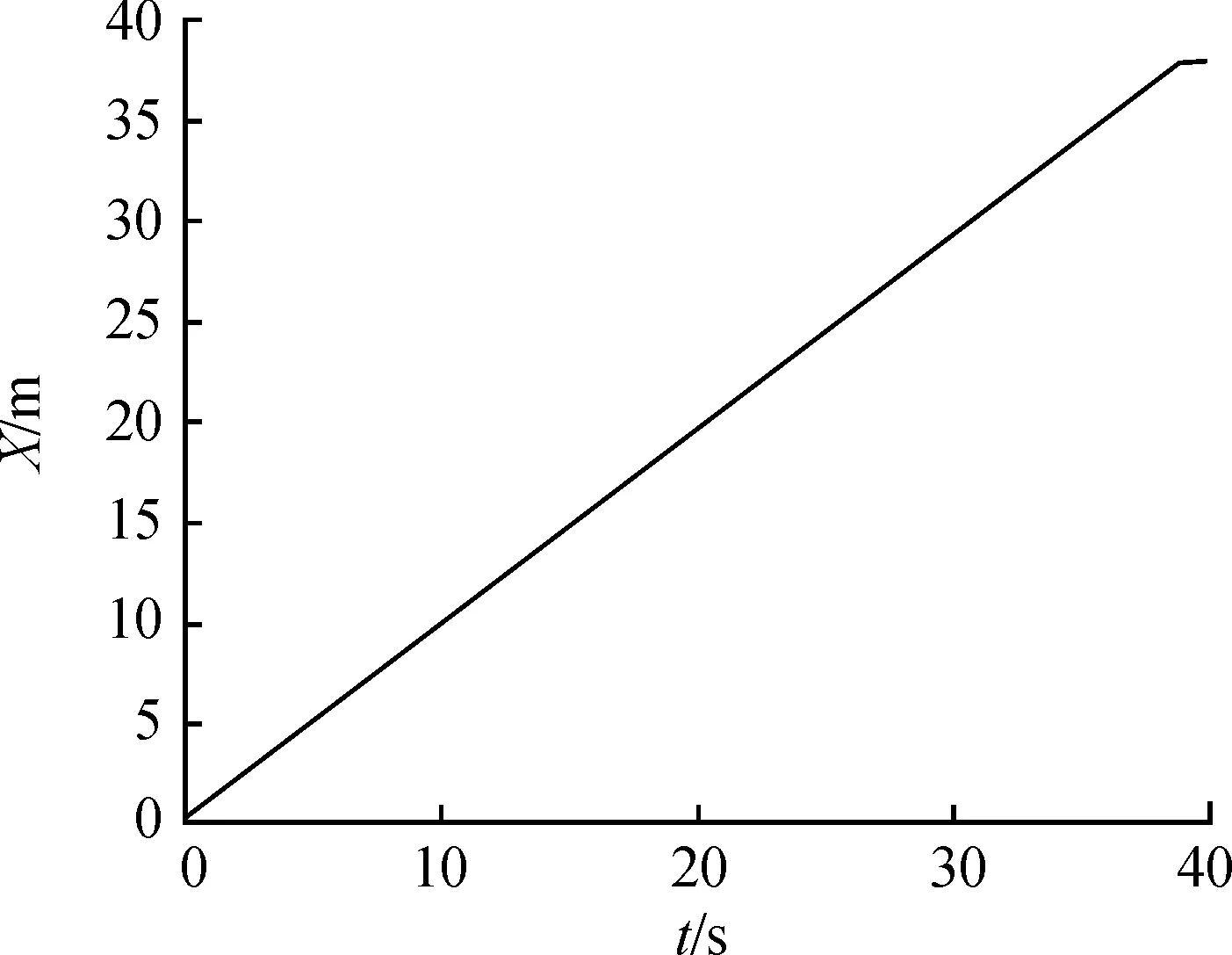
如果f*(s′) 图2 改进A*算法流程框图 由改进A*算法搜索出的轨迹存在尖点,无法满足AGV的运动学约束,因此需要进行轨迹优化。针对轨迹优化问题,采用数值方法求解前文所提出的最优控制问题,采用直接配点法将最优控制问题离散成一个多约束的非线性规划(nonlinear programming,NLP)问题。 直接配点法(direct collocation method,DCM)最早由Hargraves等[18]提出,可以同时离散控制量和状态变量。首先,整个时间过程将被分割成N个小段,分割后的每一小段端点称为“节点”。对于节点之间状态变量随时间的变化关系,通常采用高斯-洛巴托多项式族来表示,由于在区间 [-1,1]上,Jacobian多项式是正交多项式族,因此配点依据具体的Jacobian多项式来选取。非线性规划问题的优化设计变量主要包括节点处的状态变量、节点和配点处的控制变量。最后,在满足各类约束的条件下对代价函数进行寻优。 针对轨迹优化问题,选用三阶Simpson公式来拟合节点间状态变量,具体描述如下: 1) 离散时间历程,即: t0=t1 (11) 用(X1,X2,X3,…,XN)表示时间点对应的状态变量,(U1,U2,U3,…,UN)表示时间点对应的控制变量。 2) 参数化状态变量与控制量。 用三次插值多项式来近似表示子区间上的状态变量,即: (12) 子区间[ti,ti+1]的边界条件如式(13)(14)所示: X(0)=Xi,X(1)=Xi+1 (13) (14) 则: (15) 式(15)中的多项式系数、区间端点状态变量和其导数的代数方程组可以依据式(14)中的边界条件建立,求解式(15)可得: (16) 取子区间中点处(h=0.5)作为配点,将式(16)代入式(12),可得: (17) 采用分段线性函数来近似控制变量,设uj为某个区间控制变量的第j个值,则: (18) 3) 计算配点的defect向量(该向量构成了系统的非线性等式约束)。 为确保三次多项式能更好地拟合状态变量的变化,应使式(19)中defect向量的期望值无限逼近于零。 (19) 式中:M为子区间配点处的状态方程计算的状态变量导数,XM为多项式求得的状态变量导数。 4) 求解非线性规划问题。 求解代价函数J最优解的非线性规划问题需要满足以下2个方面要求:① 满足配点处约束,即defect=0;② 满足原最优控制问题的约束条件。设计变量y如式(20)所示。 (20) 轨迹优化问题可转化为式(21)中带约束的非线性规划问题,即: (21) 式中:Q为代价函数;pk(y)为非线性规划问题的不等式约束;qk(y)为等式约束。 综上所述,最优控制问题可以以式(21)的形式来表述,其中Q表示代价函数J;pk(y)表示运动约束、避碰约束;qk(y)表示两点边界约束;y表示x(t),y(t),θ(t),v(t),a(t),ω(t)等变量。 离散后得到(2N+1)×4个状态变量的离散值和(2N+1)×2个控制变量的离散值。离散化后的状态变量和控制变量为: (22) 将控制变量的约束条件施加于节点及配点的控制变量离散值处,则可得: (23) 碰撞临界约束转化为节点处的状态变量离散值的约束: (xAGVk-xobs_ik)2+(yAGVk-yobs_ik)2≥(RAGV+Robs_i)2 k=0,1,2,…,N-1,N (24) 将代价函数转化为末端配置点处与期望位置的距离,即: minJ=(xN-xf)2+(yN-yf)2+(θN-θf)2 (25) 最后,采用在求解非线性规划问题过程中常见的内点法来优化求解。 基于直接配点法的优化求解原理如图3所示。 图3 基于直接配点法的优化求解原理示意图 为了验证所提出的轨迹规划的有效性,在Matlab平台上建立仿真算例,基本参数设置如表2所示。 表2 AGV参数 在仓储环境中,存在的移动障碍物一般为除自身以外的其他AGV,设置所有AGV在40 m×10 m的区域上运行,运行时间tf设为40.0 s,AGV的起始位置与目标位置分别设为(0,5)和(40,5)。在[0,tf]期间,每个移动障碍AGV的轨迹被设置为具有4个随机节点的B样条曲线,AGV的车身外接圆半径设置为0.5 m。初始参数[x(0),y(0),θ(0),v(0),a(0),ω(0)]设置为[0,5,0,0,0,0]。 图4为单障碍运动轨迹在XY平面内的投影,图5为多障碍运动轨迹在XY平面内的投影,分别在单个和多个移动障碍物环境下,利用改进A*算法搜索生成的可行初始解,在障碍物轨迹投影平面内的投影分别如图6、7所示。 图4 单障碍运动轨迹在XY平面内的投影曲线 图5 多障碍运动轨迹在XY平面内的投影曲线 图6 单障碍物轨迹投影平面内的可行初始解投影曲线 图7 多障碍物轨迹投影平面内的可行初始解投影曲线 图8为AGV在单障碍物环境下与障碍物圆心距离的变化曲线,图9为AGV在多障碍物环境下与障碍物圆心距离的变化曲线。图8中AGV与障碍物圆心的最小距离为3.19 m,图9中AGV与障碍物圆心的最小距离为2.782 m,大于预设的安全距离1.2 m,表明改进A*算法生成的初始轨迹是可行的,验证了改进A*算法在动态障碍物环境下可以有效地搜索出一条无碰轨迹。 图8 AGV在单障碍物环境下与障碍物圆心距离的变化曲线 图9 AGV在多障碍物环境下与障碍物圆心距离的变化曲线 图10、11分别为单个障碍物环境下优化解的X、Y坐标的变化曲线,图12、13分别为多个障碍物环境下优化解的X、Y坐标的变化曲线。如图14、15所示,在单障碍物环境或者多障碍物环境下,优化前后的轨迹大致上相同,但优化后的轨迹更加平滑。 图10 单障碍物环境下优化解的X坐标变化曲线 图11 单障碍物环境下优化解的Y坐标变化曲线 由图14、15可知,代价函数在每一时刻的梯度都是下降的且在结束时刻趋于平缓,因此优化后的轨迹能在避开障碍物的同时向目标点逼近。 图12 多障碍物环境下优化解的X坐标变化曲线 图13 多障碍物环境下优化解的Y坐标变化曲线 图14 代价函数在多障碍物环境下的变化曲线 图15 代价函数在单障碍物环境下的变化曲线 将AGV在复杂动态障碍物环境下轨迹规划问题转化为最优控制问题,将改进A*算法与直接配点法相结合进行轨迹规划。基于改进A*算法进行搜索生成初始轨迹,结果表明,在单障碍物和多障碍物环境下,AGV外接圆和障碍物外接圆的最小圆心距分别为3.19 m和2.78 m,满足本文预设的安全距离要求,因此利用改进A*算法能有效搜索出一条无碰的初始轨迹。然而,初始轨迹存在尖点,无法满足AGV的运动学约束,因此,本文采用了直接配点法进行优化。先对最优控制问题中的变量进行离散,将最优控制问题转化为带约束的非线性规划问题,再利用非线性规划问题求解中常见的内点法寻优。优化结果表明,优化后的轨迹在满足运动学约束的情况下与初始轨迹基本一致。另外,代价函数在每一时刻的梯度都是下降的且在结束时刻趋于平缓,因此优化后的轨迹能在避开障碍物的同时向目标点逼近。本文轨迹规划方法具有很强的应用性,可适用于障碍物随机移动的情况,对将来AGV在动态障碍物环境下的避障轨迹规划研究有借鉴作用。
2.2 基于直接配点法的轨迹优化
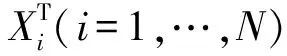

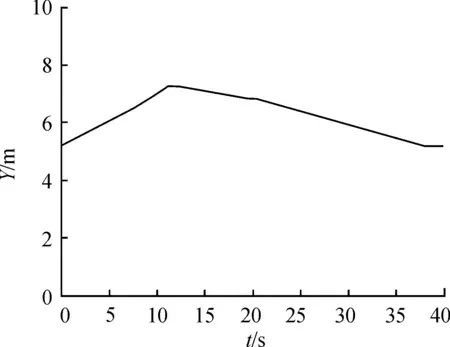
3 仿真结果









4 结论

