某列车用动力电池系统风冷散热流场研究

赖晨光，余 琴，宋 洁，陈 祎，孙友长，谭 伟

(1.汽车零部件先进制造技术教育部重点实验室(重庆理工大学), 重庆 400054；2.重庆理工大学 车辆工程学院， 重庆 400054；3.中国汽车工程研究院股份有限公司， 重庆 401122)

由于世界能源危机的爆发，石油价格迅速上涨，为了减少我国对石油的依赖，同时减轻燃油对环境的污染，新的车用动力元件应运而生，锂离子动力电池就是其中一种，现有的锂离子电池主要包括磷酸铁锂电池、锰酸锂电池、三元锂电池等。作为储能、动力元件，动力电池系统是否可靠，直接影响着车辆的性能，而动力电池的性能和寿命受温度的影响十分显著，电池温度一般维持在20～50 ℃[1]，如果散热不充分，温度过高，将会使其可靠性降低、使用寿命缩短[2],因此，合理的散热必不可少[3]。在电池投入生产之前，对电池在各个工况下进行数值模拟分析，预测其散热性能以保证其温差被控制在合适的范围内，具有现实意义。

动力电池系统列车发展前景广阔[4]，国内外都有了较多的研究，自2013年首辆电池电动机车研制成功以来[5]，电池在列车上的应用发展得越来越快。在现有的列车动力系统中，动力电池主要包括燃料电池和锂离子电池，但由于锂离子电池比能高、电压高、放电倍率高、循环寿命长、无污染[6]等优异的性能，应用较为广泛，且被认为是未来动力电源产业的领军者。磷酸铁锂电池除了具有锂离子电池基本的优点外，还由于其温度范围广、原材料来源丰富等特点，被动力电池企业广泛采用。郑鑫等[7]通过对磷酸铁锂电池散热过程的仿真分析，预测出了电池温度的发展趋势，为电池系统中电池箱的设计提供了参考。温差对电池系统有着重要的影响，Watkins等[8-9]发现合理的电池热管理系统能很好地调和电池间的温差，在很大程度上提升电池组的性能。为了保证电池间温度的均匀性，动力电池系统需要散热，其分类方式以冷却介质作为依据，主要分为空气冷却、相变材料冷却和液冷3大类，许多专家在这些方面做了研究[10-13]。除此之外，还有热管散热[14]。由于风冷散热系统结构较为简单，制造成本低，电池组的整体质量较小，不可能发生漏液，因此，该冷却方式被当成车辆电池系统散热的首选[15]。而自然风冷受车速、环境温度等外在因素的影响，效果极不稳定，因此发展出了强制风冷的电池组散热系统[16-17]。Choi[5]、赵德华、彭影等[18-19]就做了有关风冷强制对流换热方面的研究，通过实验与仿真，发现强制风冷能有效地使电池系统工作在合理的温度范围内。

本次研究以某列车用空调强制风冷磷酸铁锂动力电池系统作为研究对象来探究空调对电池的散热效果，主要针对电池组散热流场，而数值模拟方法能方便地提供全部流场范围的详细信息，因此利用STAR-CCM+对电池系统进行仿真，得到在充电和放电过程中温度的变化规律，将仿真结果与实验结果进行对比，有效地对电池的散热特性进行分析。

1 数值计算模型

锂离子电池产生的热量来源于电池工作时，电池内部进行的各种电化学反应以及锂离子、电子脱嵌或迁移等产生的热行为，总热量主要由焦耳热、反应热、极化热与副反应热4部分组成，其热量传递方式分为热对流、热传导和热辐射3种[20]。锂离子电池在工作时，电池的温度相对较低，热辐射向外部传递的热量很小，且本文的散热方式为风冷，也不考虑电池内部的传热，因此主要针对热对流情况对电池散热进行分析，热传导和热辐射因素暂不考虑。锂离子单体电池的热量主要有2个流向：一部分热量与外部介质进行热量交换，在交换过程中带走电池产生的热量，从而使电池温度降低，达到散热的目的；另一部分热量则由电池自身吸收，也正是该部分热量将最终导致电池温度升高。

1.1 电池生热模型

截至目前，国内外对锂离子电池进行了大量的研究[21-26]，但受到电池工作时外界环境因素的影响，尚未开发出一个通用的、非常精准的生热速率理论计算模型。在现有的锂离子电池热模型中，BERNARDI[27]的方程被广泛用于电池生热速率的计算，其假设电池是一个均匀且稳定的生热源，不考虑电极反应中活性物质的浓度、电流密度等参数的空间差异,该模型的数学表达式为

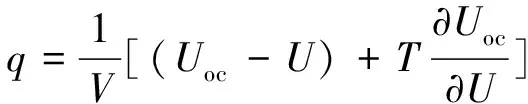
(1)

1.2 流动及传热控制方程

磷酸铁锂电池组温度过高时，通过空调强制换热，这个过程主要涉及了流动与热交换，且二者均遵循质量守恒定律、能量守恒定律以及动量守恒定律[28]。质量守恒方程：

(2)

式中：ρ为密度，kg·m-3；t为时间，s；u、v、w为x、y、z方向的速度分量。

动量守恒方程：

(3)

式中：Su为动量方程的广义源项，该式为x方向的守恒方程，y、z方向同理。

能量守恒方程：

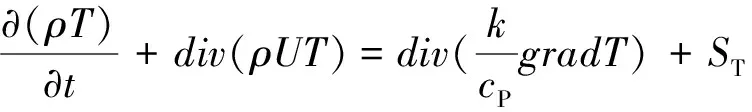
(4)

式中：cP为比热容，J·kg-1·K-1；T为电池温度，℃；k为传热系数，W·m-2·K-1；ST为流体的黏性耗散项。

对于方程的求解，根据其理论推导以及离散方法的差异，目前主流的方法包括有限体积法(finite volume method)、有限元法(finite element method)、有限差分法(finite difference method)[29]。其中，有限体积法又叫控制体积法，这种方法发展虽然比较晚，但是计算效率很高，原理较为简单，应用最为广泛，也是本次研究的求解方法。

2 模型仿真与实验

2.1 模型及边界条件

图1为1/2电池箱，本次研究所用的风冷磷酸铁锂动力电池组为对称构型，其由电池数量和排列方式相同的4个板块组成，各个板块的结构一致，故只做1/4模组的模拟。该1/4模组电池包由上至下分别命名为Model一步1、Model 2、Model 3、Model 4、Model 5，从右到左分别命名为Cell 1、Cell 2、Cell 3，如图2、图3所示，Cell 1电池单体的数量为1 620节，Cell 2为1 800节，Cell 3为1 740节。其中，在每个电池模组中，电池箱中的2个边角被隔板隔离，空调入风口和出风口均在电池箱上表面，气流从入风口进入，流到电池箱底部后再回到顶部，从出风口流出，往复循环。网格划分采用切割体网格，整个模型最小网格尺寸设置为1 mm，最大网格尺寸为12 mm，最终体网格总数量为 4 443万左右，其中电池箱内流体体网格数量为2 600万，电池内部体网格数量为1 843万，部分体网格如图4所示。

流动边界条件设置：入风口速度入口，单位时间内速度约为10.6 m/s，出风口压力出口，基准值为0 Pa。

热边界条件设置：湍流模型为K-Epsilon模型，时间离散为隐式不定常。电池质量为0.085 kg，密度为2 500 kg/m3，比热容及导热系数等参数由计算得出，其属性不随时间和温度的变化而变化，电池为电池箱内主要的发热源，空调制冷效果边界由1 kg的空气根据空调12 kW的制冷功率计算得出。

图1 1/2电池箱示意图

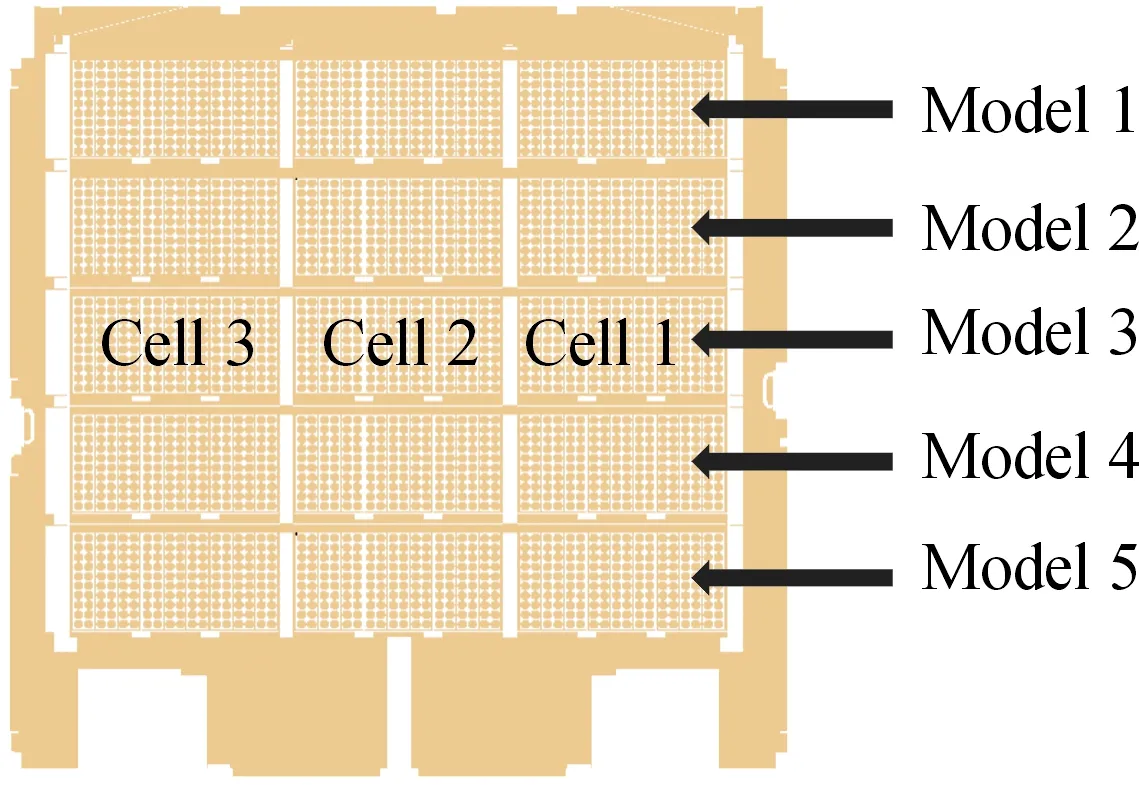
图2 电池包中截面

图3 电池几何结构俯视图

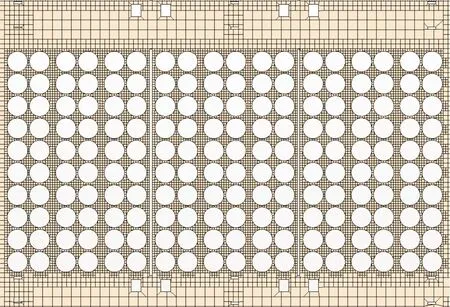
图4 电池包中截面部分体网格示意图

2.2 计算结果分析

考虑到电池工作时的散热复杂性，以表1中2个工况为例，探究在空调制冷的作用下强制换热时电池系统工作的温度场、速度场、压力场以及相关参数随时间的变化情况。在这2个工况中，持续3 042 s放电后再持续3 042 s充电为一个工作循环(0～6 084 s)，工况1在循环结束后再间歇5 min。工况2空调的工作状态以监测点的最高温度与最低温度之和的平均值为约束条件来进行确定，当监测点的最高温度与最低温度之和的平均值低于35 ℃，则空调的工作状态为无制冷但通风；高于35 ℃，但低于40 ℃，则空调的工作状态为半制冷且通风；高于40 ℃，则空调的工作状态为全制冷且通风。

表1 模拟工况

工况1(0～6 084 s)充放电过程中，风机将空调产生的冷却气流从电池箱顶部泵入箱体内部，气流自上而下经过Model 1-5，最终从出风口流出并进入下一个制冷循环过程。在此循环过程中，模组中的电池单体与冷却气流进行对流换热，达到降低温度的目的；同时，电池模组周围的热空气被循环流动的冷却气流带到电池箱出风口，热量最终由空调换热器带出电池箱。充放电结束后，得到电池模组的计算结果，以放电结果(3 042 s)为例进行电池工作状态分析，图5-8所示为其温度场、速度场以及压力场。

图5 X方向中截面温度云图

由温度云图(图5)可知，电池组整体温度由Model 1至Model 5逐渐升高。冷却气流被泵入箱体内部后直接与Model 1的上表面接触，此时气流流速较高且温度较低，与Model 1上表面的温差较大，因此冷却气流能很快与Model 1上表面进行换热并将热量带走，使Model 1上表面的温度最低。然而，冷却气流自上而下与电池表面不断换热的同时也将电池组上部所产生的热量带到了下部，使冷却气流的温度从上至下逐渐升高，此时气流与Model 5的温差小于气流流过上面Model 4电池时的温差，由牛顿冷却定律可知，单位时间从单位面积散失的热量与周围媒质和物体表面的温度差成正比，因此Model 5电池的换热效率相对较低，热量不能及时被冷却气流带走，导致热量在Model 5处形成堆积。且此时由于箱体下部的阻碍作用，热气流仍不能及时流出，最高温度出现在Model 5下部。由前文可知，Cell 3总体比Cell 1多了120节单体电池，虽然电池间有一定的间隙让气流通过，但该电池间隙相对于电池的尺寸来说很小，与气流直接流向开阔区相比，气流在Cell 3中的流动会受到很大的阻碍，气流的流动阻力增加，使得在相同的时间内Cell 3流过的冷却气流大幅度减少，降低了换热效率。此外，电池数量的增加使Cell 3的生热功率相对较大，生热功率增大就意味着产生更多热量。因此，在热功率增加和阻滞作用增强的共同作用下，Cell 3下部也形成热量堆积，导致整体温度高于Cell 1。

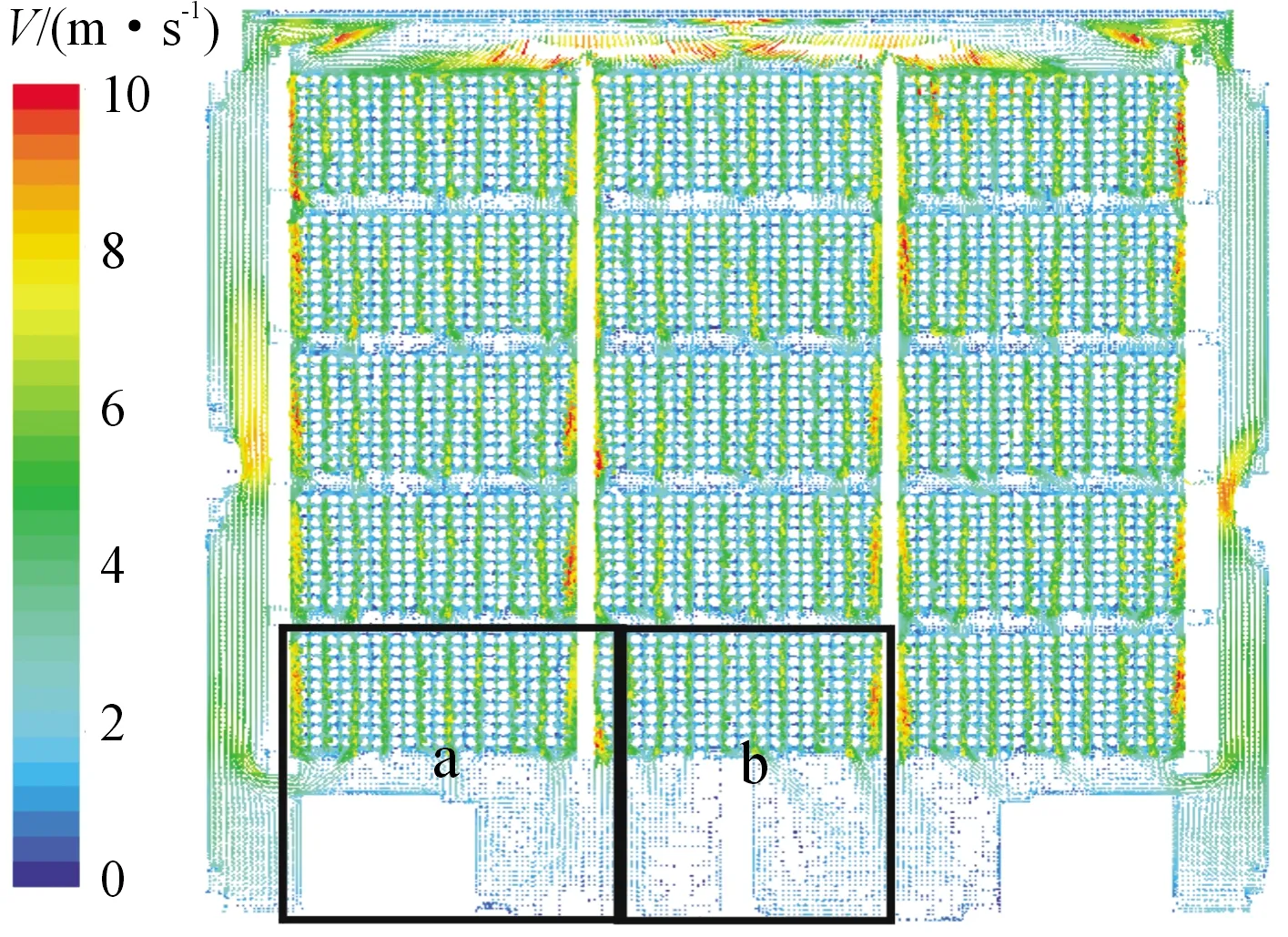
图6 X方向中截面0～10 m/s速度矢量云图

由图6可见，气流沿电池组边缘流动的速度比电池单体间的流动速度大，而气流流速快，增大了电池表面的湍流流动，有利于带走电池更多的热量，使气流流速较快，区域的电池温度更低。而电池组内部电池单体间隙小，冷却气流流动困难，对流换热效率低，散热效果较差，所以电池箱内模组间整体温度呈金字塔状，靠近电池箱边缘的单体电池温度较低。气流流过Model 5的Cell 3(图7 a区域)以后，Cell 3左边部分气流向左流动，进入回风道，右边部分气流向电池箱底部开阔区域流动，流动阻力较小，有利于带走该模组右侧区域的热气流。但在Cell 3的中间部分，由于底部有矩形箱体对下行气流的阻碍，该区域气流出现部分回流现象，回流现象容易造成热量堆积，最终使Cell 3中部的温度最高。在图7b区域，当气流流过Model 5的Cell 2以后，Cell 2左、右两部分气流都能顺利向下且以较快速度流入机箱底部，换热效率高，能带走电池周围更多热量，但是在Cell 2的中间小部分区域，同样由于矩形箱体阻碍气流流动，影响该区域电池散热，造成小部分区域的热量堆积，最终使Cell 2的中部也存在小范围高温区。对于Cell 1，其底部的速度矢量分布与a区域基本趋于一致，只是速度流向相反。

图7 速度矢量局部放大图

压力分布如图8所示，由于冷却气流被风机从电池箱顶部入风口泵入箱体后，高速气流首先冲击在进风口网状隔板上，少部分气流穿过孔隙直接冲击在Model 1电池组上表面，流动受到阻碍，因而此处压力最大。当气流从Model 1开始向下流动时，由于电池之间间隙均匀，电池组整体结构规整且电池模组间有竖直方向的隔板，所以气流流速均匀，压力也呈均匀变化趋势，虽然在每组电池箱体之间有一定的间隙和横梁，存在局部扰流，使截面压力有所变化，但并不影响整体电池箱压降趋势。Model 1上表面的压力平均值为483 Pa，Model 5下表面的压力平均值为185 Pa，上、下表面压差为298 Pa。

图8 X方向中截面压力云图

工况2(0～18 252 s)3个循环充放电过程中，空调不同于工况1的全程制冷，而是根据电池系统的发热情况来确定其工作状态。该工况3个循环过程中电池组的温度分布、速度矢量分布以及压力分布趋势与工况1基本一致，但是由于工况2的电池组充放电功率均小于工况1，所以电池温度相较于工况1来说较小，如图9所示。

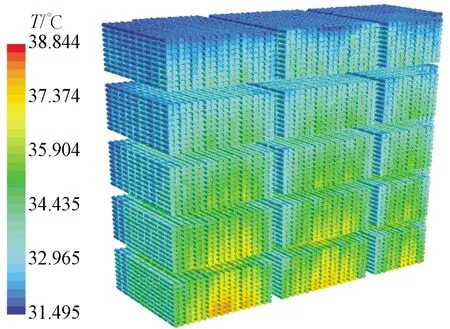
图9 Model 1-5电池表面温度分布云图(15 210 s)

根据平均温度的变化，每隔6 min对空调工作状态进行分析并调整，以循环3为例，空调工作状态随温度变化调整如图10所示：空调在226、238、250 min时温度低于35 ℃，其工作状态调整为无制冷且通风，其余时刻温度均高于35 ℃，但低于40 ℃，其工作状态调整为半制冷且通风。

从2个工况来看，虽然工况1和工况2的充放电功率与空调工作状态不一致，但二者的温度、压力等变化趋势基本相同，说明该动力电池系统即使在不同的工况下工作，也能保持其工作稳定性。

图10 循环3空调工作状况随温度变化调整曲线

2.3 实验对比

该动力电池系统在整车上进行实验，实验时环境温度尽可能接近技术规范规定的最高温度，并且在Modle 1-5的上、下表面按顺序各布置了10个监测点。选定的实验地点起始环境温度为35.2 ℃，首先将电池充电至90%SOC，然后以20%SOC～90%SOC持续循环，循环时间不少于2 h，在系统达到热平衡后停止实验，记录锂离子电池监测点的最高温度及系统内检测点的最大温差，实验结束后环境温度为36.5 ℃。2个工况结束后，最高温度及最大温差均出现在工况1 中，最高温度仿真结果与实验相比误差为3.829%，最大温差为1.25%(如表2)，二者均在工程研究所允许的范围内，表明了仿真的可靠性。

表2 仿真与实验对比

图11为工况1充电结束时Modle 1-5的表面温度分布，通过监测Modle 1-5上、下表面的温度，发现Modle 5的温度始终高于其他4个，且最高温度出现在其下表面，这与前文温度场的分析一致。

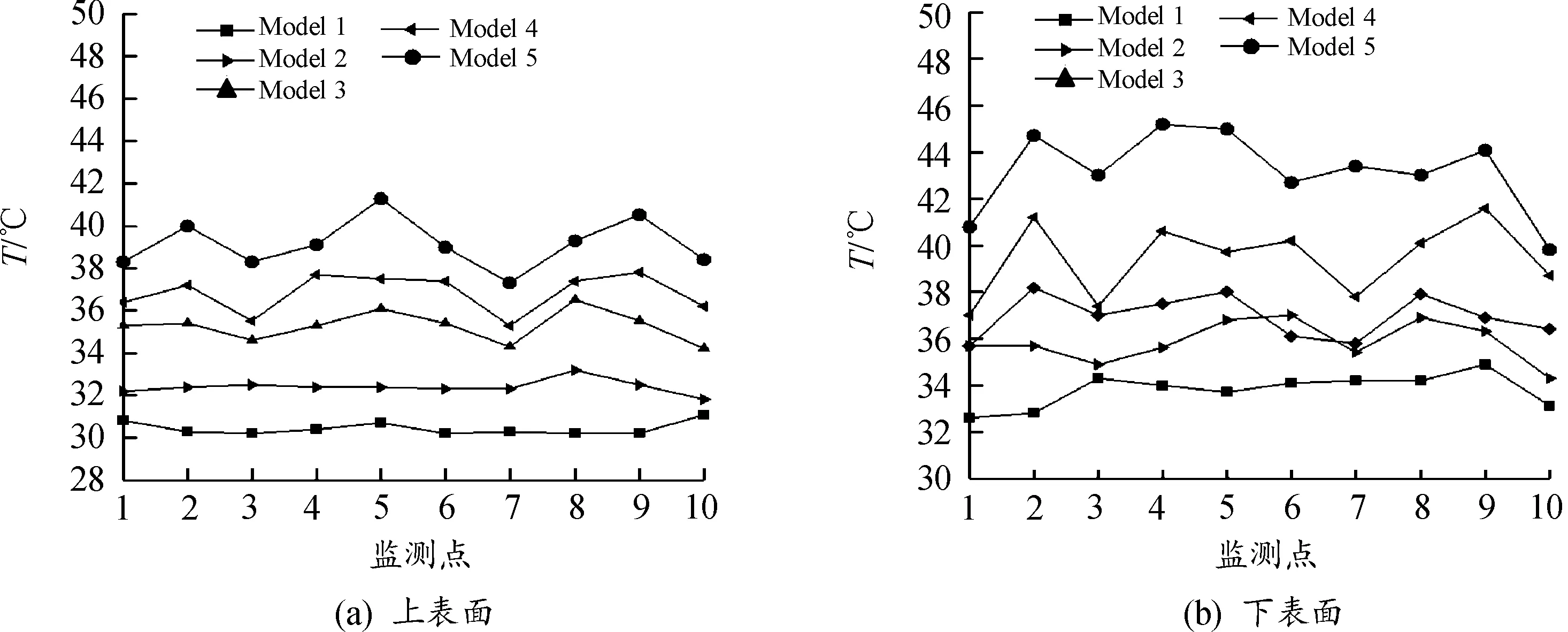
图11 Modle 1-5表面温度分布曲线

3 结论

1) 实验与仿真相结合，可以更充分、有效地观察电池的工作状态，从实验及仿真结果来看，整个电池包的均温性较好，但有些部位仍存在局部高温，设计或改进电池箱时应着重考虑这些部位的散热。

2) 电池的充放电功率越高，其工作温度也越高，在保证电池系统正常工作的前提下，可以适当降低功率。

3) 电池在高温下工作时，强制风冷的空调系统能有效保证温度在合理的范围，提高电池的寿命。为了提高空调的使用效率，可以通过设计使空调的工作状态随电池的工作温度变化而变化，这为解决电池的温度控制问题提供参考。