空气弹簧各向动刚度特性的有限元研究
李 健,李 美,谭偲龙,张少波
(1.海南大学 机电工程学院, 海口 570100; 2.湖南长城计算系统有限公司, 湖南 株洲 412000)
空气弹簧具有优良的非线性特性,其弹簧刚度随负载质量的变化而产生相应的变化,故而在不同载荷作用下,空气弹簧都能保持一个稳定的自振频率,通过改变腔体内部气压,可以使其拥有不同的负载能力,因此能适应多种载荷需要。同时空气弹簧随着载荷的变化,其结构参数也会发生具有平稳的、周期性的柔性变化,进而能够实现空气弹簧的高效控制[1]。由于空气弹簧拥有如上特点,被日益广泛的应用于火车、汽车、振动试验机、铸造机械等需要进行行程控制或减振、隔振的设备或仪器上[2]。
国外空气弹簧的发展起步较早,在1934年,工程师凡士通在福特公司研制出了空气弹簧悬架并尝试装在汽车上试验[3]。Razdan等[4-7]通过仿真分析的方式发现了气腔体积与压力的变化关系曲线,开启非线性研究的思路,建立空气弹簧有限元模型,并设置不同影响因素进行空气弹簧的动态特性分析。
国内空气弹簧研究虽在20世纪50年代已经起步,但在进入到本世纪以来才开始大规模、系统性的研究。刘增华等[8-13]利用有限元法及相关试验分别分析了空气弹簧部分参数对垂向和横向刚度特性的影响,虽然空气弹簧的非线性动力学特性已有较多研究,但主要集中于垂向或横向的单向动力学模型,且多为静态刚度特性的研究。空气弹簧的动刚度是弹簧在受到载荷动态激扰下抵抗变形的能力,而空气弹簧工作过程中通常要同时承受垂向和横向载荷,且多为动态载荷,所以对同时承受垂向和横向载荷的复合向动刚度特性进行分析很有必要。文章基于某乘用车悬架膜式空气弹簧,在ABAQUS有限元分析软件中建立空气弹簧的动态有限元模型,对空气弹簧各向动刚度特性进行分析。
1 有限元模型与非线性问题解决
1.1 空气弹簧的非线性问题
空气弹簧一般是由橡胶气囊为主体,气囊的上、下节口分别与上板盖、下板盖(底座)连接,形成一个封闭的压缩室,利用气体的可压缩性和橡胶的弹性来承受横向和垂直载荷。从实际情况出发,考虑到空气弹簧的结构和材料特性,一般认为空气弹簧有限元建模过程中存在3个非线性问题:材料非线性,构成弹簧的橡胶材料不同于金属材料的刚性特性,在受压或者拉伸情况下,材料之间的应力与位移量不成正比,即存在非线性问题;几何非线性,橡胶气囊厚度一般为3~7 mm,厚度过小则会影响系统刚度大小和性能表现,若厚度较大,则弹簧在受载时会出现大变形,非线性问题更加明显;接触非线性,建模过程中的接触问题是边界非线性问题之一。
1.2 气囊材料模型
1.2.1橡胶材料本构模型
橡胶材料是一种典型的各向异性超弹性材料,不过空气弹簧中的橡胶形变还达不到改变复合材料内部之间纤维排列的条件,所以可认为其是各向同性材料[14]。橡胶材料主要是以Rivlin模型为基础表达其应变能密度函数,其变形张量不变量级数形式表示为:

(1)
式中:Cij为力学性能常数,可通过实验测定。
由式(1)可得到各向同性材料广泛使用的Mooney-Rivlin模型,应变能函数表示为:
W=C10(I1-3)+C01(I2-3)
(2)
式中:C10和C01是与温度有关的超弹性材料参数,可通过拉伸试验拟合得到;I1和I2分别为与主拉伸系数有关的第一和第二偏应变量;本文使用的材料参数为C10=3.2 MPa,C01=0.8 MPa。当橡胶材料的变形量不足150%时,上述模型能比较全面地模拟并表述材料的力学性能,且能够达到在现实使用过程中橡胶材料性能运算的要求[15]。
1.2.2橡胶帘线层的模拟
为加强帘线的分析效果,利用 ABAQUS软件中的Rebar单元,模拟处理帘线结构。通过设定Rebar单元的弹性模量与几何特性,便可建立空气弹簧帘线层的仿真模型[16]。
1.3 单元选取与网格划分
采用HyperMesh软件对空气弹簧进行三维建模,其主要由上盖板、橡胶气囊、气体模型和底座组成。上盖板半径为170 mm;气囊高度395 mm、半径110 mm;底座高度与半径均为110 mm。并划分网格,网格单元长度选择为5 mm,采用以边界为基础划分网格。通过加大气囊与上盖板和底座发生接触部分的网格密度,可以有效提升计算精度。上盖板分为内圈与外圈2个部分,内圈为与气囊接触部分,沿边界定义100个节点,外圈定义200个节点。橡胶气囊中未与上盖板接触的上表面曲面部分,沿边界定义10个节点,气囊主体沿轴向定义60个节点。底座部分上表面与气囊接触部分同样定义100个节点,未与气囊接触的曲面部分,沿边界定义6个节点。由此划分网格,模型共16 924个节点,S4R四节点可缩减单元共 19 514个。其中上盖板5 964个单元;底座共 5 950个单元;橡胶气囊部分共7 600个单元。
1.4 材料属性与接触条件
在定义材料属性时,需要定义橡胶材料和Rebar单元的密度,方便计算橡胶气囊的集中质量;上盖板和底座需要建立实体模型,并直接定义各自的集中质量。同时在定义流体腔相互作用属性时,需要指定摩尔热容。为简化模型,接触设置设定为全局通用接触。设置橡胶气囊为主动体,上盖板和下底座为被动体。引入了多组多点约束(MPC)来使空气弹簧的各个部件连为一体,使得空气弹簧腔内形成密封环境。
1.5 分析步边界条件设置
采用ABAQUS/Explicit模块来进行动态特性计算,在显式分析步中,如果指定了非零位移,则必须添加幅值。所以将空气弹簧的分析步大体设置为3步,前2个分析步中,添加表格幅值,以平滑步的形式施加位移与初始气压。而第3分析步添加周期幅值,将上盖板参考节点的约束定义为周期变化的位移幅值。
1.5.1垂向边界条件设置
垂向特性分析共分为3个分析步:① 上盖板和底座全约束,对气囊施加气压载荷;② 保持底座全约束,上盖板施加垂向位移,使空气弹簧到达标准高度[7];③释放上盖板垂向约束,对参考点施加振幅为10 mm、频率为1~10 Hz的正弦激励。
1.5.2横向边界条件设置
横向特性分析同样分为3个分析步。其中第1、2分析步与垂向特性分析时相同。第3分析步,释放上盖板横向约束,对参考点施加振幅为10 mm、频率为1~10 Hz的正弦激励。
1.5.3复合向边界条件设置
复合向特性分析时也分为3个分析步。其中第1、第2分析步与垂向特性分析时相同。第3分析步,释放上盖板垂向与横向约束,对参考点垂向和横向同时施加振幅为10 mm、频率为1~10 Hz的正弦激励。
复合向模型位移云图如图1、2所示,由于复合向模型的特殊性,同时拥有2个方向的位移与载荷输出,此处选择上盖板参考点的等效应力(Mises)和空间位移(Magnitude)的场输出结果,位移为上盖板参考点在空气弹簧有限元模型中的实时坐标,复合向标准位置取其位移行程的中心位置。

图1 复合向模型初始位置应力云图
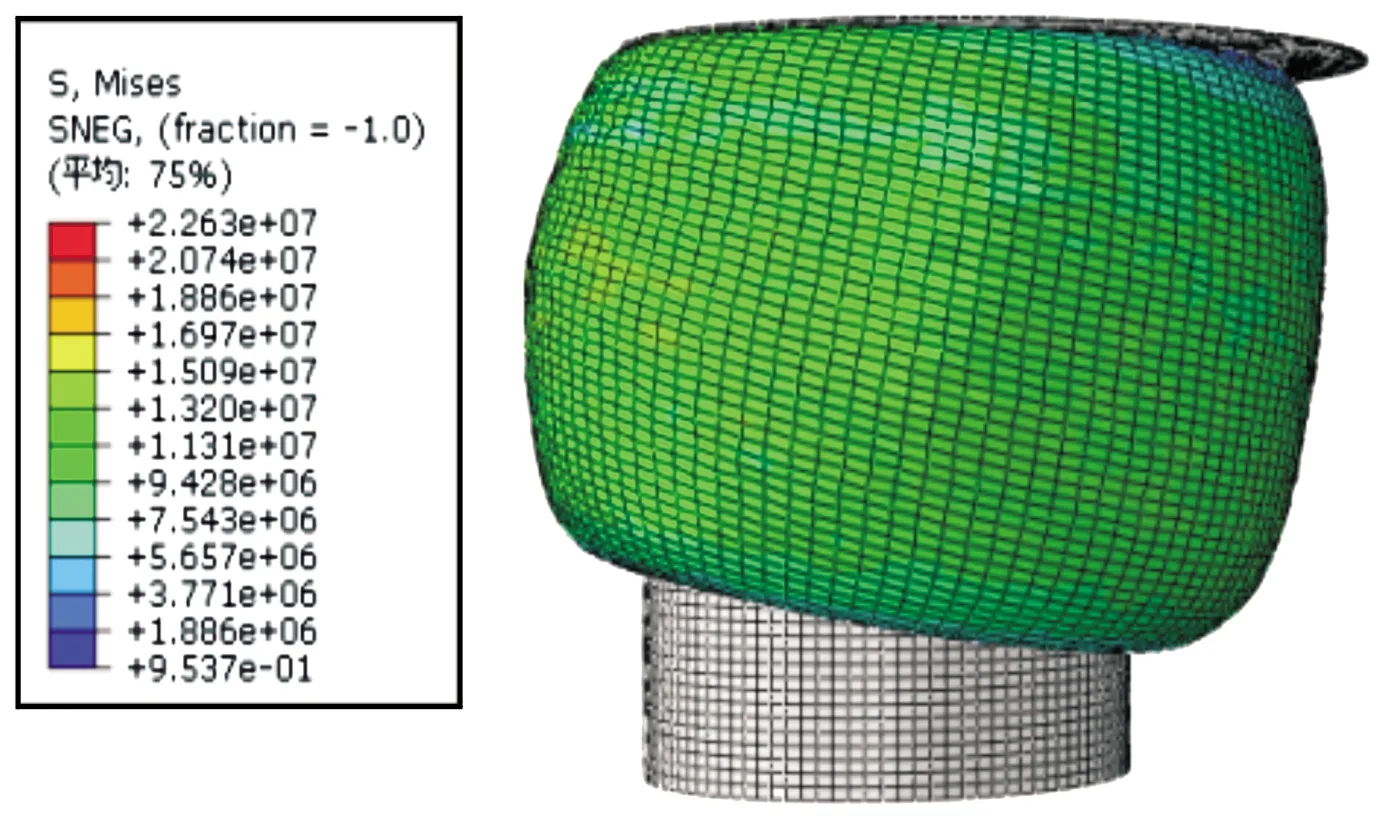
图2 复合向模型最终位置应力云图
2 动特性有限元模型试验验证
为验证上述有限元模型的正确性与可行性,根据GB/T13061—1991《汽车悬架用空气弹簧橡胶气囊》有关技术要求,在INSTRON8800数控电液伺服激振试验台上对空气弹簧进行垂向动刚度特性试验。
在实验过程中,将空气弹簧调整至标准高度(275 mm),充入初始气压,由电液伺服激振系统控制激振头对空气弹簧底部输入正弦波,最大振幅取值10 mm,激振频率范围为0.5~10.0 Hz,每次增加0.5 Hz频率,通过力传感器记录各频率下作用力-时间数据,通过位移传感器记录各频率下位移-时间数据,通过计算机数据处理拟合成作用力-位移曲线,并计算各频率下各曲线标准高度位置的动刚度。实验中共进行4组实验数据测量,采集不同初始气压值下的载荷数据。空气弹簧特性试验台架如图3所示。

图3 空气弹簧试验装置
利用有限元模型进行仿真计算,得出弹簧下底端的动载荷变化量,测得动载荷与位移通过数据处理可得到弹簧动刚度。测得弹簧动刚度试验值与仿真值如表1所示,根据参数拟合出弹簧动刚度与激振频率的关系曲线如图4所示。
比较仿真计算和试验测试得到的弹簧动刚度的数据,由表1可以看出,初始气压值越高,弹簧的动刚度特性呈现增大趋势,对于小于6 Hz的低频段,4组动刚度对比值随着激振频率增加均增加,当激振频率增加到一定范围后,动刚度变化出现不稳定现象,表示在较高工作频率下会影响动态性能表现,甚至会影响到使用寿命和使用安全性。2组数值对比分析,仿真值略大于试验值,主要是由于在有限元建模过程中,将空气弹簧内的气体设置为理想状态下的气体,把压缩过程中的摩擦简化为光滑摩擦,以及试验测量的误差等导致的。但是2种曲线的变化趋势具有一致性,数值误差也保持在一定范围内,低频段的最大误差不超过10%。总体上误差在允许范围内,表明了上述模型计算的准确性。

表1 不同条件下试验值与仿真值参数对比表
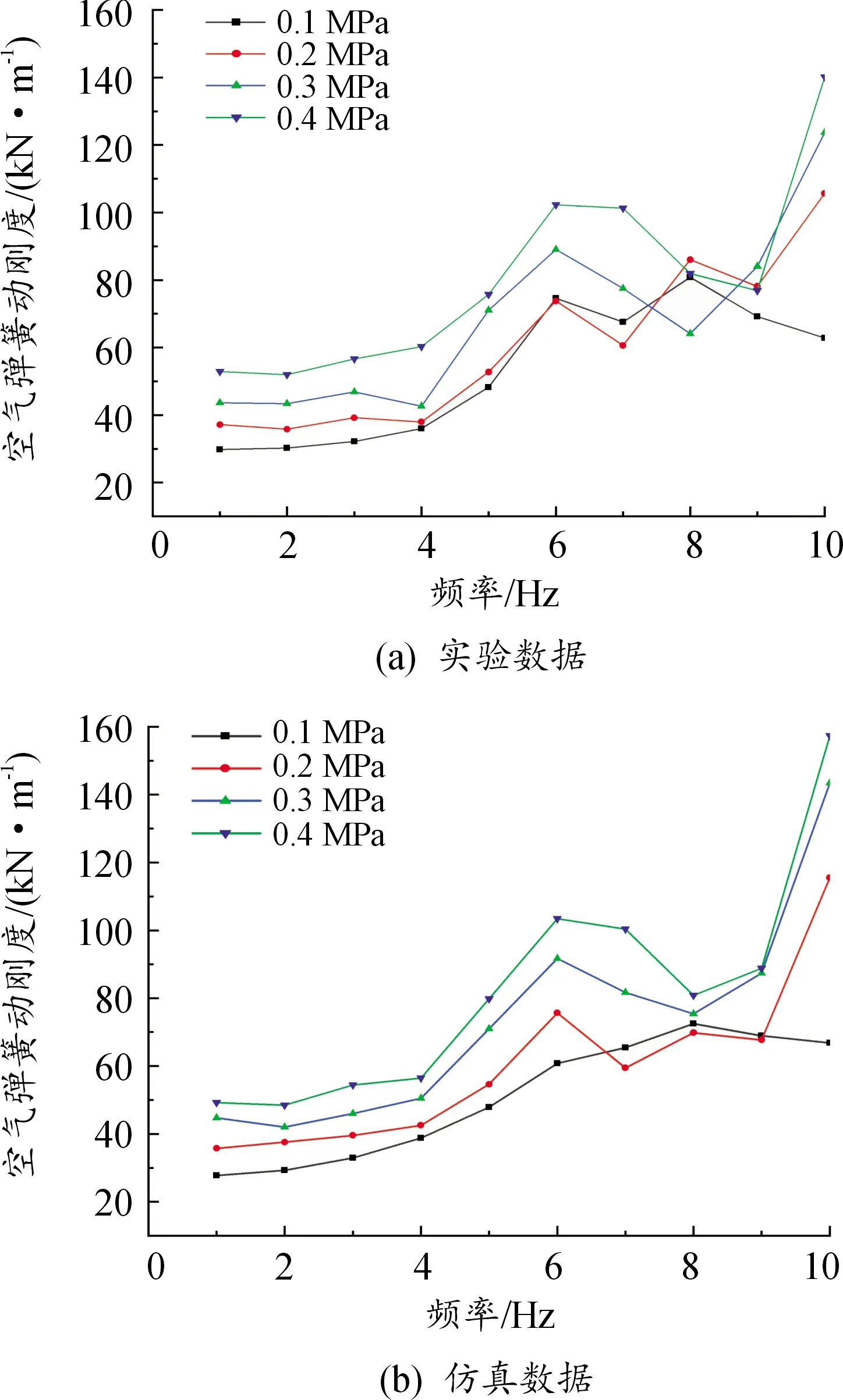
图4 弹簧动刚度与激振频率关系曲线
3 空气弹簧动刚度特性分析
分别对气囊充入0.15、0.2、0.25、0.3 MPa的初始内压。再分别按设定的分析步进行仿真计算,导出上盖板参考点的位移-时间曲线、载荷-时间曲线,并将其拟合成位移-载荷曲线,此后分别计算出各初始内压下标准高度位置的动刚度值,讨论在不同初始气压下、不同激励频率时空气弹簧标准位置处的动刚度变化特性。
3.1 不同初始内压对垂向动刚度的影响
对上盖板施加垂向正弦激励,频率范围为1~10 Hz、振幅为10 mm;各个初始内压下垂向动刚度值如表2所示,动刚度-频率曲线如图5所示。
由表2可知,激励频率从1 Hz增加到10 Hz时,当初始内压为0.15 MPa时,空气弹簧垂向动刚度上涨了9.115 kN/m;而初始内压为0.2 MPa时,动刚度上涨了11.614 kN/m;初始内压为0.25 MPa时,动刚度上涨了12.267 kN/m;初始内压为0.3 MPa时,动刚度上涨了12.397 kN/m。可见随着初始内压的增大,动刚度也随之增大。当初始内压为0.15 MPa~0.25 MPa时,初始气压对动刚度的影响增幅依次增大,而0.3 MPa时动刚度的增幅会开始减小。可见当初始气压超过一定值时,对动刚度的影响会逐渐减小。

表2 不同初始内压下垂向动刚度参数表

图5 不同初始内压下垂向动刚度-频率曲线
由图5可以看出,随着初始内压的增大,空气弹簧标准高度的动刚度也明显增大;这与空气弹簧的静刚度类似,都是因为初始内压的增大,橡胶气囊变形难度加大,气囊容积变化率变低,导致气体密度变大,从而引起空气弹簧的刚度增大。在相同初始内压下,随着振动频率的增大,标准高度的动刚度在整体呈上升趋势。在激励频率低于 5 Hz时,标准高度处的动刚度呈缓慢增加的趋势,而在激励频率高于5 Hz时,标准高度位置的动刚度会出现减小的情况,随后又开始迅速增大,而出现动刚度减小情况的频率会随着初始内压的增大而增大。
3.2 不同初始内压对横向动刚度的影响
对上盖板参考点施加横向正弦激励,频率范围为1~10 Hz、振幅为10 mm;经过数据处理拟合成动位移-载荷曲线,并通过计算得出各个初始内压下横向动刚度值如表3所示,动刚度-频率曲线如图6所示。
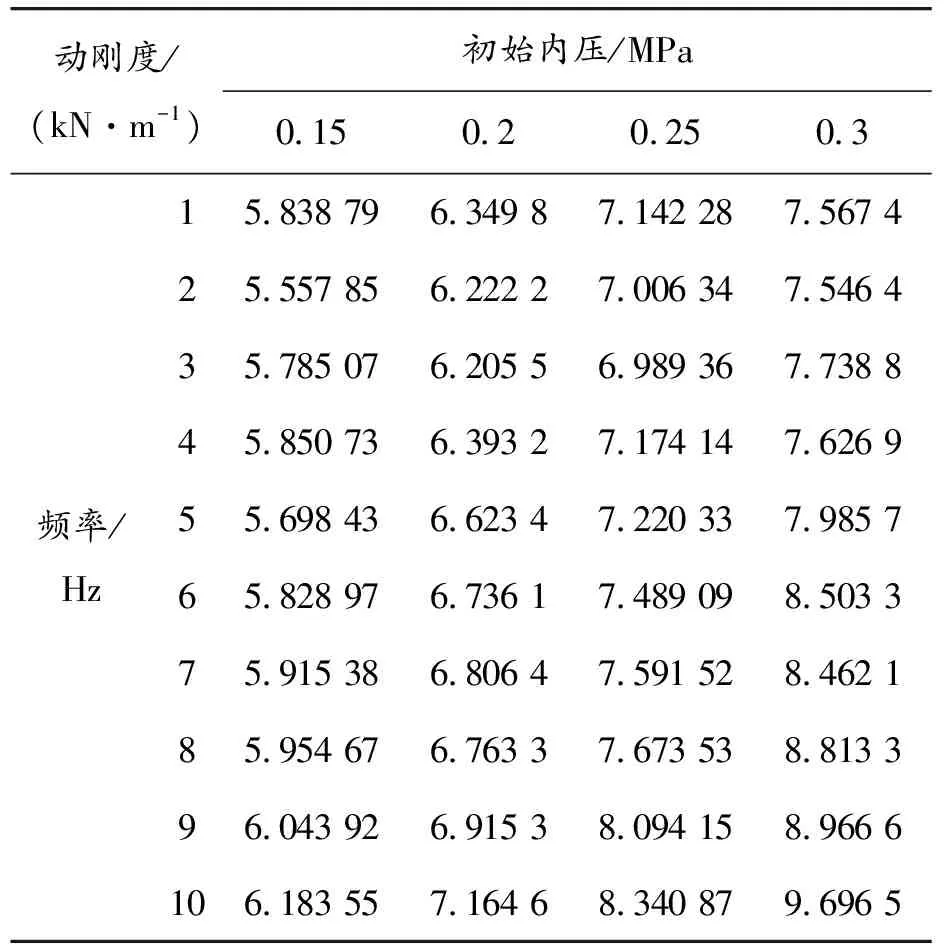
表3 不同初始内压下横向动刚度参数表
由表3可知,横向正弦激励频率从1 Hz增加到10 Hz,初始内压为0.15 MPa时,空气弹簧横向动刚度上涨了0.344 kN/m,增幅为5%;当初始内压为0.2 MPa时,横向动刚度上涨了0.814 kN/m,增幅为12%;初始内压为0.25 MPa时,横向动刚度上涨了1.198 N/m,增幅为14%;初始内压为0.3 MPa时,上涨了2.129 kN/m,增幅为28%。可见随着初始内压的增大,横向动刚度也随之增大,且随着初始内压的增大,对横向动刚度的影响也会逐渐增大。
由图6可以看出,随着初始内压的增大,空气弹簧横向动刚度也随之增大,且变化趋势具有一定的非线性特性。同时随着激励频率的增大,横向动刚度刚开始会略微减小,随后在激励频率为3 Hz时,横向动刚度开始缓慢增大,而当激励频率大于5 Hz时,横向动刚度会迅速增大。可见空气弹簧的横向动刚度在高激励频率时具有不稳定性。
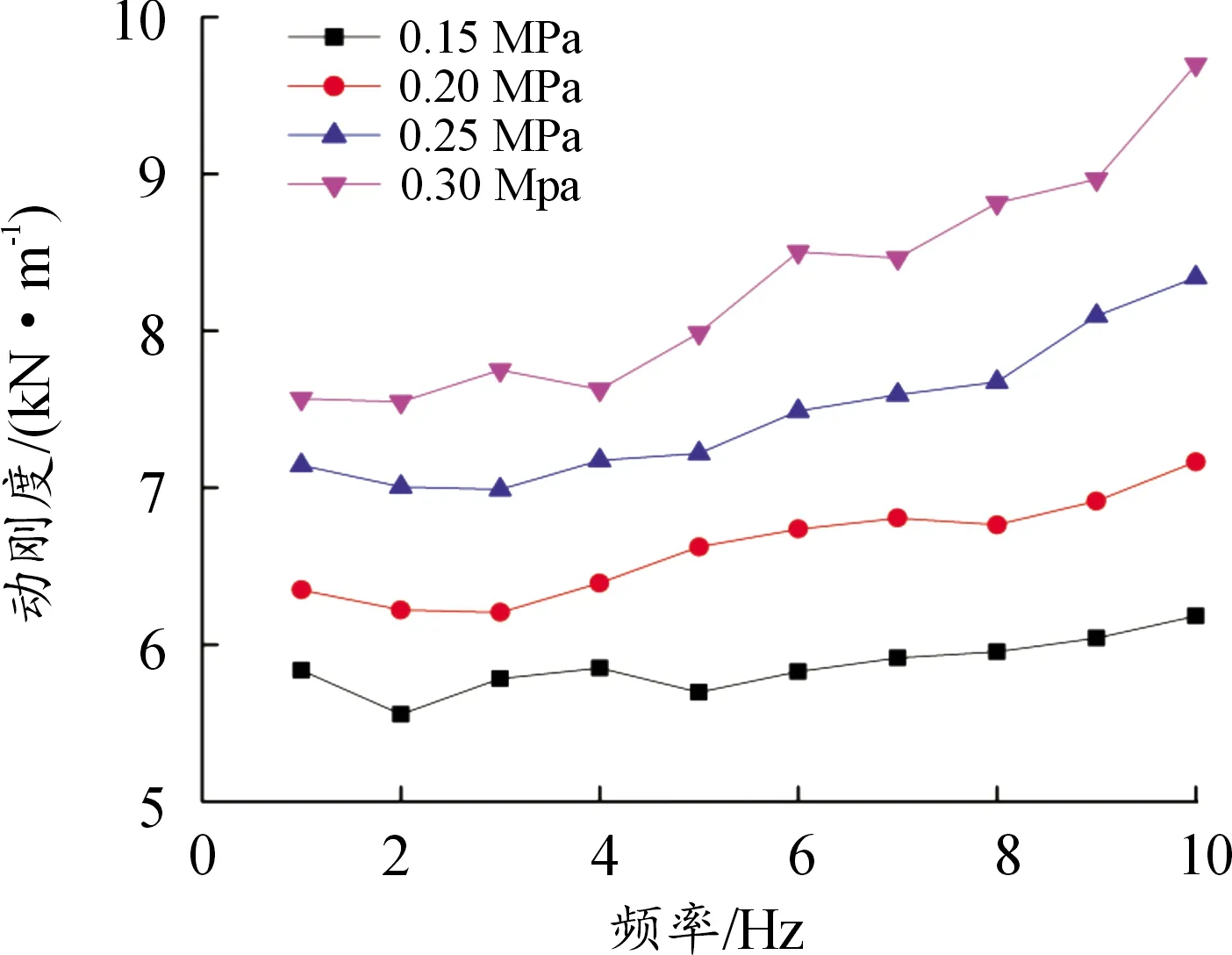
图6 不同初始内压下横向动刚度-频率曲线
3.3 不同帘线间距对静特性的影响
设定初始内压分别为0.15、0.2、0.25、0.3 MPa;对上盖板同时施加垂向和横向的正弦激励,频率范围为1~10 Hz、振幅为10 mm。经有限元计算导出上盖板参考点的等效应力(Mises)和空间位移(Magnitude)场输出结果,经过数据处理拟合成动位移-载荷曲线,并通过计算得出各个初始内压下复合向动刚度值如表4所示,动刚度-频率曲线如图7所示。

表4 不同初始内压下复合向动刚度参数表
由表4可知,当激励频率从1 Hz增加到10 Hz,初始内压为0.15 MPa时,空气弹簧复合向动刚度波动为7.122 kN/m,增幅为12%;而初始内压为0.2 MPa时,复合向动刚度波动为7.632 kN/m,增幅为9%;初始内压为0.25 MPa时,复合向动刚度波动为10.175 kN/m,增幅为10%;初始内压为0.3 MPa时,复合向动刚度波动为10.371 kN/m,增幅为8%。可见同样的随着初始内压的增大,对复合向动刚度的影响会逐渐减小。

图7 不同初始内压下复合向动刚度-频率曲线
由图7可以看出,随着初始内压的增大,空气弹簧复合向动刚度也随之增大;而在同一初始内压下,复合向动刚度整体上随着频率的增大而增大;在中频阶段,即激励频率大于3 Hz小于7 Hz时,复合向动刚度变化呈非线性;而在激励频率小于3 Hz或大于7 Hz时,复合向动刚度变化趋于线性,随着激励频率的增大而增大。
4 结论
根据超弹性材料的非线性本构关系,应用有限元软件ABAQUS,考虑了空气弹簧的材料非线性、几何非线性和接触非线性问题,建立了空气弹簧垂向、横向和复合向动态特性的有限元模型,仿真分析了空气弹簧初始内压以及激振频率对各向动刚度特性的影响。对比了动刚度仿真与试验结果,计算值与试验值比较吻合。分析结果表明:在相同激励频率下,气囊初始内压增大,空气弹簧动刚度会随着增大。而在同一初始内压下,随着激励频率的增大,垂向和横向动刚度在低频阶段呈缓慢增大趋势,在高频阶段增长较迅速且波动较大。复合向动刚度在中频阶段波动较大,而在低频和高频阶段增长较平缓且趋于线性。

