一类非线性反应扩散方程爆破解和全局解的存在性

侯春娟，李远飞

（广州华商学院 数据科学学院，广东 广州 511300）

对抛物方程和系统解的爆破现象的研究一直是人们研究的热点，出现了大量的成果[1-5].抛物方程的解当t→t*时变得无界，就称解在t*处发生爆破.通常情况下，确定解的爆破时间较为困难.因此，学者们开始估计爆破时间的界，包括爆破时间的上界和下界，参考文献［6−10］.

尤其注意到Galaktionov等研究了如下齐次Dirichlet边界条件下问题

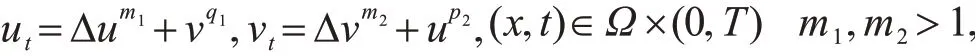
并证明了当p2q1＜m1m2时解是全局存在的；如果p2q1＞m1m2，解在有限时间爆破；当p2q1=m1m2，在一些辅助条件下解仍然是全局存在的.Lei等[11]考虑了非线性反应扩散方程

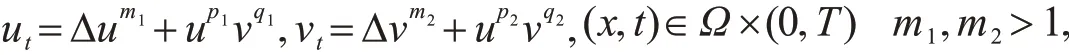
在齐次Dirichlet边界条件下全局弱解的存在性和不存在性.Payne等[12]研究了齐次Dirichlet边界条件下的问题

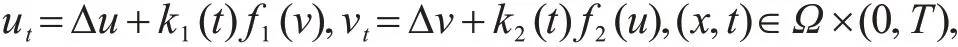
并证明了Ω⊂RN(N＞2)时，解一定在某时刻t*处爆破，获得了爆破时间的上界.当Ω⊂R2和Ω⊂R3时，文献［13］获得了爆破时间的下界.李远飞[13]研究了方程

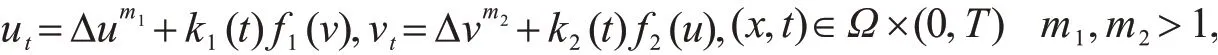
在齐次Dirichlet边界条件下解的爆破现象，并获得了爆破时间的上下界.当方程的初始条件满足一定约束条件时，证明了解是全局存在的.Shen等[14]把文献［13］的研究推广到了非线性边界条件

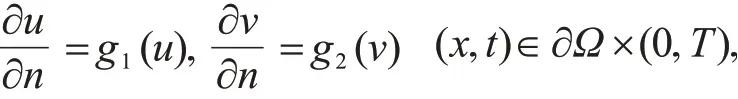
利用Sobolev不等式和微分不等式技术，获得了爆破时间的上界和下界.

文献［15］考虑了齐次Dirichlet边界条件下方程

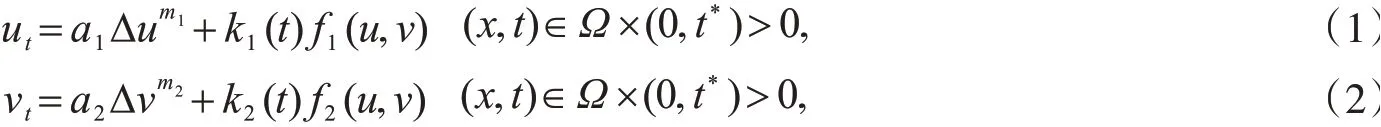
其中，m1，m2≥1，Ω⊂RN(N≥2)，k1(t)，k2(t)是大于零的连续函数，a1，a2＞0是扩散系数，f1，f2是连续的非负函数，t*是可能的爆破时间.该模型主要模拟了一些2种物质的燃烧过程或传输扩散过程[15-16]，m1，m2＞1时表示慢扩散，m1=m2=1时表示线性扩散.文献［15］利用上解法等方法得到了证明了弱解存在唯一性，又证明了全局解的存在性和不存在性，明确了域系数和几何形状对全局解存在性的影响.在此基础上，研究了所有维空间域爆破时间的界.文献［17］研究了具有空变系数的混合抛物系统

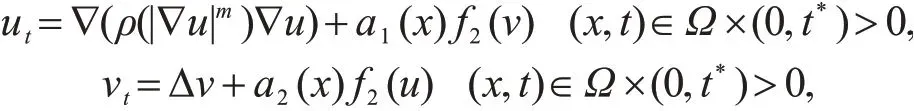
在非线性边界条件下的爆破问题，利用能量估计的方法得到了爆破时间的下界.更多关于解爆破性研究和解的存在性研究的最新成果参考文献［18−24］.

研究方程（1）和（2）在Ω⊂R3上解的存在性及爆破现象.考虑以下非线性边界条件

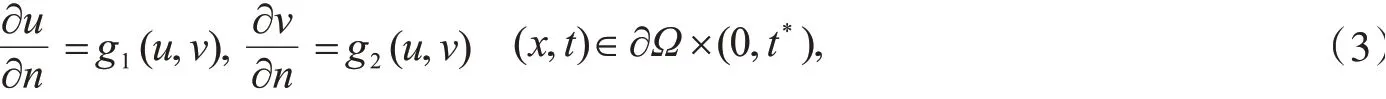
其中，g1，g2是非负的连续函数.该边界条件表示2种物质在燃烧时和外界发生了热交换，在边界上并非绝缘.

利用能量分析法和微分不等式技术，得到了爆破时间的上界以及证明了全局解的存在性，利用Sobo⁃lev不等式解决边界条件带来的困难.此外，模型（1）和（2）满足以下初始条件

其中，非负初始数据u0(x)，v0(x)是满足相容性条件的C1函数.因此，根据经典抛物理论，问题（1）~（4）的解是唯一存在的，并且是非负的.

研究方程（1）~（4）的解一定在某有限时刻t*处爆破的条件，并推导爆破时间的上界.假设λ1是问题

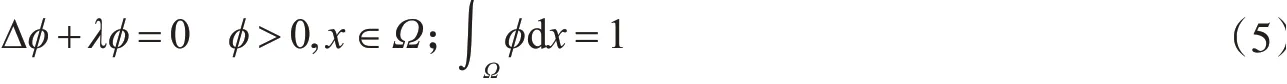
的第一特征值.而f1，f2满足

通过构造一个与φ相关的辅助函数，获得了爆破时间的上界，其优点是不需要g1，g2满足额外的条件.当式（6）不再成立时，此时假设f1，f2满足一些不同的约束条件，证明解是全局存在的.

1 爆破解

证明方程（1）~（4）的解在某有限时刻爆破，并估计爆破时间的上界.为此，构造辅助函数

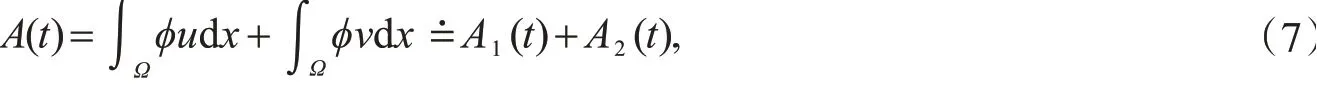
其中，φ的定义见式（5）.

可以得到以下定理：

定理1设(u，v)是非线性方程（1）~（4）在Ω⊂R3上的非负经典解.函数f1，f2满足式（6），不失一般性，假设p1≥q1.函数k1(t)，k2(t)满足

且初始数据u0和v0满足一定的约束条件.则方程（1）~（4）的解在A(t)的测度下必在有限时刻t*处爆破.具体地，当p1=q1时，若u0和v0满足

则t*满足t*≤T1，其中，

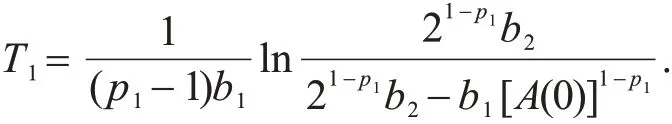
当p1≠q1时，若u0和v0满足

则t*满足t*≤T2，其中，

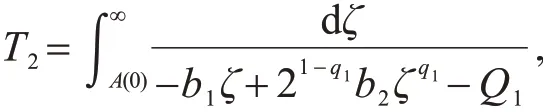
其中，

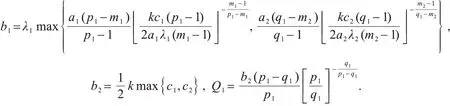
证明利用方程（1）~（4），散度定理，式（5），（6）和（8）对（7）求导可得

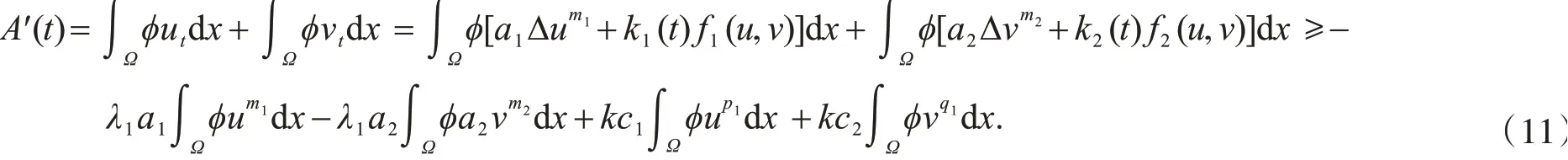
利用Hölder不等式和Young不等式，可得

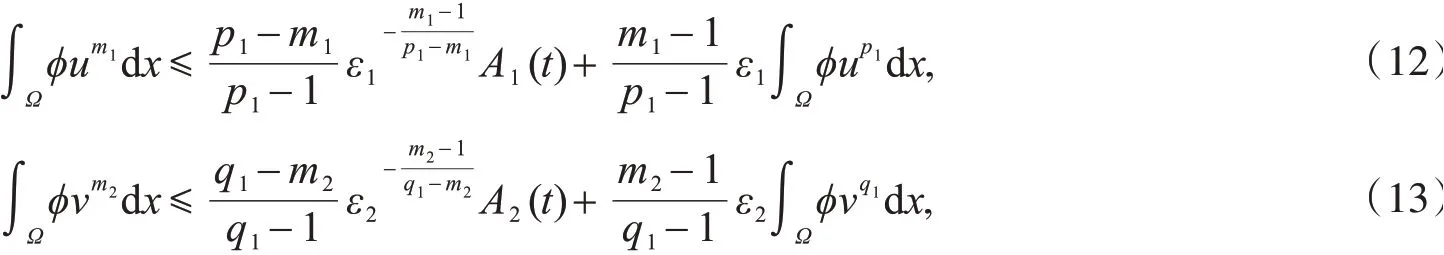
其中，ε1，ε2是大于零的任意常数.令

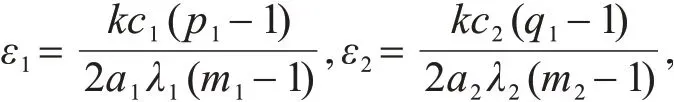
再把式（12）和（13）代入到式（11），可得

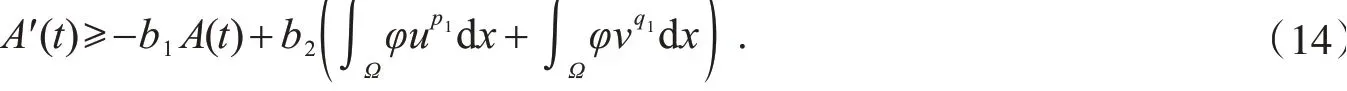
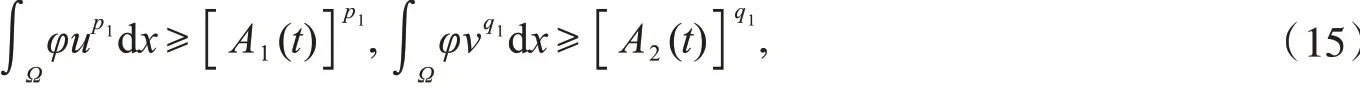
联合式（14）和（15），可得

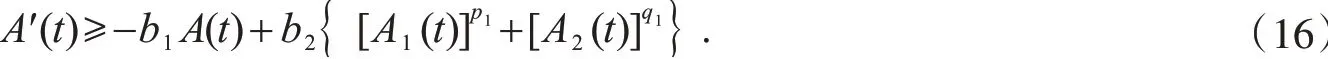
Ⅰ 当p1=q1时，利用数学不等式

则

把式（18）代入到式（16），可得

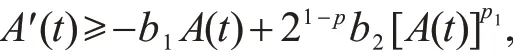
即

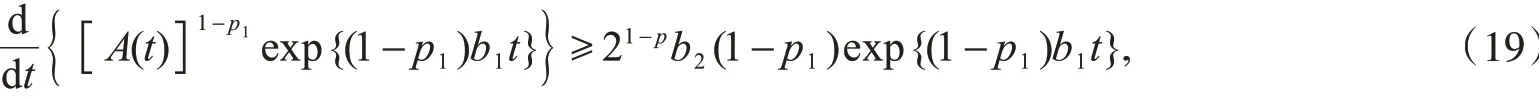
对式（19）从0到t积分，可得

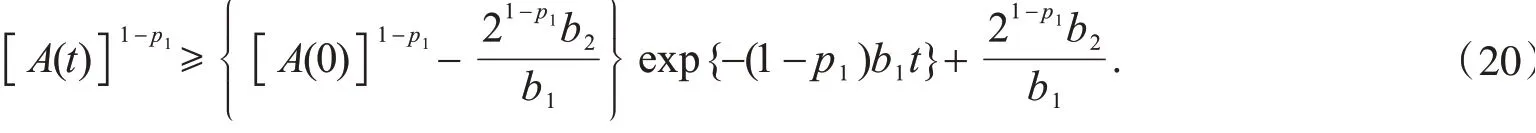
由于初始数据u0和v0满足式（9），则当t=T1时，式（20）右边的部分等于零.又由于p1＞1，所以方程（1）~（4）的解必在t*＜T1处爆破.

Ⅱ 当p1≠q1时，利用Young不等式，可得

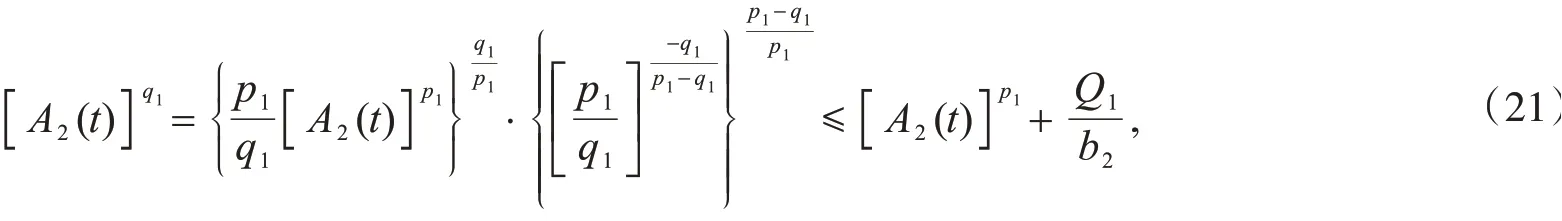
把式（21）代入到式（16），可得

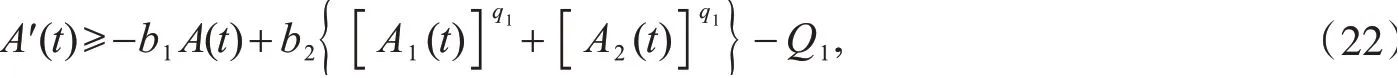
再次利用式（17），由式（22）可得

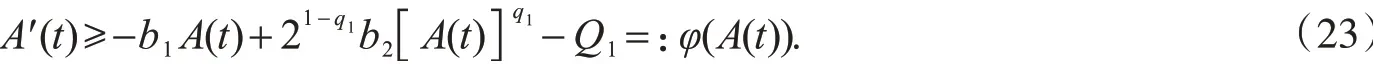
由于初始数据u0和v0满足式（10），则φ(A(0))＞0.由式（23）可知：存在t1＞0使得A′(t)≥0，t∈[0，t1]，所以A(t1)≥A(0).由于q1＞1，所以φ(A(t))是A(t)的递增函数，所以φ(A(t1))≥φ(A(0))＞0.同理存在t2＞t1，使得φ(A(t2))≥φ(A(t1))＞0.如此下去，可得φ(A(t))＞0，∀t＞0.由式（23）可知A′(t)＞0，∀t＞0，说明A(t)一定在某有限时刻t*处爆破.由式（23）可得爆破时间的上界.

证毕.

注1 由式（9）和式（10）可知，解一定发生爆破的条件是要求初始数据充分大，定理1得到了爆破时间的上界.

注2 与文献［15］相比，增加了对初始条件的要求，对边界条件没有增加限定，即本文把文献［15］的研究推广到了非线性边界条件的情形.

2 全局解

首先给出以下引理.

引理1［25］设Ω是RN(N≥2)上的有界星型区域.若w∈C1(Ω)，则有

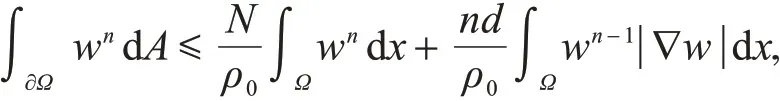
其中，ρ0=min∂Ω(x，n)，d=max∂Ω|x|，n＞1.

引理2［26］设Ω是RN(N＞2)上的有界星型区域，则存在一个依赖于Ω和N的常数Λ1＞0，使得

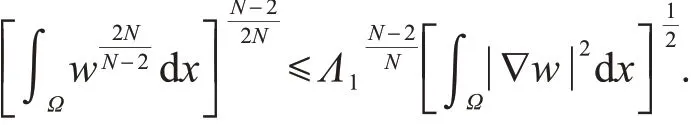
利用引理2，可得

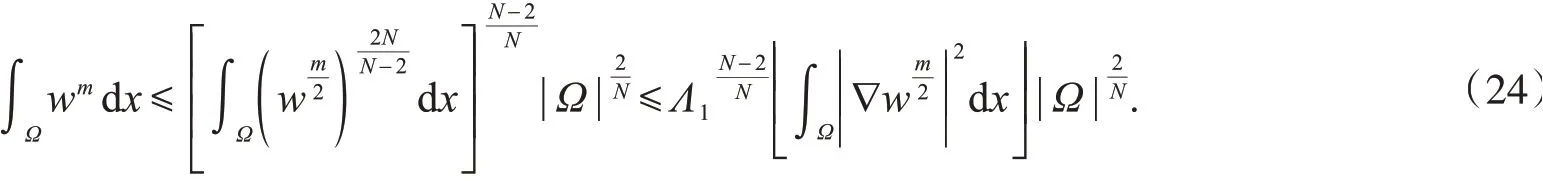
由式（24）可得以下引理.

引理3 设Ω是RN(N＞2)上的有界星型区域，则有

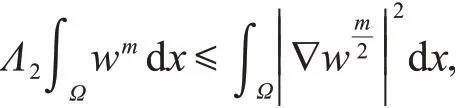
建立以下辅助函数

其中，α是一个待定的大于零的常数.

可以得到以下定理.

定理2设u和v满足是方程（1）~（4）在Ω⊂R3上的非负解.函数g1，g2满足

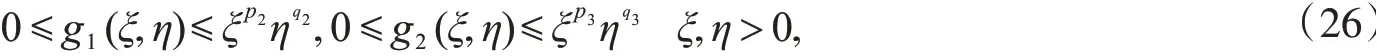
其中，0＜p i+qi≤1，m1+2(p i+qi)＞3，i=2，3.函数f1，f2满足式

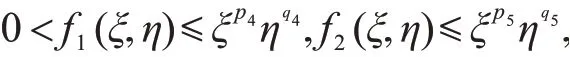
其中，0＜p4+q4≤1，p5+q5≤1.则方程（1）~（4）的解在有限时刻不会发生爆破，即方程（1）~（4）具有全局解.

证明首先在式（25）取

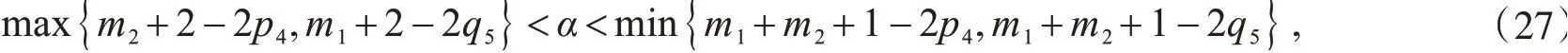
由于0＜p4+q4≤1，p5+q5≤1，式（27）表明α+m1＞2q4，α+m2＞2q5.

对B(t)求导，再利用散度定理，式（25）和方程（1）~（4），可得

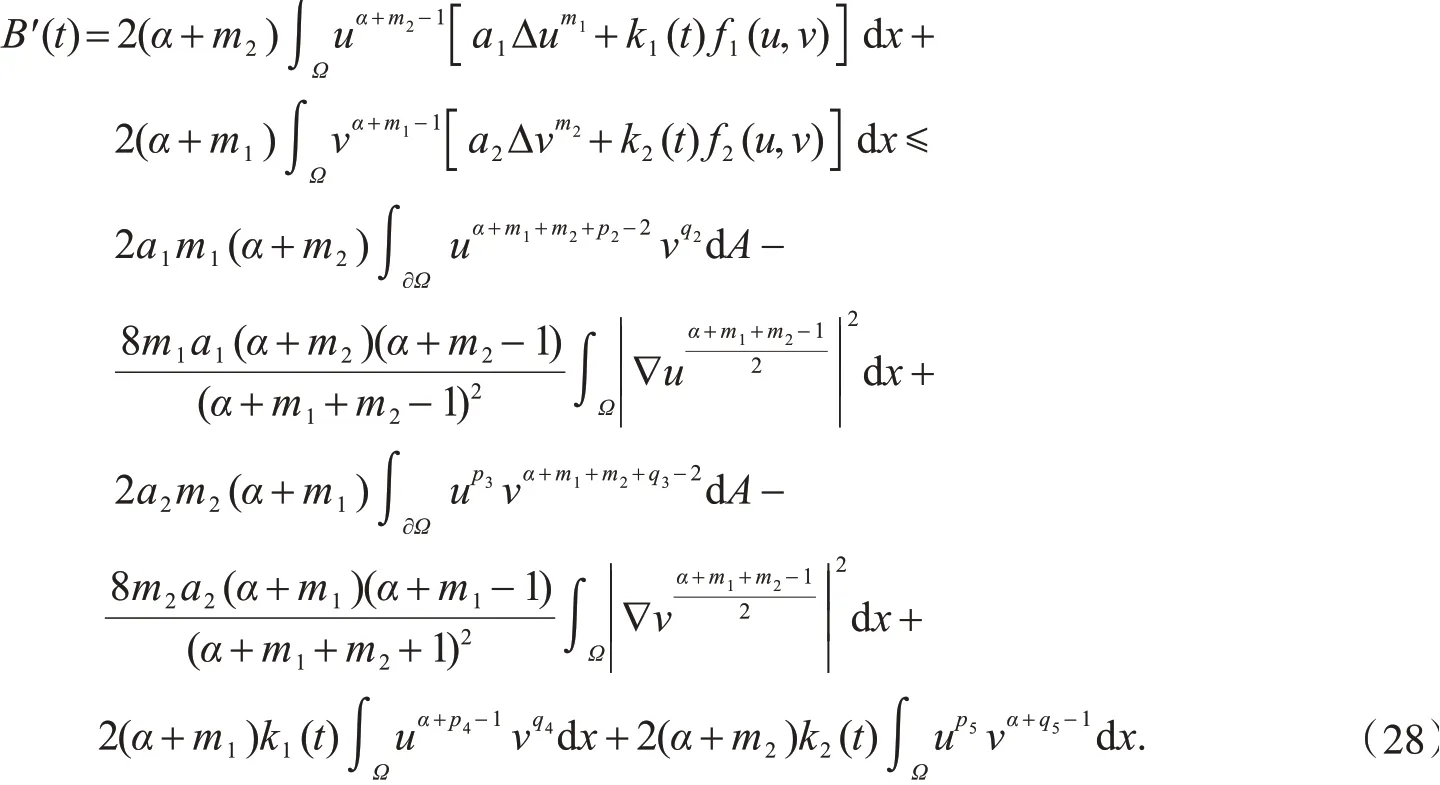
利用Hölder不等式和Young不等式，可得

利用引理1和Hölder不等式，可得

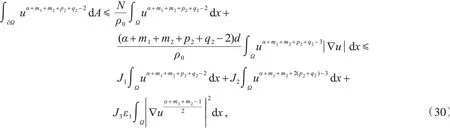
其中，ε1是大于零的任意常数以及

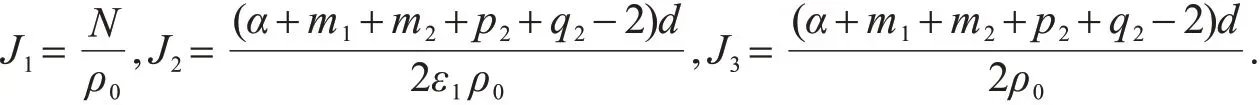
类似地，有

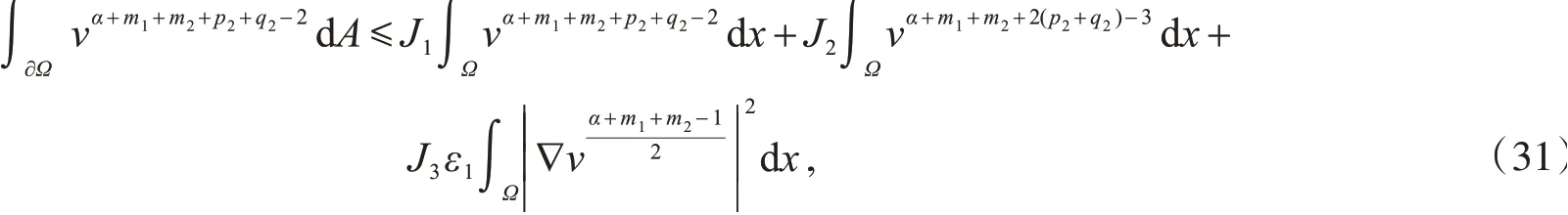
把式（30）和（31）代入到式（29），可得

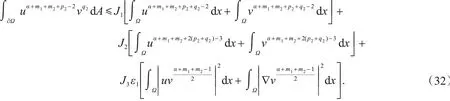
类似地，有

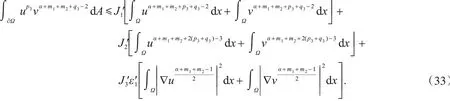
处理式（28），利用Hölder不等式，Young不等式和引理2可得

其中，ε3是大于零的任意常数以及

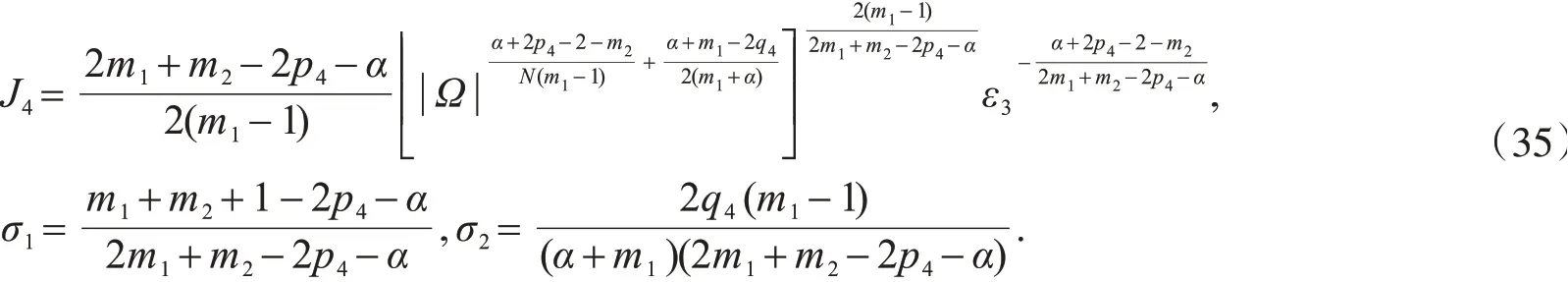
类似地，有

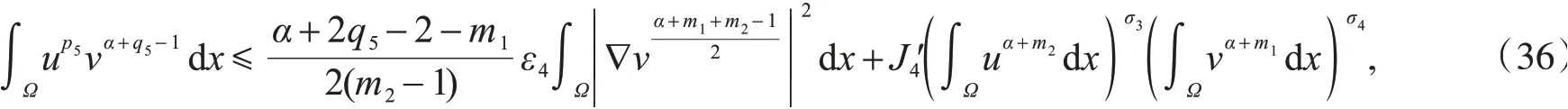
其中，ε4是大于零的任意常数以及

取适当的ε1，ε′1，ε′3和ε′4，使得

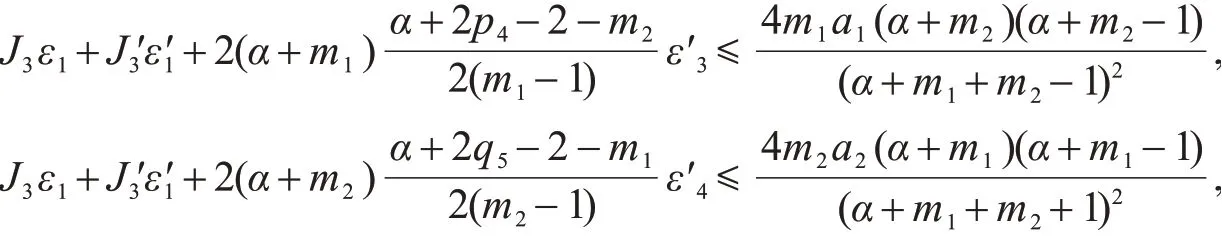
再把式（32）~（36）代入到式（28），可得

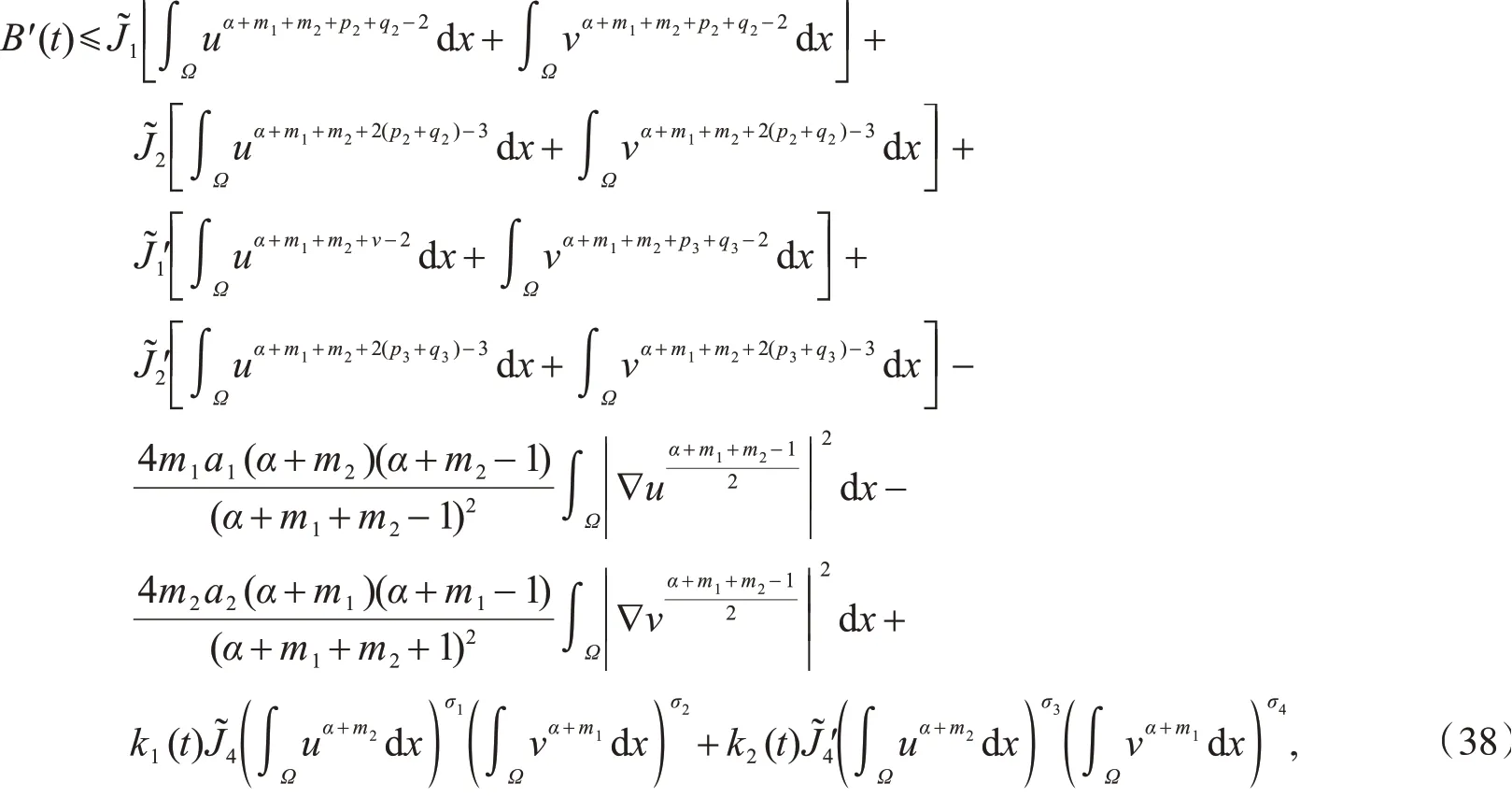
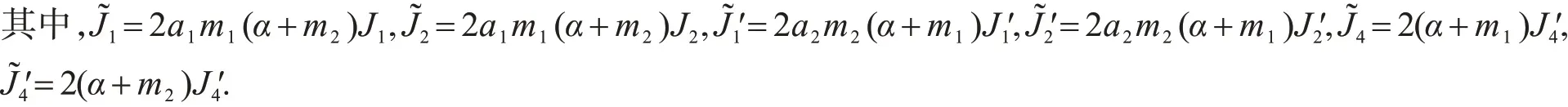
利用H ölder不等式，Young不等式，可得

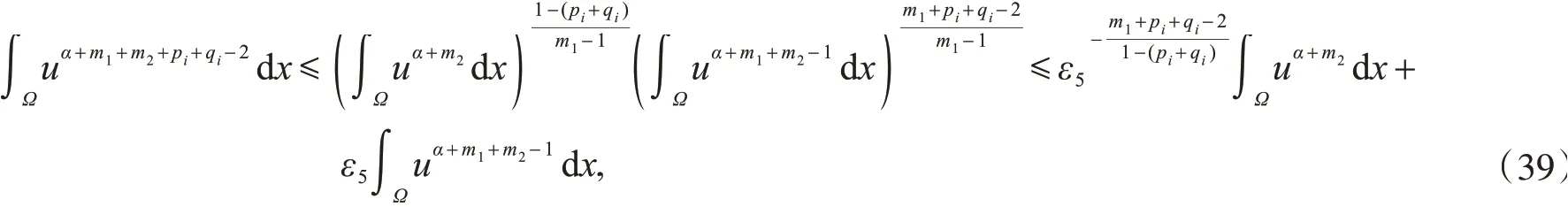
其中，ε5是大于零的任意常数，i=2，3.类似地，有

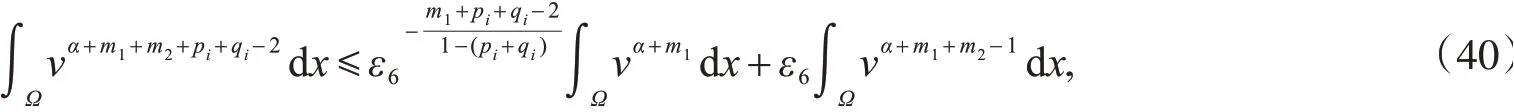
其中，ε6是大于零的任意常数.类似地，有

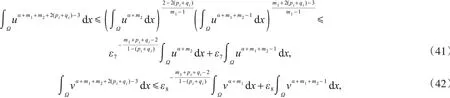
其中，ε7，ε8是大于零的任意常数.在引理3中，取m=α+m1+m2-1，w=u，v，可得

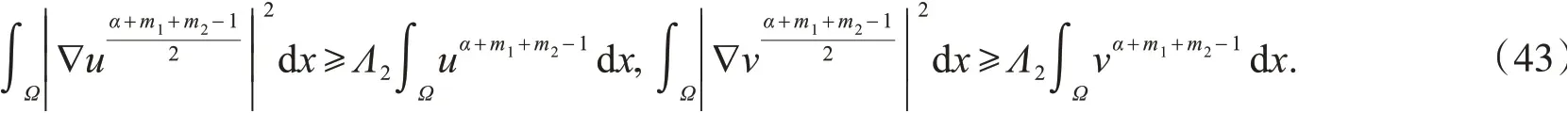
现取εi，i=5，6，7，8满足

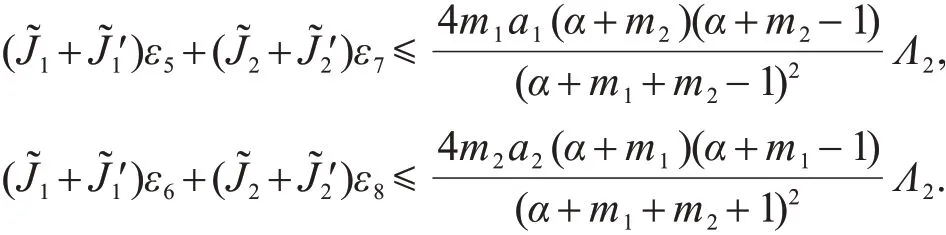
再结合式（38）~（43），可得

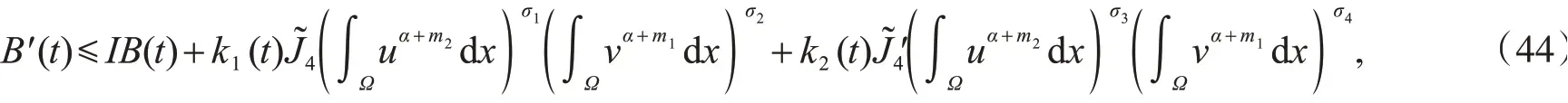
其中，I是大于零的常数.注意到

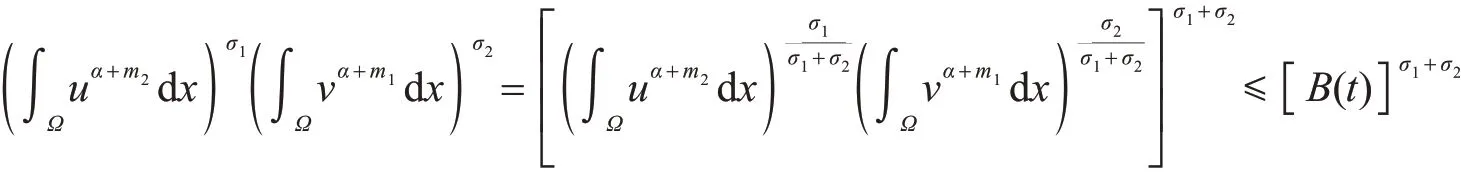
和

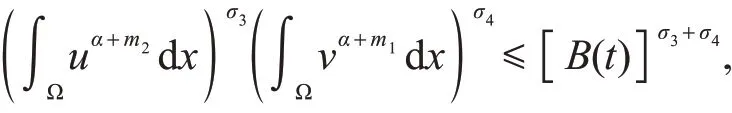
并结合式（44），可得

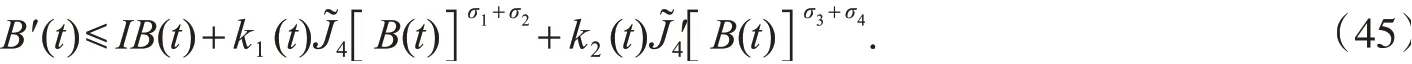
令k(t)=max{1，k1(t)，k2(t)}，则由式（45）可得

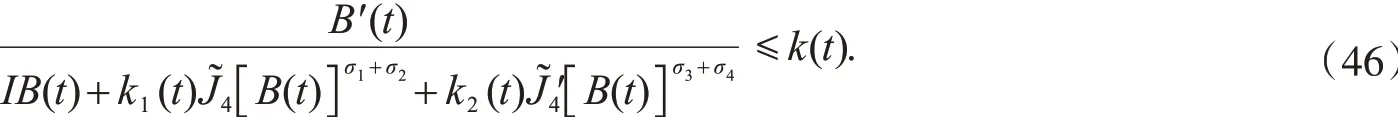
如果方程的解在某有限时刻t*发生爆破，则对式（46）从0到t*积分，可得

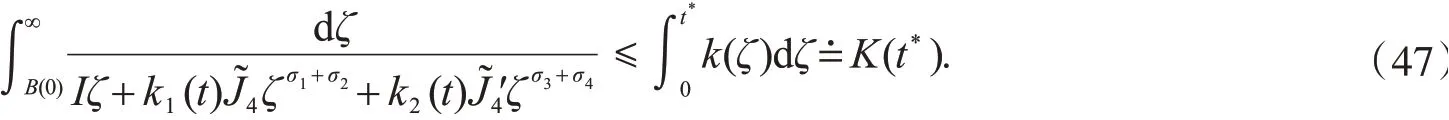
因为α+m1＞2q4，α+m2＞2p5，由式（35）和（37）可知

于是式（47）左边的积分发散，而K(t*)是t*的单调递增函数，所以t*=∞.因此在B(t)测度下，解不可能在任何有限时间爆破，即解是全局存在的.

注3 本文限定方程中的参数0＜p i+qi≤1，i=2，3，实际上是控制了在边界上物质与外界发生热交换的程度，因此得到了全局解.

注4 通过对边界条件做出一定限制，得到了与文献［15］类似的结论，这也是对文献［15］的推广.

注5 如果方程（1）和（2）由以下带梯度项的抛物方程代替

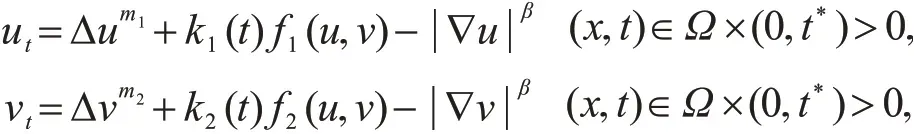
只要对β进行适当的限定，定理1和定理2仍然成立.

3 小结

研究了具有非线性边界条件下当N=3时非线性反应扩散方程，通过对方程中的参数进行一定的限制，得到了爆破解和全局解的存在性，同时本文的方法还可以向更一般化的模型推广.