基于信息干预下HBV传染病模型稳定性分析与最优控制

张靖文，王浩华，2，3

（1.海南大学 理学院，海南 海口 570228；2.海南大学 海南省工程建模与统计计算重点实验室，海南 海口 570228；3.海南大学 热带特色林木花卉遗传与种质创新教育部重点实验室，海南 海口 570228）

流行性传染病的爆发不仅会导致大规模的死亡，而且会影响社会稳定，严重影响经济和生活，因此，研究流行性传染病的传播动力学模型，在预测传染病的动向和阻断其传播病源等方面至关重要［1−6］.乙肝病毒（HBV）通过血液传播、母婴传播、无保护性行为传播等方式感染肝脏细胞，诱发炎症，从而引起多种疾病［7］.据世界卫生组织报告，全球约有20亿人携带乙肝病毒，约200万人患有慢性肝感染，每年超过78万人因此死亡［8］.

如何有效预防和控制乙肝的传播是关心的热点问题之一.目前，众多研究者基于传染病模型对HBV的传播动力学及相关性质进行了深入的研究.Khan等［9］在考虑疫苗接种因素下，对HBV传播的阻断进行了定量研究；Zhao等［10］研究表明，有效的信息干预手段（包括媒体宣传，病例教育等），可以有效降低感染人数峰值；Bao等［11］分析了环境噪声对随机HBV感染模型传播动力学的影响，并提出了干预策略；Wang等［12］研究具有细胞间传播和免疫应答的随机HBV感染模型，分析了疾病了灭绝和持续性存在的条件.笔者考察了有效疫苗接种率以及信息干预下的HBV传染病模型，给出了新模型平衡点的局部和全局稳定性的充分条件及参数的动力学特性.此外，为了控制HBV的传播，添加了信息传播状态变量，再利用最优控制方法建立了基于疫苗有效率、信息反应强度以及有效治疗率的多维控制动力学模型，在论证最优控制存在的基础上，通过数值模型验证的相关理论结果.

1 模型建立

为了有效控制疾病的传播，将建立一个带有疫苗接种和信息干预的HBV传染模型来研究疾病的传播动力学.

首先，Khan等［9］基于疫苗接种率提出了HBV的传播动力学模型

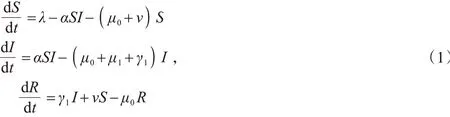
其中，S(t)，I(t)，R(t)分别代表易感人群，感染人群和恢复人群，λ代表出生率，α代表从易感人群到感染人群的转移概率，μ0代表自然死亡率，μ1代表疾病导致的死亡率，γ1代表感染人群的治愈率，v代表疫苗接种率.Khan等将总人口划分为3类：易感人群，感染人群和恢复人群.新出生的孩子都为易感人群，易感人群与感染人群接触会以一定的比例转移到感染人群中，易感人群接种疫苗会转移到恢复人群中，3种人群都有固定的自然死亡率，感染人群有疾病导致的死亡以及被成功治疗转移到恢复人群中，恢复人群都有永久免疫力.

再考虑有效信息干预，得到如下带有信息干预和疫苗接种的HBV传染病模型（图1）

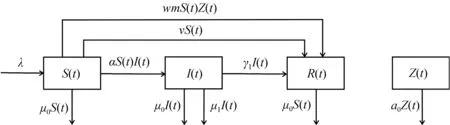
图1 模型（2）示意图

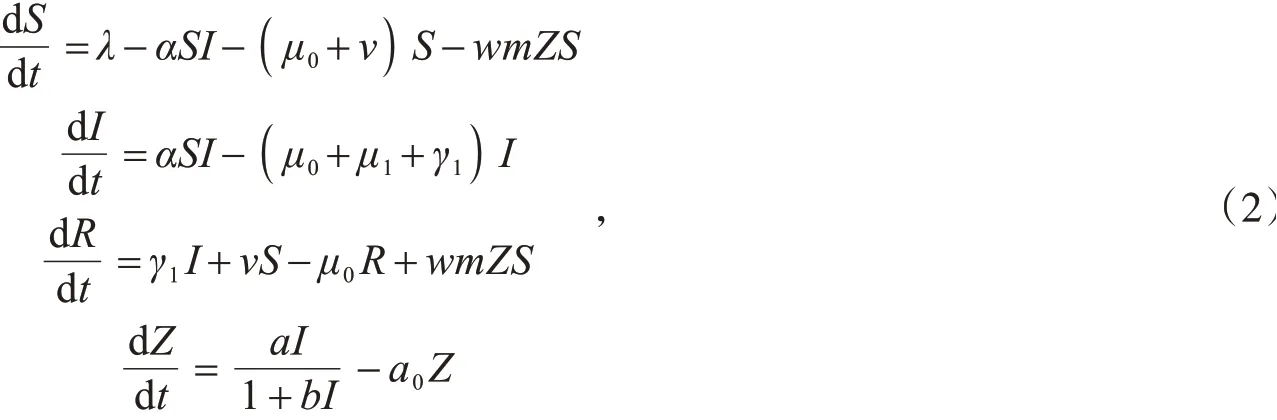
其中，Z(t)表示信息密度，m表示信息干预率，w表示信息的反应强度，a表示信息的增长率，b表示饱和常量，a0表示信息的自然衰退率.

2 模型平衡点与基本再生数

计算模型（2）的平衡点以及基本再生数，是研究其传播动力学的基本步骤.基本再生数R0定义为患病期内病人传染致病的平均人数.根据文献［13］中的方法，模型（2）的基本再生数为

令模型（2）所有方程右端为0，可得模型（2）的2个平衡点：

a无病平衡点

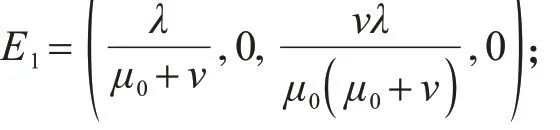
b疾病平衡点

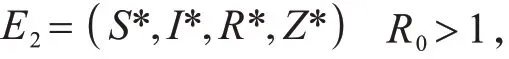
其中，

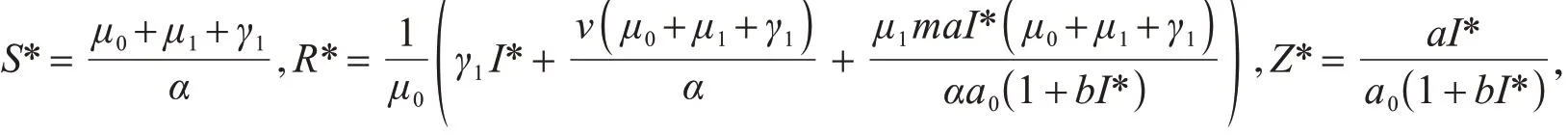
I*为下列方程的正根

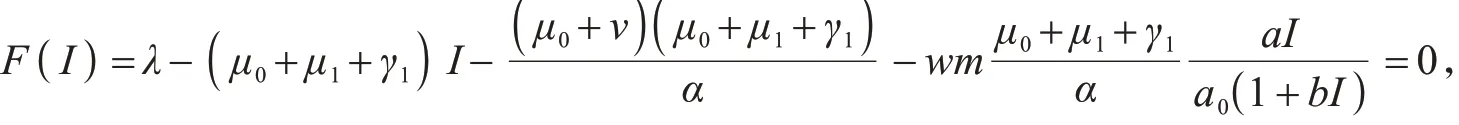
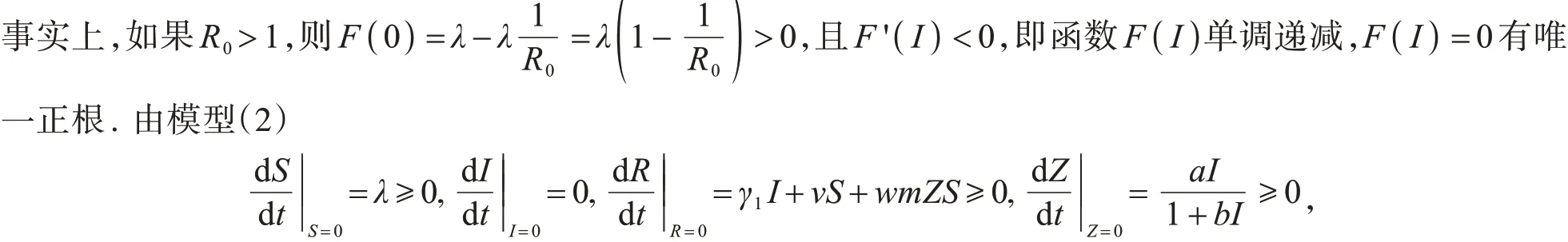
即模型（2）的所有解都是非负的.

令总人口N=S+I+R，由模型（2）可知

因此，得到不变集Γ，

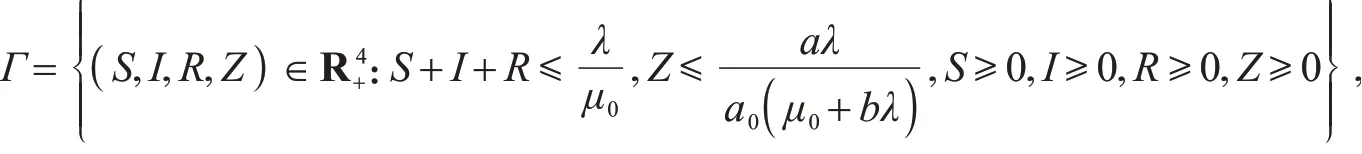
3 平衡点分析

探讨了模型2个平衡点的局部稳定性，分叉和全局稳定性，此外还对模型的参数进行了局部敏感性分析.

3.1平衡点的局部稳定性模型（2）的变分矩阵为

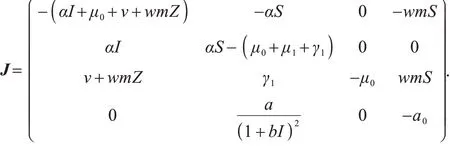
定理1

1）若R0＜1，模型（2）的无病平衡点E1是局部渐进稳定的；若R0＞1，则E1不稳定.

2）若R0＞1，则模型有唯一的疾病平衡点E2，此外，若A1B1＞C1且A1(B1C1-A1D1)＞C21，则E2是局部渐进稳定的.

证明

1）计算变分矩阵J在无平衡点E1的特征值为

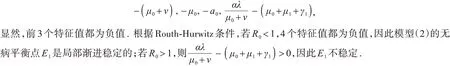
2）计算变分矩阵J在疾病平衡点E2的特征方程为

3.2分叉

引理1［15］考虑下列带参数φ的ODE方程

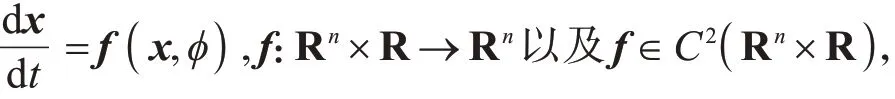
其中，0是系统的稳定点，对任意φ都有f(0，φ)=0.假设fk是f的第k个分量，并且

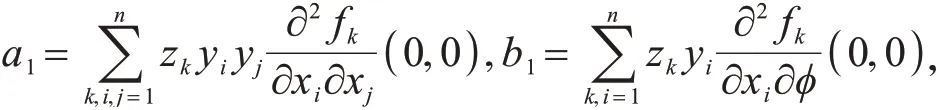
其中，y，z分别表示特征值0的右特征向量和左特征向量，上述系统在0附近的局部动力学完全由a1，b1决定.

1）a1＞0，b1＞0.当φ＜0并且|φ|≪1时，0是局部渐进稳定点，并且存在一个正的不稳定的平衡点；当0＜φ≪1时，0是不稳定点，并且存在一个负的局部渐进稳定平衡点.

2）a1＜0，b1＜0.当φ＜0并且|φ|≪1时，0是不稳定点；当0＜φ≪1时，0是局部渐进稳定点，并且存在一个正的不稳定平衡点.

3）a1＞0，b1＜0.当φ＜0并且|φ|≪1时，0是不稳定点，并且存在一个负的局部渐进稳定平衡点；当0＜φ≪1时，0是稳定点，并且有一个正的不稳点平衡点.

4）a1＜0，b1＞0.当φ从负值变化到正值时，0从稳定点变成不稳定点.相应地一个负的不稳定平衡点变成正的并且局部渐近稳定点.

定理2当R0=1时，模型（2）有一个前叉分支.

证明令x1=S，x2=I，x3=R，x4=Z，再令φ=α为分支参数.在φ=φ*=α*，由R0=1可以推出α*=模型（2）可以重新写成

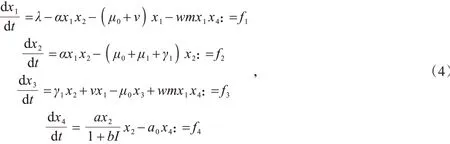
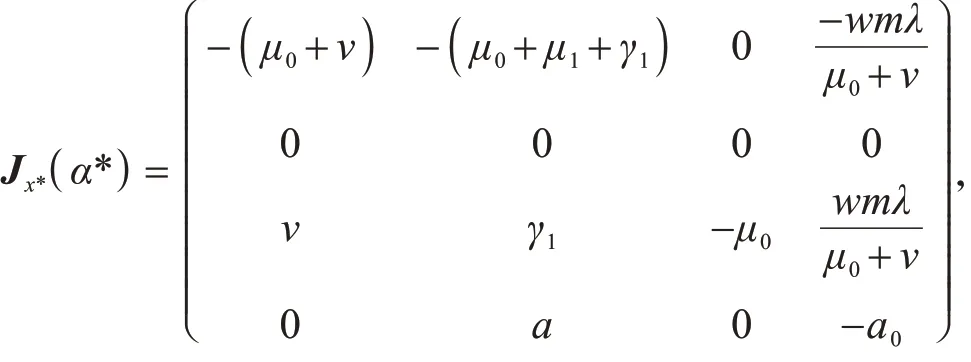
显然，当R0=1时，J x*(α*)有一特征值为0，并且其他特征值都非负，矩阵J x*(α*)对应于特征值0的右特征向量为y=(y1，y2，y3，y4)＇，其中

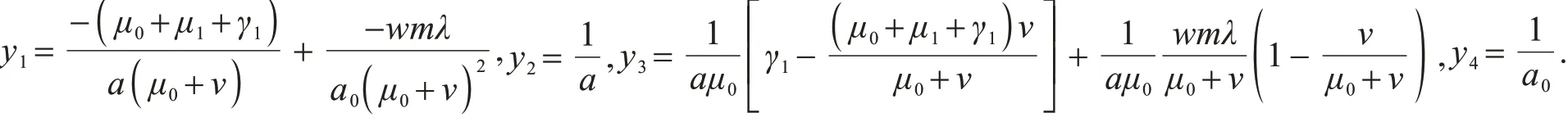
另外，左特征向量为z=(z1，z2，z3，z4)，其中，z1=0，z2=1，z3=0，z4=0.根据引理1可知，当R0=1时，可以利用a1，b1的值判别分支的方向.模型（4）中f=(f1，f2，f3，f4)在(x*，α*)上用于计算a1，b1的非零二阶偏导有根据引理1可得

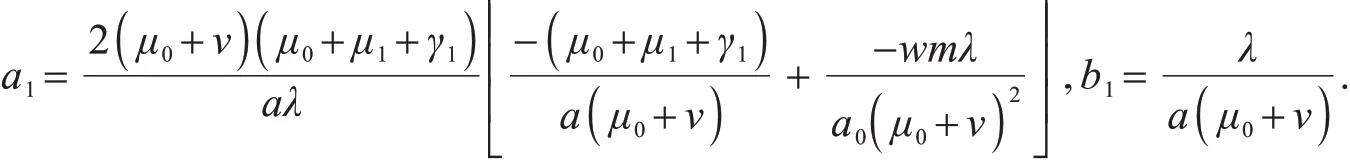
显然a1＜0，b1＞0.根据引理1，当R0=1时，模型（2）有一个前叉分支.

3.3平衡点的全局稳定性假设系统可以写成如下形式

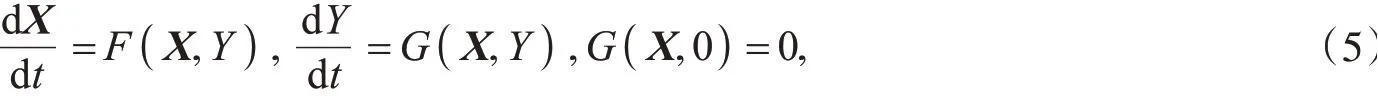
其中，X∈R3，Y∈R分别代表未感染者和感染者.设U0=(X0，0)为模型（5）的无病平衡点.

引理2［16］如果R0＜1，且满足下列2个条件：

2）对∀(X，Y)∈Γ，有其中DYG(X0，0)是一个M-矩阵，Γ是前文定义的变量边界，那么模型（5）的无病平衡点U0=(X0，0)是全局渐进稳定的.

定理3若R0＜1，则模型（2）中的无病平衡点E1是全局渐近稳定的.

证明根据引理2，把模型（2）改写，其中

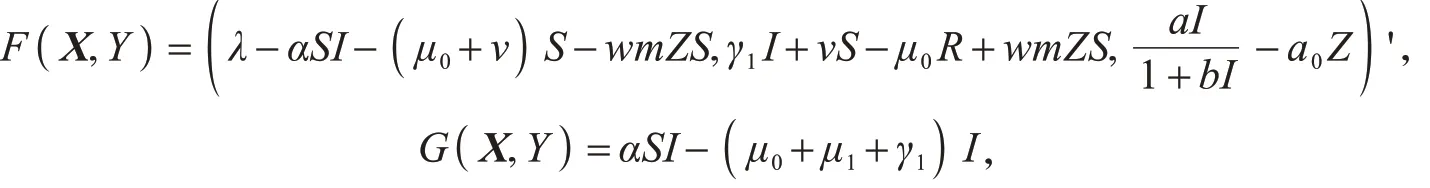
满足G(X，0)=0，X=(S，R，Z)＇，Y=I.

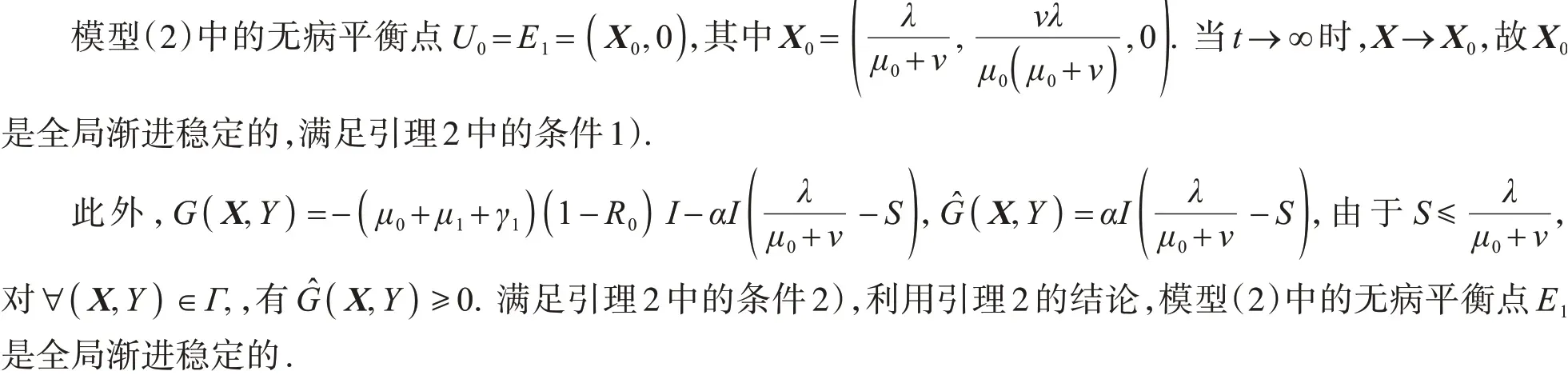
对于模型（2）中的疾病平衡点E2，可以构建一个Lyapunov函数来判别全局稳定性.

定理4当R0＞1时，模型（2）中的疾病平衡点E2是全局渐进稳定的.

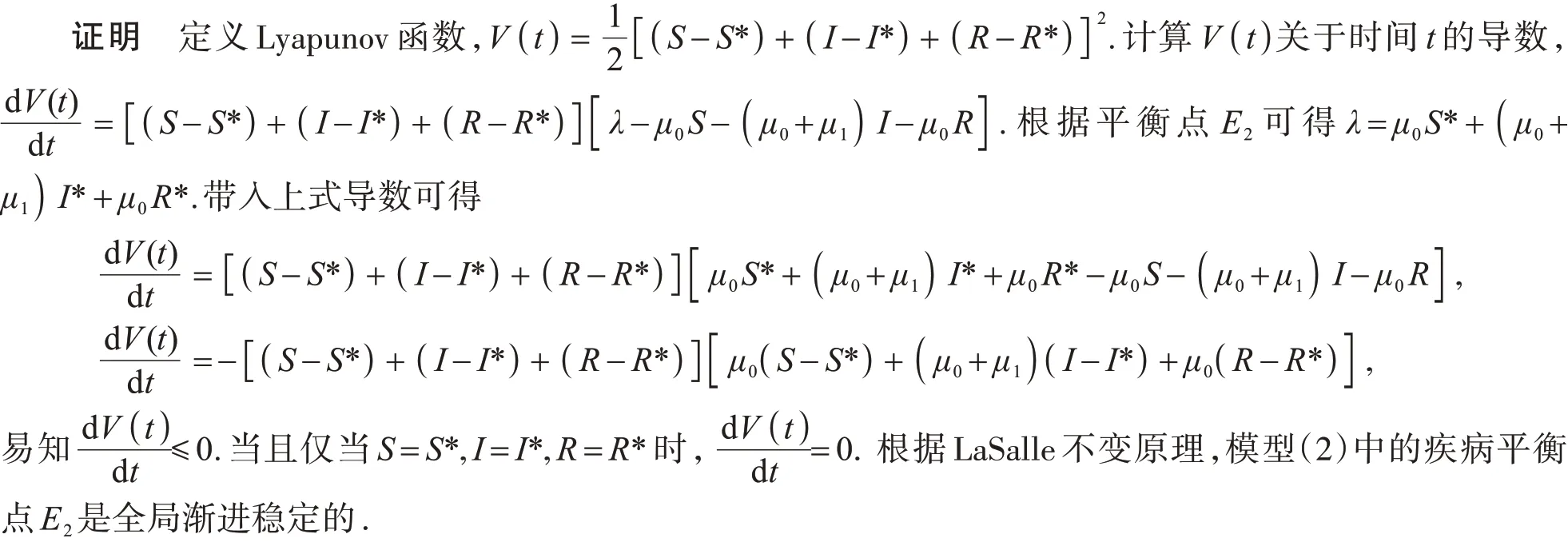
3.4局部敏感性分析模型（2）中的参数具有不确定性，会影响基本再生数R0的大小，局部敏感性分析揭示了基本再生数R0与模型中参数之间的关系.局部敏感性指标定义为［17］

其中，Π为模型中的参数.该分析提供了参数值与基本再生数之间的变化，为疾病的控制和传播提供了依据.利用式（6）和下列的参数值

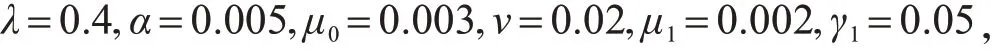
得到下列敏感度指标

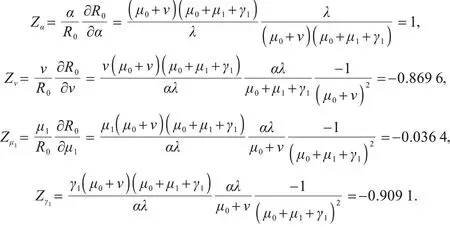
由上式可知，参数α与R0成正比，参数α的增加或减少都会使R0增加或者减少.另一方面，参数v，μ1，γ1与R0成反比，参数v，μ1，γ1的增加或减少都会使R0减少或者增加.因此，在局部敏感性分析的基础上，可以建立一个最优控制系统.

4 最优控制

为了探究如何有效控制HBV的传播，通过增加控制变量改进模型（2）.在模型（2）中添加3个控制变量：u1(t)表示疫苗的有效率，u2(t)表示信息反应强度大小，u3(t)表示对感染人群治疗的有效率.定义如下控制集

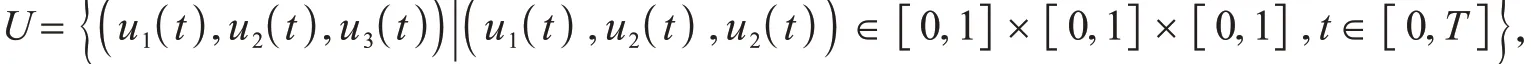
其中，T是控制策略结束的最终时间.方便起见，用u1，u2，u3表示3个控制变量.用k1I(t)表示感染人群的权重，k2，k3，k4分别表示疫苗的有效率，信息反应强度大小，治疗的有效率的权重，k2u12，k3u22，k4u32分别描述了疫苗接种，信息传播和治疗的相关成本.为了降低感染人群的数量，并使疫苗接种，信息传播和治疗成本最低.因此，控制问题可以描述为

受约束于

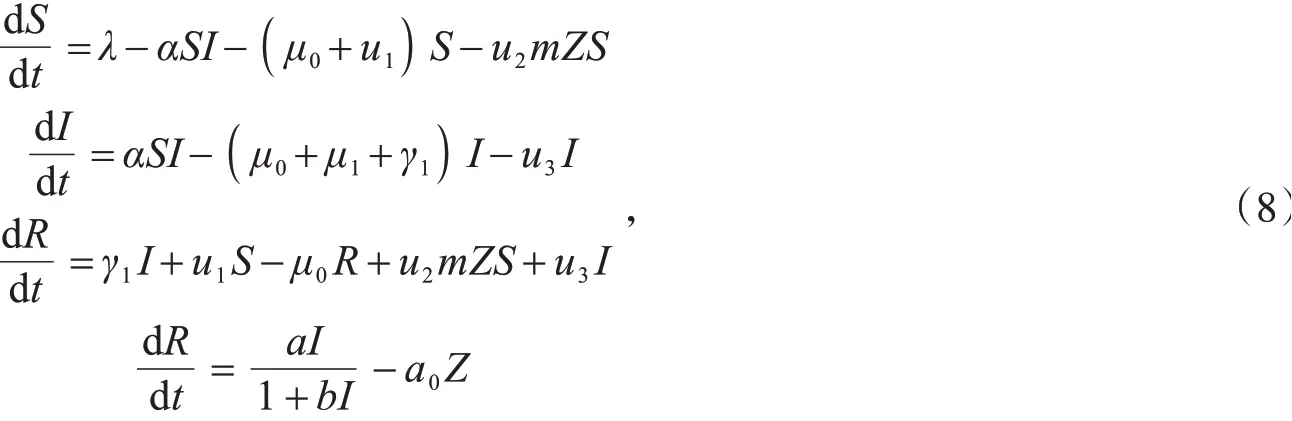
其中，k1，k2，k3，k4都是正常数.式（7）表示为了控制疾病传播的总代价，因此，寻找最优控制u*=(u1*，u2*，u3*)，即使得J(u*)=minJ(u1，u2，u3).

定理5对于最优控制问题（7）和（8），在U中一定存在最优控制u*=(u1*，u2*，u3*)，得J(u*)=minJ(u1，u2，u3).

证明为了证明最优控制的存在性，利用文献［18］中的方法.根据定义，控制集U是凸闭集.由于控制变量和状态变量都是非负的值，所以在最小值的问题上，目标函数（7）在u1，u2，u3中的必要凸性是满足的.因此，可以看出最优系统是有界的，确保了最优控制存在的紧密性.目标函数（7）中的被积函数在控制集U上是凸的.

证毕.

为了找到最优控制问题（7）和（8）的最优解，定义如下Hamilton函数

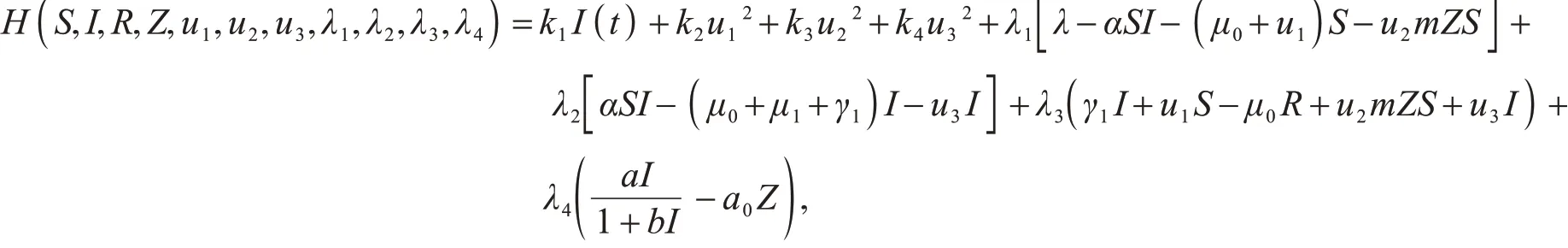
其中，λ1，λ2，λ3，λ4是协态变量，根据Pontryagin最大值原则，得到如下定理.

定理6如果u1*，u2*，u3*是最优控制问题（7）和（8）的最优控制变量，且S*，I*，R*，Z*是相应的最优状态变量，则存在协态变量λ1，λ2，λ3，λ4满足下列协态方程

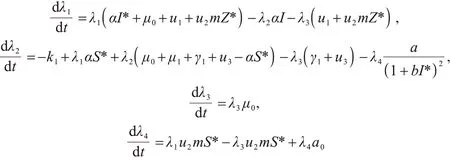
且边界条件为λ1(T)=0，λ2(T)=0，λ3(T)=0，λ4(T)=0.

此外相应的最优控制变量u1*，u2*，u3*为

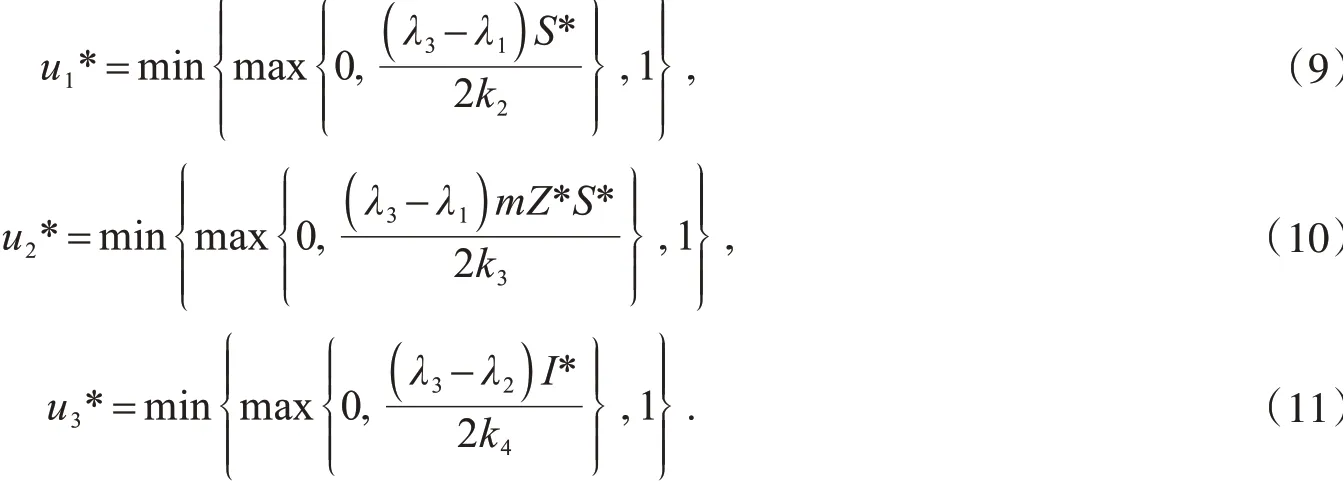
证明如果u1*，u2*，u3*是最优控制问题（7）和（8）的最优控制变量，且S*，I*，R*，Z*是相应的最优状态变量.根据Pontryagin最大值原则，那么存在协态变量λ1，λ2，λ3，λ4满足下列协态方程

根据定义的控制集U，有

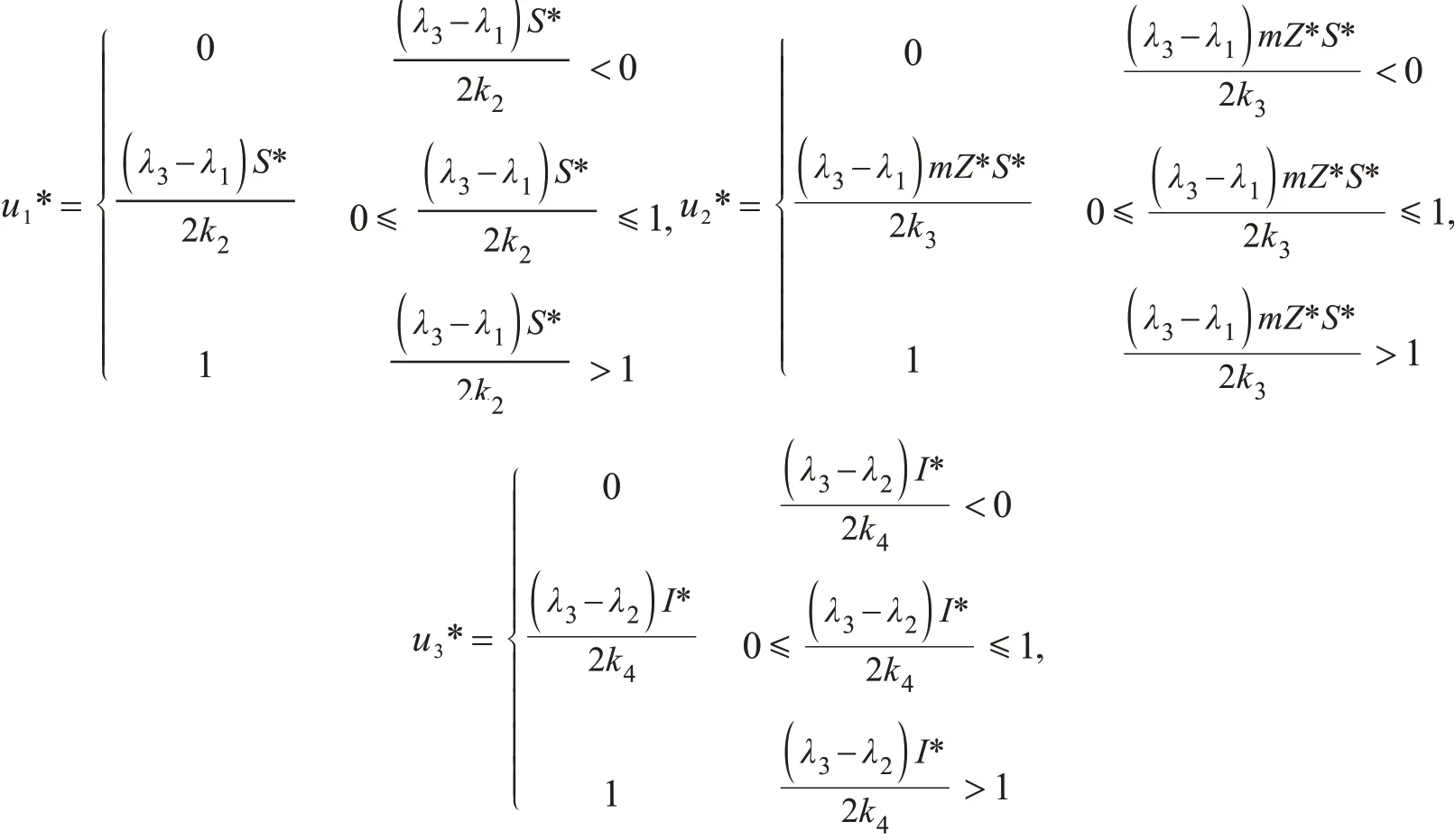
可以改写成式（9），（10）和（11）的形式.

证毕.

5 数值模拟

使用Runge-Kutta方法，参考Kumar［15］和Khan［18］等人的参数数据，利用Matlab软件进行数值模拟.

模型（2）给定初始值S(0)=100，I(0)=40，R(0)=20，Z(0)=10以及参数［15，18］：λ=0.4，α=0.005，μ0=0.03，μ1=0.002，γ1=0.05，v=0.02，m=0.017，w=0.2，a=0.01，b=1，a0=0.06，可以得到R0=0.487 8＜1，图2a验证了定理3.再使用同样的初始值以及参数［15，18］：λ=0.4，α=0.02，μ0=0.03，μ1=0.002，γ1=0.05，v=0.02，m=0.017，w=0.2，a=0.01，b=1，a0=0.06，可得R0=1.951 2＞1，图2b验证了定理4.

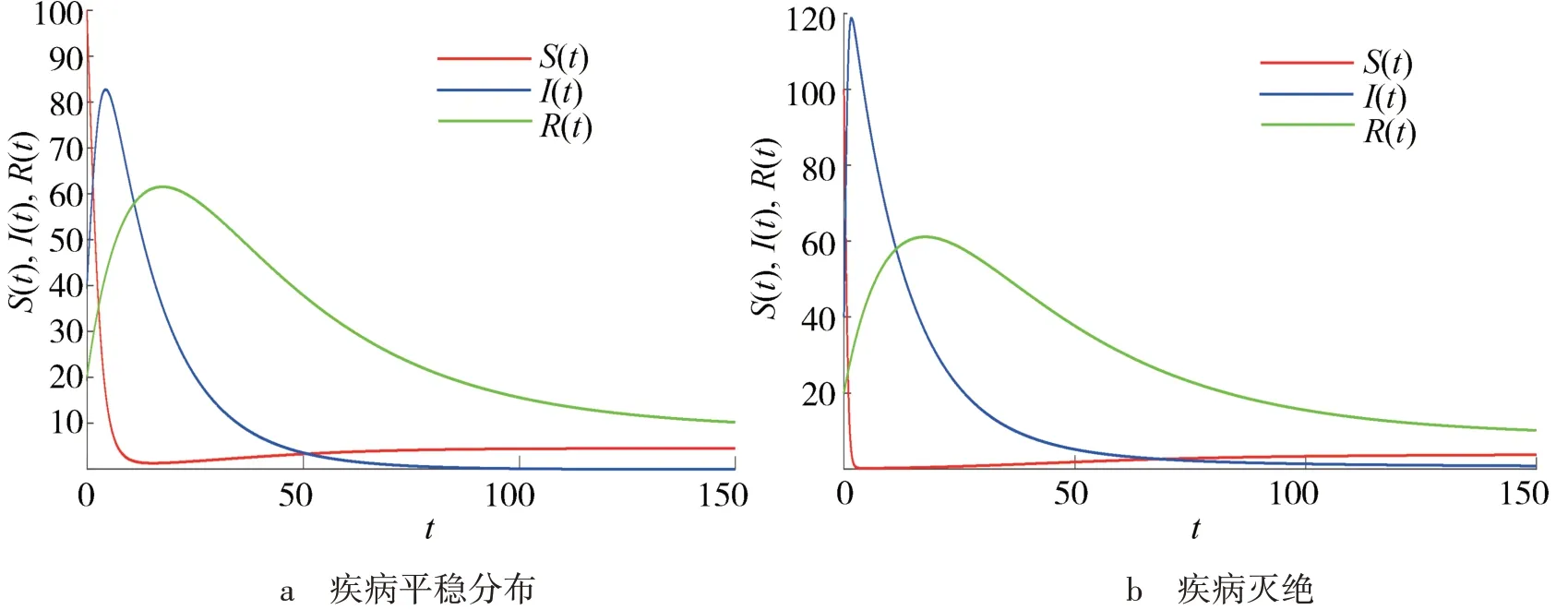
图2 模型（2）中疾病平稳和灭绝性分析

给定初始值S(0)=100，I(0)=20，R(0)=20，Z(0)=10以及下列的参数［15，18］：λ=0.4，α=0.005，μ0=0.03，μ1=0.002，γ1=0.05，v=0.02，m=0.017，w=0.2，a=0.01，b=1，a0=0.06，k1=1 000，k2=0.45，k3=0.55，k4=0.34.利用前推回代算法［15］解决控制问题（7）和（8），再对比没有施加控制时的ODE模型（2），易感人群，感染人群和恢复人群的数量对比分别表示在图3a，b和c中.

图3a结果表明，三维综合变量的引入，不仅大幅度地降低易感人群的数量，而且t=4为最低值，由于感染人群数量趋于零，疾病已经灭绝，不存在人与人之间的传播，所以易感人群不用再接种疫苗，又因为出生率大于死亡率，导致易感人群数量会慢慢增加.从图3b可以看到，感染人数在控制变量的干预下几乎完全改变了趋势，不仅避免了峰值的出现，而且t=4时感染人数降为零，即三维综合控制策略不仅能大幅度地降低感人数，避免峰值的出现，而且能有效的缩短病源的阻断时间.图3c则表明恢复人群将在短时间内达到峰值.

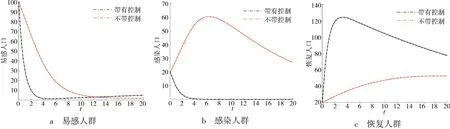
图3 α=0.005时控制对比图，

利用相同的方法，把接触传染概率系数提高6倍，即令α=0.03，初始值和其他参数都不变，同样对比

没有施加控制时的ODE模型（2），易感人群，感染人群，恢复人群的数量对比分别表示在图4a，b和c中.

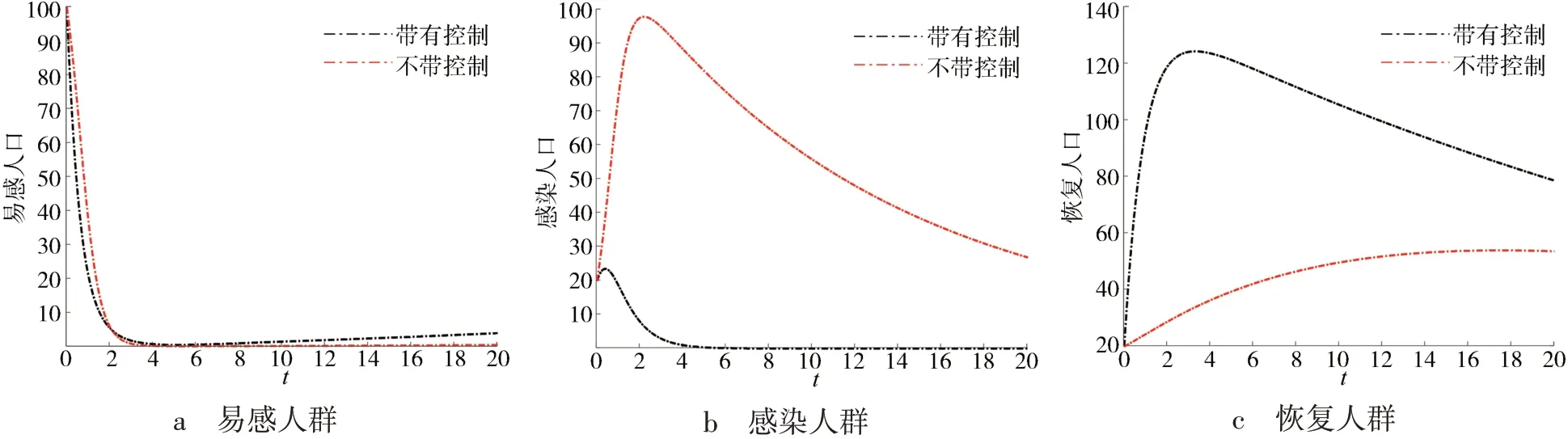
图4 α=0.03时控制对比图，

从图4可以看出，在扩大疾病传染概率的情况下，本文模型也能较好地降低易感人群的数量以及加快疾病的灭绝.

图5为最优控制问题（7）和（8）中最优控制变量的时间序列图.从图5中可以看出，在一开始时达到最大值，在一段时间后急速下降，最后下降到0，表明经过开始阶段的严厉措施后，随着时间的延长，控制强度可以慢慢降低趋于常态化，且u3*衰减最慢，即实际HBV传染源的阻断需要对感染人群的治疗投入较大，而疫苗有效率次之，信息反应强度最少.

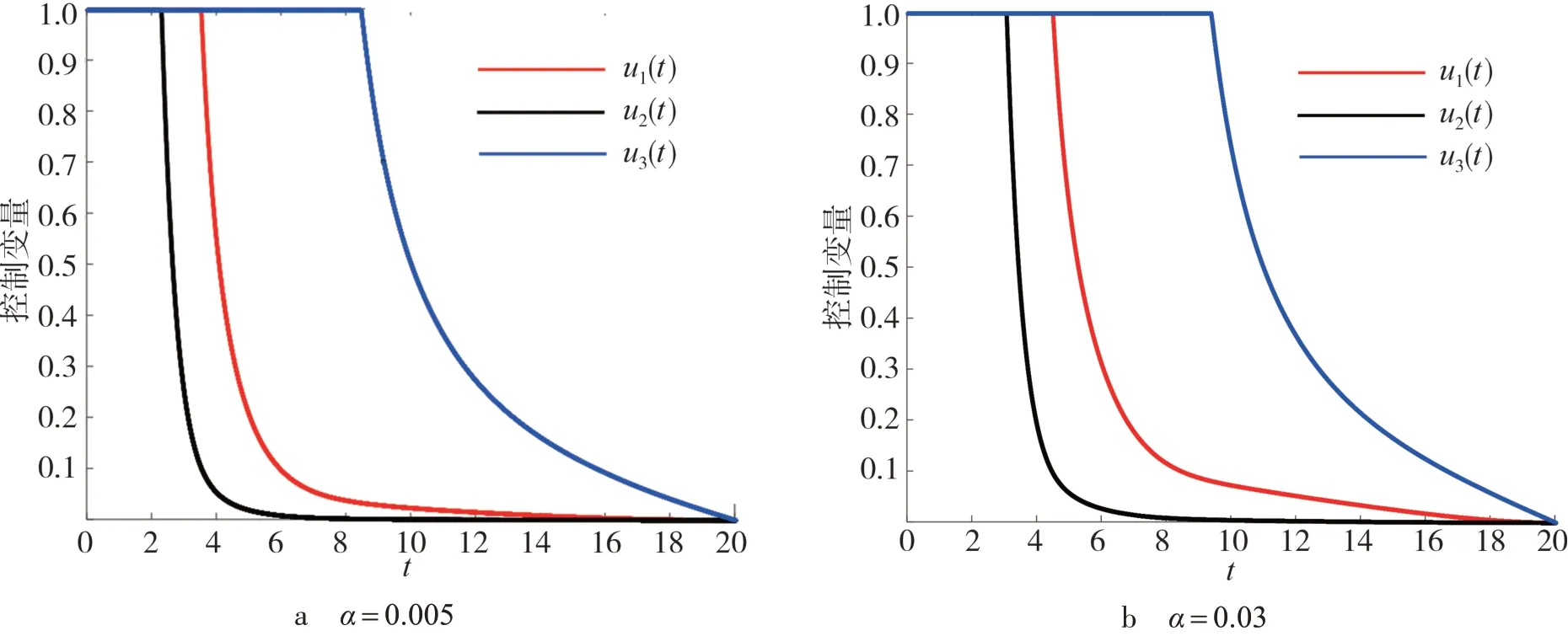
图5 最优控制变量时间序列图

6 小结

研究基于信息干预下HBV传染病模型，综合考察了信息干预、疫苗接种以及有效治疗率对模型动力学性质的影响.计算了新模型的基本再生数和模型的平衡点，根据线性化和构造Lyapunov函数的方法得到2个平衡点全局渐进稳定的条件.数值验证了2个平衡点的局部和全局渐进稳定性，并给出了其分支性质.通过参数敏感性分析，引入控制变量，探究最优控制问题（7）和（8），验证了最优控制的存在性并且根据Pontryagin最大值原则得出了最优控制变量的表达式.结果表明，加入控制后能加速疾病的灭绝，有效地控制了疾病的传播.