探究导数中的隐零点问题

黄 可

(江苏省南京市宁海中学高三(2)班,210024)

一、研究背景

函数是高中数学的重要研究对象,函数的零点问题,尤其是超越函数的零点问题成为函数压轴题的命题热点.有一种零点客观存在,但解不出来,我们通过研究它的取值范围、利用它满足的等量关系进行消元、换元、降次等方式能够达到解决问题的目的,这类问题就是隐零点问题.此类问题往往要借助零点存在性定理、函数的单调性,找到函数零点的有效位置,一般对零点设而不求,通过整体代换或消超越式进行化简,再结合其他条件来解决问题.

二、探究问题

1.利用零点定理进行估值

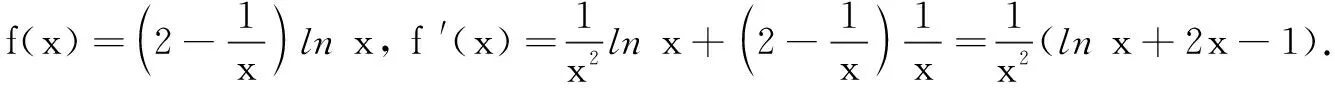
因为f(x)≥λ在(0,+∞)恒成立,且λ为整数,所以λ≤-1,即λ的最大值为-1.

反思本题在研究g(x)的零点时,需要通过零点存在定理来估值,找到隐零点所在的区间.需要注意的是这个区间不能太大,需要控制在尽量小的范围内,否则会影响最后得到的f(x0)的取值范围,导致结果不理想.

2.利用隐零点的性质求函数最值

例2已知函数f(x)=xex-ax+b的图象在x=0处的切线方程为y=-x+1.

(1)求a,b的值;

(2)当x>0 时,f(x)≥lnx-x+m,求实数m的取值范围.

解(1)a=2,b=1.(过程略)

(2)当x>0 时,f(x)=xex-2x+1≥lnx-x+m,即m≤xex-x-lnx+1.

综上,得m≤g(x)min=2,即m∈(-∞,2].

反思本题由g′(x0)=0 会得到隐零点满足的一个方程,该方程隐含了隐零点本身具有的性质,为后续在函数最值表达式中进行整体消元提供了便利,方便了函数最值的间接计算.此处的消元原则是尽量消超越式,这样会使函数的最值表达式变得比较简单,使问题达到转化与化归的目的.

3.利用隐零点的性质证明不等式

例3已知函数f(x)=ex-ln(x+m),当m≤2时,求证:f(x)>0.

证明当m≤2,x∈(-m,+∞) 时,ln(x+m)≤ln(x+2),故只需证明当m=2 时有f(x)>0.

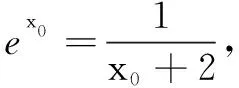
反思本题先由对数函数的单调性消去参数,利用必要条件简化证明途径;再由零点定理明确隐零点的取值范围,结合上述消元原则消去最小值f(x0)中的超越式,方便了函数最值的符号的判别.

三、方法整理

观察总结以上隐零点问题的求解过程,可以得到解决此类问题的一般策略:

第一步:用零点存在定理判断导函数零点的存在性,列出零点满足的方程,并结合函数的单调性得到隐零点的取值范围.当函数的隐零点不可求时,首先可用特殊值进行“投石问路”.特殊值的选取原则是:(1)在含有lnx的复合函数中,常令x=ek,尤其是令x=e0=1进行试探;(2)在含ex的复合函数中,常令x=lnk(k>0),尤其是令x=ln 1=0进行试探.

第二步:以零点为分界点,说明导函数符号的正负,进而得到题设函数最值的表达式.

第三步:将零点满足的方程适当变形,利用隐零点具有的性质整体代入函数最值表达式中进行化简,达到求函数最值、求参数取值范围、证明不等式、解不等式等目的,使问题获解.

(指导老师:居加颖)