高二数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分.在每小题给出的选项中,只有一项符合题目要求)

2.以F(0,1)为焦点的抛物线的标准方程是( )

(A)x2=4y(B)x2=2y

(C)y2=4x(D)y2=2x

3.两平行直线x+2y-1=0与2x+4y+3=0的距离为( )

4.在正项等比数列{an}中,a1=3,且3a2是a3和a4的等差中项,则a3=( )

(A)6 (B)27 (C)3 (D)12

7.函数f(x)的定义域是R,f(1)=2,对任意x∈R,f′(x)>2x,则不等式f(x)>x2+1的解集为( )

(A){x|x<-1或x>1}

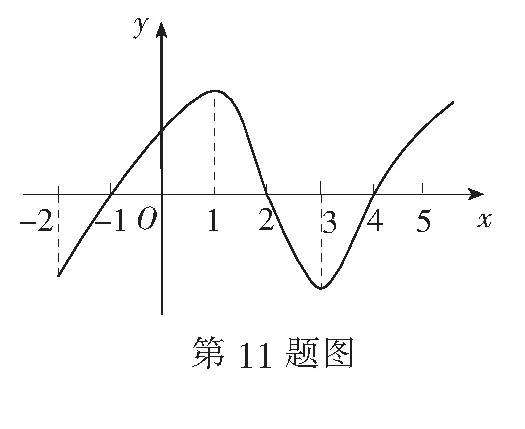
(B) {x|x<-1或0

(C) {x|x>1}

(D) {x|x<1}

8.从圆C1:x2+y2=16上的一点向圆C2:x2+y2=4引两条切线,连结两切点间的线段称为切点弦,则圆C2内不与任何切点弦相交的区域面积为( )

(A)π (B)2π (C)3π (D)4π

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

9.下列求导过程正确的是( )

10.已知公差为d的等差数列{an}中,前n项和为Sn,且a3+a7=18,a4a5=63,则( )

(A)d=2 (B)a4=9

(C)S6>63 (D)S8>63

11.如图是y=f(x)的导函数f′(x)的图象,对于下列四个判断,其中正确的判断是( )

(A)当x=-1时,f(x)取得极小值

(B)f(x)在[-2,1]上是增函数

(C)当x=2时,f(x)取得极大值

(D)f(x)在[-1,2]上是增函数,在[2,4]上是减函数

(A)|AF|+|BF|为6

(B)∆ABF的周长的取值范围是(6,12)

三、填空题(本大题共4小题,每小题5分,计20分)

13.以两点A(-4,-2)和B(4,4)为直径端点的圆的方程是______.

14.在数列{an}中,a1=4,且a1a2…an=(n+1)2,则an=______.

15.已知函数在f(x)=x3+3mx2+nx+m2(m,n∈R),x=-1时取得极小值0,则m+n=______.

四、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知等差数列{an}的前n项和为Sn,且a6=a4+4,S5=7a2.

(1)求数列{an}的通项公式;

(2)设bn=an+2an-1,求数列{bn}的前n项和Tn.

18.(本小题满分12分)已知圆C:(x-3)2+(y-4)2=4;

(2)若直线l过点B(1,0)与圆C相交于P,Q两点,求∆CPQ的面积的最大值.

19.(本小题满分12分)已知函数f(x)=x3-3x.

(1)求曲线y=f(x)在点(2,f(2))处的切线方程;

(2)求函数f(x)的单调区间和极值.

20.(本小题满分12分)已知等差数列{an}和等比数列{bn}满足a1=3,b2=9,an=3log3bn,n∈N*.

(1)求数列{an},{bn}的通项公式;

(2)设数列{an}中不在数列{bn}中的项按从小到大的顺序构成数列{cn},记数列{cn}的前n项和为Sn,求S30.

(1)求椭圆E的方程;

(2)若点P(5,0),记直线PA,PB的斜率分别为k1,k2,证明:k1+k2为定值.

22.(本小题满分12分)已知函数f(x)=ax+lnx+1.

(1)讨论f(x)的单调区间;

(2)对任意的x>0,不等式f(x)≤ex恒成立,求实数a的取值范围.

参考答案

一、单项选择题

1.B;2.A;3.B;4.D;5.C;

6.B;7.C;8.A.

二、多项选择题

9. BC;10.AD;11.ACD;12.ABD.

三、填空题

13.x2+(y-1)2=25;

四、解答题

17.(1)设{an}的公差为d,由已知条件得

解得a1=3,d=2.

所以数列{an}的通项公式为an=2n+1.

(2)由(1)得bn=an+2an-1=2n+1+22n=2n+1+4n.所以

18.(1)圆C的圆心C(3,4),半径R=2.

当直线l的斜率不存在时,直线l的方程:x=2,显然满足d=1.

当直线l的斜率存在时,设直线l的方程为y-3=k(x-2),即kx-y+3-2k=0.

综上,直线l的方程为x=2或y=3.

19.(1)f′(x)=3x2-3,所以f′(2)=9,f(2)=2,所求切线方程为9x-y-16=0.

(2)f′(x)=3x2-3.

令f′(x)>0,得x>1或x<-1;令f′(x)<0,得-1

所以f(x)的极小值为f(1)=-2,极大值为f(-1)=2.

20.(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.

由a1=3,b2=9,an=3log3bn,n∈N*,可得b1=3,a2=6,则d=3,q=3.

所以an=3n,bn=3n,n∈N*.

(2)当直线l斜率存在时,设其方程为x=my+1,令A(x1,y1),B(x2,y2).

当直线l垂直于y轴时,点A,B分别为椭圆E的左、右顶点,则k1=k2=0,有k1+k2=0.

综上，k1+k2为定值0.

所以在x=1处y=g(x)取得最小值g(1)=e-1.

由a≤e-1,得a的取值范围是(-∞,e-1).