一道全国高考题的多彩解法及背景挖掘
张艳宗
(浙江省海盐县元济高级中学,314300)
一、试题呈现
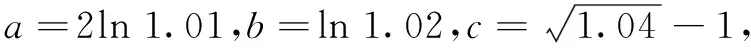
(A)a (C)b 这是2021年全国乙卷理科的第12题.此题通过对数与幂的大小比较考查对数函数、幂函数等基本函数,要求学生具有较高的数学运算素养,以及分析问题解决问题的能力.问题设置简洁,内涵丰富,是一道值得深究的好题.笔者对其进行了一番研究,给出此题几种解法,追根溯源,挖掘命题背景,分析其给高三数学复习教学带来的启示. a,b是同底的对数,可利用对数运算和对数函数的单调性转化为真数大小的比较.由a=2ln 1.01=ln(1+0.01)2=ln(1+0.02+0.012)>ln 1.02=b,得a>b. 思路1本题难点是比较a,b与c的大小.考虑到a与c(或b与c)的结构差异,将0.01看作变量x的一个值,构造函数,运用函数的单调性比较大小. 解法1构造函数法1 综上,b 思路2用单调性比较三个数的大小,计算量较大.可考虑利用函数的增减速度(即导函数的大小)定性判断,以减少计算量. 解法2构造函数法2 思路3比较对数a,b与c的大小,可考虑使用与对数函数y=lnx有关的函数不等式求解. 解法3函数不等式法 我们可以证明当x>1时,恒有 ① 即a>c. 即b 综上,选B. 不等式①来源于下面两个问题: 将以上两个问题整合,即为对数均值不等式 ② 知晓了①式的来历,我们也可直接利用对数均值不等式求解. 解法4对数均值不等式法 综上,选B. 这些公式被编入计算工具,计算足够多的项就可以确保显示值的精确性.比如用前三项计算cos 0.3,并与上述结果比较. 上述公式称之为泰勒公式,它是高等数学中的非常重要的一个内容,能将一些复杂的函数近似地表示为简单的多项式函数.泰勒公式这种化繁为简的功能,在近似计算、不等式证明等方面发挥着重要的作用. 解法5泰勒公式法 评注通过泰勒展开式,我们可以得到a,b,c较为精确的估值,明白设置1.01,1.02,1.04这些数据的原因.这可能是这道高考题的高等数学命题背景. 无独有偶,2014年新课标II卷理科第21题也是以此为背景的: 试题已知函数f(x)=ex-e-x-2x. (1)讨论函数f(x)的单调性; (2)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值; 近年来的高考题越来越注重基础知识与基本方法的融会贯通,需要学生用数学的眼光和数学思想分析问题、解决问题.在高三复习教学中,我们要注重引领学生夯实基础知识,展示问题的解题思路、数学思想方法,剖析思维过程,优化思维层次,构建良好的认知结构,强化学生分析问题、解决问题的能力. 在高三复习教学中,我们要挖掘教材中典型例题、习题和往年高考题的内涵与外延.不仅要求学生了解一些核心概念产生的背景和过程,理解问题所蕴含的知识、方法和思想,还要适当拓展一些难度适中的课外知识.这既可以扩展学生的视野,提高学生解决问题的能力,又可以加深学生对数学知识的理解与应用,提升数学素养.二、解法探究



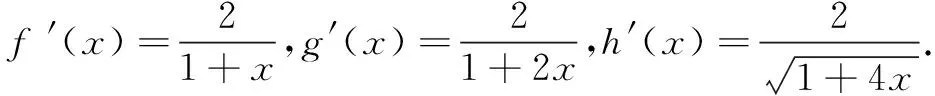
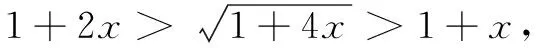

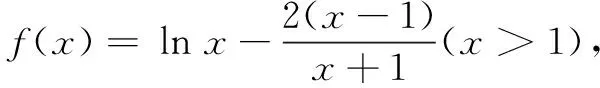


三、背景挖掘

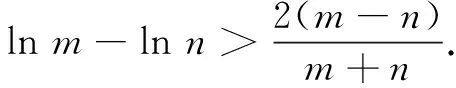


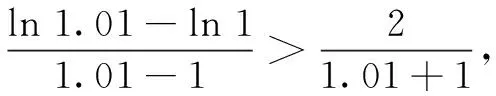


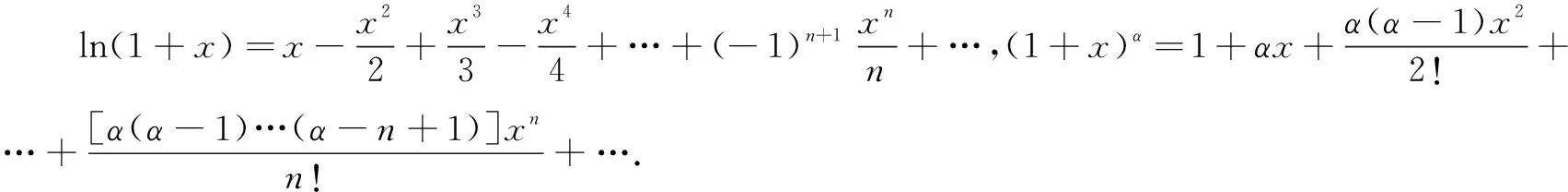
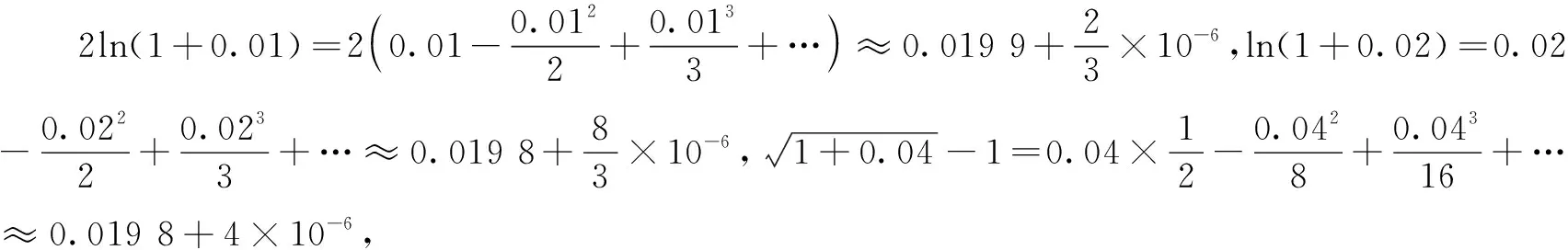

四、教学启示

