突破向量数量积难点的有效策略

孔志文 蒋晓东

(北京市朝阳外国语学校，100012) (北京市朝阳区教育科学院，100028)

向量是高中数学的重要内容之一,是连接代数与几何的桥梁,也是一种重要的数学工具.而向量的数量积是实数,是连接向量和实数的纽带.有关数量积的问题一般比较灵活,是学生思维发展的重要载体.数量积一般涉及模长、夹角、坐标等方面,是向量代数及几何特性的综合表现.在处理有关向量数量积问题时,一般可以从定义法、基底法和坐标法三个方面思考,综合运用转化与化归、数形结合、函数与方程等数学思想解决问题.下面以一道选择题为例阐述有关向量积问题解决的几种有效策略,望广大读者批评指正.

一、问题呈现

分析本题是一个数量积问题,表述简洁、结构新颖,难点在于如何根据条件合理转化不等式问题.探求本题的解决对于提高学生分析问题和解决问题的能力有着重要的意义.

二、策略探索

策略1定义法

运用数量积的定义,可将向量的数量积问题转化为投影问题,然后根据已经条件求相关线段的取值范围.

解法1如图1,由于∠BAC=90°,BC=2,以AB,AC为邻边作矩形ABDC,设其外接圆为⊙O.

由已知条件，可得

亦即点P只能在与AD垂直的弦EF上.

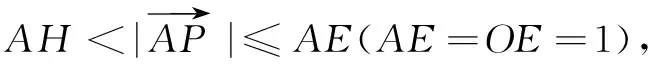
策略2坐标法

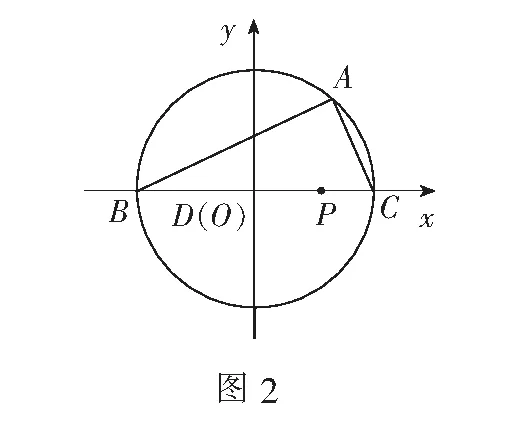
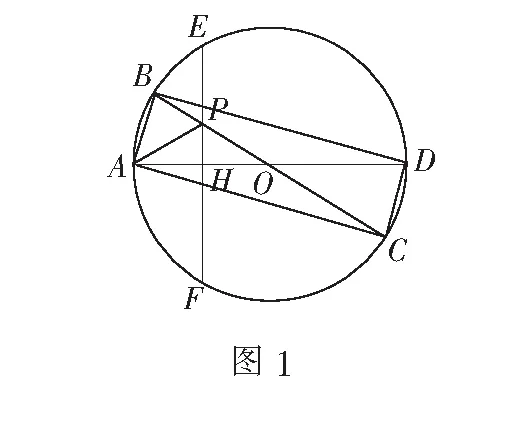
解法2以BC的中点D为坐标原点,BC所在直线为x轴,建立如图2的平面直角坐标系,则点B(-1,0),C(1,0).

设点P(t,0),A(x,y),易知-1≤t≤1.

由∠BAC=90°,BC=2,可知|AD|=1,即

x2+y2=1.

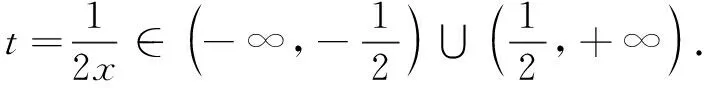
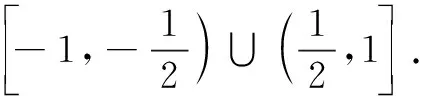
策略3基底法

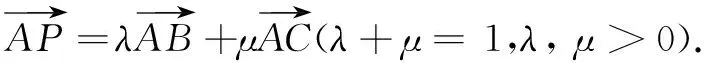
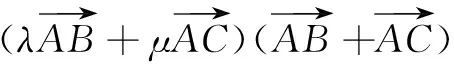
λa2+μb2=1.

a2+b2=4.

三、结束语

向量数量积相关问题的解决需要和函数、方程、不等式相关内容联系起来,有时候还需要和解析几何等内容联系起来,它是高中生进行研究性学习很好的载体.广大师生在教和学的过程中都要高度重视,对于学生思维的发展大有裨益.