分类例析参数法在竞赛题中的应用

路雪梅

(山东省东营市利津县高级中学，257400)

参数法是一种重要的数学解题方法.利用参数可以传递信息,沟通不同条件之间、条件与结论之间,乃至不同变量之间的紧密联系,达成数学不同模块的相互转换,优化解题过程.本文以圆与椭圆的参数方程为例,举例说明参数法在数学竞赛题中的应用,彰显参数在此处的两个应用价值:一是通过参数简明地表示曲线上任意一点的坐标;二是将曲线的有关计算问题转化为三角问题,从而运用三角函数性质及变换公式帮助我们求解诸如最值、参数取值范围等问题.

一、求函数的值域

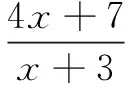
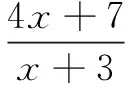
在圆x2+y2=r2的参数方程x=rcosθ,y=rsinθ(θ为参数,r>0)中，参数θ表示旋转角，这是其几何意义.一般地，圆(x-a)2+(y-b)2=r2的参数方程为x=a+rcosθ,y=b+rsinθ(θ为参数，r>0).

二、求参数的取值范围

(A)(-∞,-4] (B)[-4,+∞)

(C)(-∞,4] (D)[4,+∞)

评注本题将点P的坐标用椭圆的参数方程表示,代入不等式后分离出参数m,利用三角代换进行转化,避开了常规思路繁杂的运算,为简化最值的求解过程铺平了道路.

三、求最值

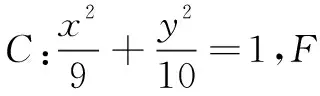
解易知点A(3,0),F(0,1).

评注本题将点P的坐标用椭圆的参数方程表示,将四边形分割为两个三角形后,面积表示为三角函数形式,利用辅助角法和正弦函数的有界性求得最值,充分体现了参数法解题的优越性.

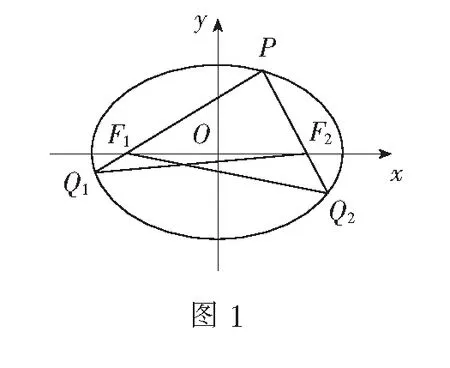
解易知焦点F1(-1,0),F2(1,0).设点P(x0,y0),Q1(x1,y1),Q2(x2,y2),由条件可知x0>0,y0>0,y1<0,y2<0.

以下先求y1-y2.

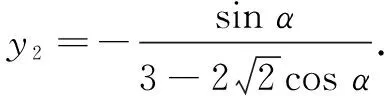
四、求动点的轨迹

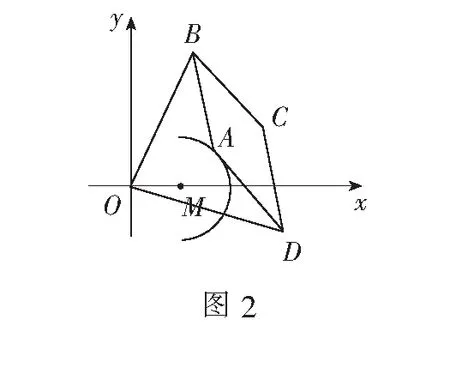
例5(2012年全国高中数学联赛题)如图2，在平面直角坐标系xOy中，菱形ABCD的边长为4，且|OB|=|OD|=6.

(1)证明：|OA||OC|为定值；

(2)当点A在半圆M：(x-2)2+y2=4(2≤x≤4)上运动时，求点C的轨迹.

解(1)定值为20.(过程略)