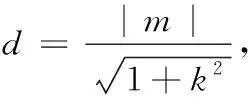高三数学综合测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

(A)3 (B)6 (C)9 (D)12

5.已知命题p:∀x∈R,ax2+ax+1>0,命题q:函数y=-(a+1)x是减函数.则命题p成立是q成立的( )

(A)充分不必要条件

(B)充要条件

(C)必要不充分条件

(D)既不充分也不必要条件

(A)3π (B)4π (C)9π (D)12π

(A)an=n(B)an=2n

(C)an=n+1 (D)an=n2-2n+3

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

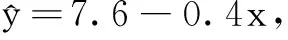
x681012 y6m32

(A)变量x,y之间呈正相关关系

(B)变量x,y之间呈负相关关系

(C)m的值等于5

(D)该回归直线必过点(9,4)

10.已知圆O的方程为x2+y2=1,过第一象限内的点P(a,b)作圆O的两条切线PA,PB,切点分别为A,B,下列结论中正确的有( )

(A)若点P在直线3x+4y-10=0上,则四边形OAPB的面积最小值为2

(B)四点O,A,P,B共圆

(C)直线AB的方程为ax+by-1=0

(A)π是f(x)的周期

(D)f(x)在[-202 1,202 1]中的零点个数不超过2 574个

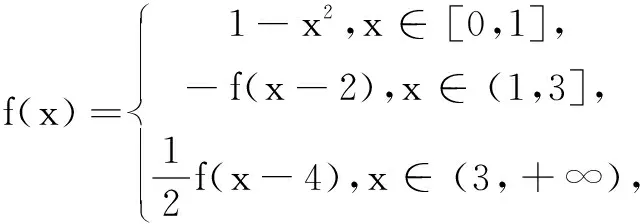
(A)f(x)是周期函数

(B)任意x1,x2∈R,|f(x1)-f(x2)|≤2

三、填空题(本大题共4小题,每小题5分,计20分)

15.已知非零向量a,b满足|b|=2|a|,且(a+b)⊥a,则a与b的夹角为______.

16.古希腊数学家阿波罗尼奥斯发现:平面上到两定点A,B距离之比为常数λ(λ>0且λ≠1)的点的轨迹是一个圆心在直线AB上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:

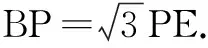
四、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知数列{an}的前n项和为Sn,且满足a1=2,Sn=2an-2,其中n≥2,n∈N*.

(1)求证:{an}是等比数列,并求{an}的前n项和Sn;

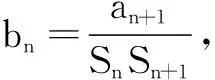
18.(本小题满分12分)已知∆ABC的三边a,b,c所对的角分别为A,B,C,若acosB+bcosA=2b,a=6,______.

(1)求角B;

(2)求边c.

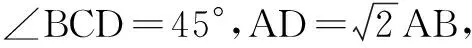
(1)证明:面PEF⊥面PAB;

(2)求面PEF与面PAD所成锐二面角的余弦值.

20.(本小题满分12分)2020年春,我国武汉出现新型冠状病毒,感染后会出现发热、咳嗽、气促和呼吸困难等症状,严重的可导致肺炎甚至危及生命.新型冠状病毒疫情牵动每一个中国人的心,为了遏制病毒的传播,危难时刻全国人民众志成城、共克时艰.某校为了了解学生对新型冠状病毒的防护认识,对该校学生开展网上防疫知识有奖竞赛活动,并从男生、女生中各随机抽取20人,统计答题成绩分别制成如下频率分布直方图和频数分布表:

女生成绩

规定:成绩在80分以上(含80分)的同学称为“防疫明星”.

(1)根据以上数据,完成以下2×2列联表,并判断是否有99%的把握认为“防疫明星”与性别有关;

男生女生合计 防疫明星 非防疫明星 合计

(2)以样本估计总体,以频率估计概率,现从该校男生中随机抽取4人,其中“防疫明星”的人数为X,求随机变量X的分布列与数学期望.

附:参考公式

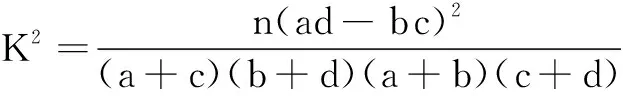
参考数据:

P(K2?k0)0.1000.0500.0250.0100.0050.001 k02.7063.8415.0246.6357.87910.828

21.(本小题满分12分)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

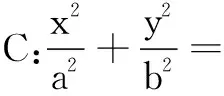
(1)求椭圆C的标准方程;

(2)O为坐标原点,若直线l与椭圆C交于M,N两点,直线OM的斜率为k1,直线ON的斜率为k2,当∆OMN的面积为定值1时,k1k2是否为定值?若是,求出k1k2的值;若不是,请说明理由.

参考答案

一、单项选择题

1.B; 2.C; 3.B; 4.B; 5.D;

6.C; 7.B; 8.C.

二、多项选择题

9.BCD;10.BCD;11. AD;12.BCD.

三、填空题

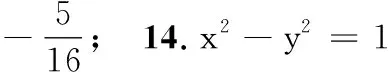
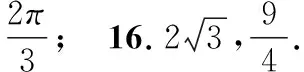
四、解答题

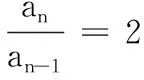
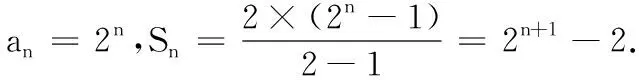
18.(1)由条件及正弦定理，可得sinAcosB+sinBcosA=2sinB,即sinC=2sinB,即c=2b.

取AD中点M,连结EM,因为ABCD是平行四边形,所以EM⊥BD.又因为EF∥BD,所以EM⊥EF.

因为∆PBC是等边三角形,E为BC中点,所以PE⊥BC.又因为平面PBC⊥面ABCD,平面PBC∩面ABCD=BC,所以PE⊥平面ABCD.

又因为EM，EF⊂平面ABCD,所以PE⊥EM，PE⊥EF.于是EM，EF，EP两两垂直.

平面PEF的法向量为n=(1,0,0),由m·n=0,得平面PEF⊥平面PAB.

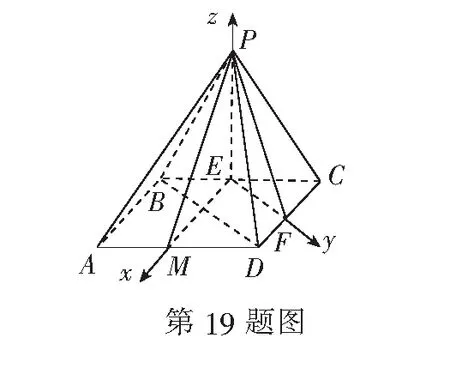
所以，平面PEF与平面PAD所成锐二面角的余弦值为

20.(1)由频率分布直方图，可得男生中成绩大于等于80的频率为(0.035+0.025)×10=0.6,故男生中“防疫明星”的人数为20×0.6=12人,“非防疫明星”人数为8人.

由频数分布表，可得女生中“防疫明星”的人数为6人,“非防疫明星”人数为14人.所以2×2列联表为

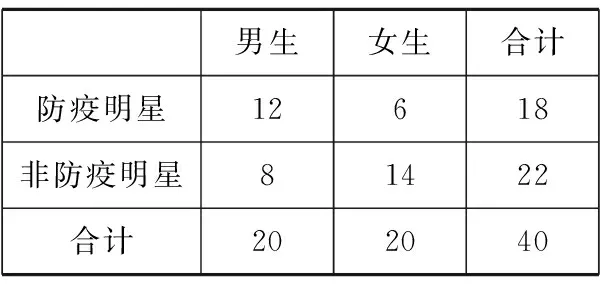
男生女生合计 防疫明星12618 非防疫明星81422 合计202040

X的可能取值为0,1,2,3,4.

所以随机变量X的分布列为

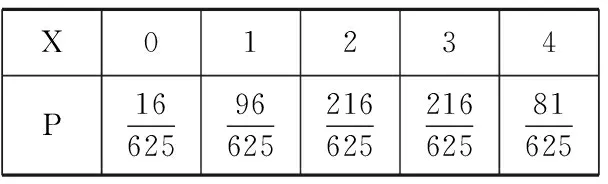
X01234 P166259662521662521662581625

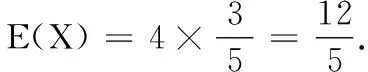
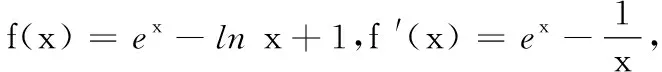
(2)由f(x)≥1,可得aex-1-lnx+lna≥1,即ex-1+ln a-lnx+lna≥1,即ex-1+ln a+lna+x-1≥lnx+x=eln x+lnx.

令g(t)=et+t,则g′(t)=et+1>0,g(t)在R上单调递增.由g(lna+x-1)≥g(lnx)，得lna+x-1≥lnx,即lna≥lnx-x+1.

由lna≥h(x)，得lna≥0,a≥1.故a的范围为[1,+∞).

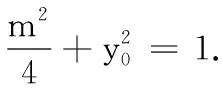
当直线MN的斜率存在时,设直线MN的方程为y=kx+m,点M(x1,y1),N(x2,y2).

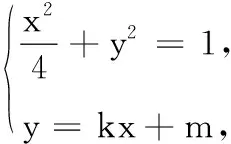
(4k2+1)x2+8kmx+4m2-4=0,

且Δ=64k2-16m2+16>0.