2021新课标Ⅰ卷第19题的解法探究
2022-04-11 10:15:00安徽省合肥一六八中学230601吴志勇王中学
中学数学研究(江西) 2022年4期
安徽省合肥一六八中学 (230601) 吴志勇 王中学
2021年高考新课标Ⅰ卷第19题是一道解三角形问题,主要考查了利用正余弦定理处理三角形中的边角关系,也考查了分析问题、解决问题以及运算求解能力等数学素养,体现了朴实中重视基础,常规中考查能力,为引领在新课程、新教材下开展高中数学教学起到了良好的导向作用.本文就此题的解法开展研究.
一、试题呈现
原题记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BDsin∠ABC=asinC.
(1)证明:BD=b;
(2)若AD=2DC,求cos∠ABC.
二、解法探究
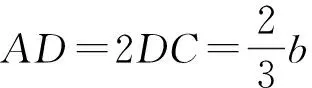
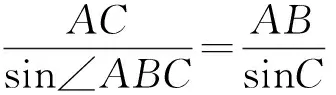
(法2)在△ABC中,由b2=ac得b·sin∠ABC=a·sinC,又BD·sin∠ABC=a·sinC,
∴b·sin∠ABC=BD·sin∠ABC.∵sin∠ABC≠0,∴BD=b.
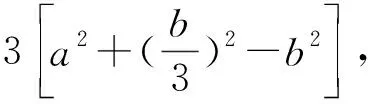
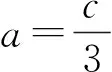
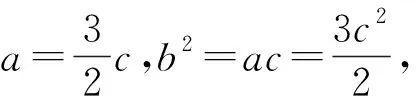
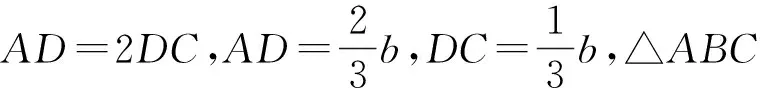
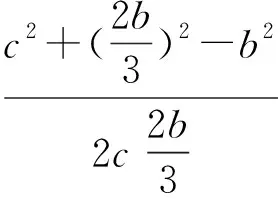
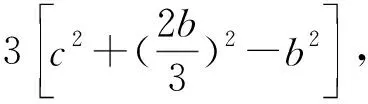
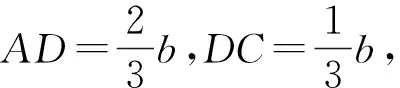
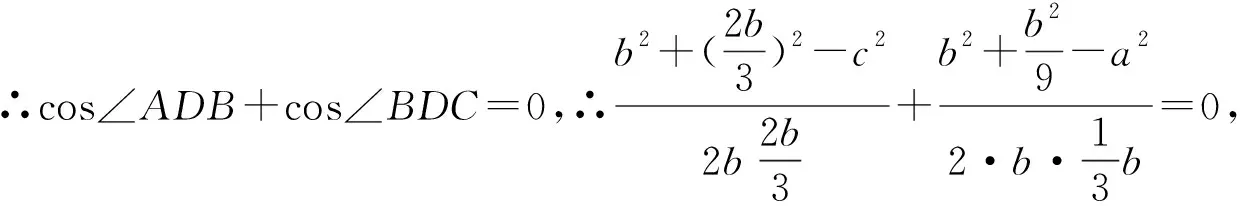
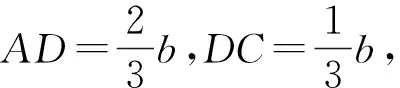
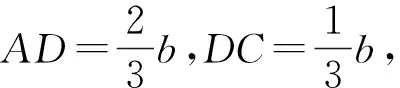
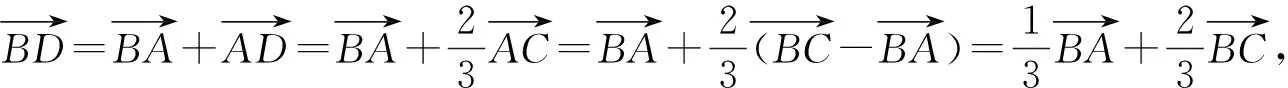
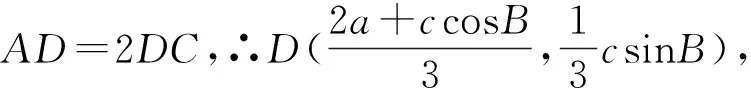
评注:解法1是利用△ABC与△ABD中∠A的余弦值相同,解法2是利用△ABC与△BCD中∠C的余弦值相同,解法3是利用△ABD与△BCD中∠ADB和∠BDC互补,余弦值的和为0,三种方法本质相似,借助角之间的关系以及已知条件b2=ac和AD=2DC来找出边a,b,c之间的等量关系,对学生的运算能力要求较高;解法4通过对已知条件BD·sin∠ABC=a·sinC的推理,找到∠ABC与∠BDC互补,继续可以利用余弦定理找出边之间的关系,而解法5则是利用了三角形相似得到了边之间的关系,方法巧妙,对学生的逻辑推理能力要求较高;解法6和7根源是余弦定理,但是分别利用了向量法和坐标法,一个是正余弦定理的推导工具,一个是三角函数概念的应用,方法不难,容易被忽略.本题充分体现了选拔功能,要求不同的学生选择不同的方法解决问题.
三、命题推广
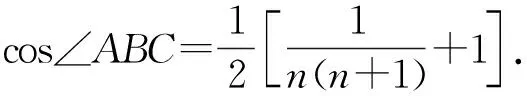
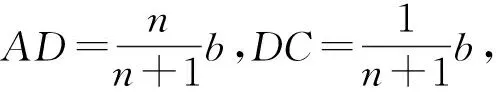
猜你喜欢
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
文理导航·科普童话(2017年7期)2018-02-10 19:42:29
小天使·四年级语数英综合(2017年6期)2017-06-07 10:45:55
智富时代(2017年4期)2017-04-27 02:13:48
小天使·二年级语数英综合(2017年3期)2017-04-01 20:49:17
中学数学杂志(高中版)(2016年6期)2017-03-01 18:53:58
小学生导刊(低年级)(2016年6期)2016-07-02 22:16:01
北京信息科技大学学报(自然科学版)(2016年5期)2016-02-27 06:31:40

