拓展解题思路，优化运算步骤*——以解析几何试题的求解为例

四川电影电视学院实验中学 (611331) 王昌林 罗萍双

解析几何试题的运算要求较高，如何简化解析几何中运算的策略很有意义.简化运算的方法有很多，如定义法、数形结合法、巧设未知数，几何分析，运用结论，特殊化等.本文予以论及.

1 运用定义，回归本质

俗话说：“万变不离其宗”.其意为尽管形式上变化多端，其本质或目的不变，殊途同归.如何抓住本质呢？最好的办法就是回归定义.利用定义解题，可以有效缩短解题过程，优化思维品质.

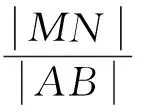
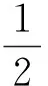
评注：由抛物线的定义将|MN|用|AF|，|BF|表示出来，从而解决问题.

2 数形结合，体现素养

伴随着新课程标准的推行，在高考试题中出现了越来越多需要用数形结合思想解决的题型.数与形有效结合的方法能够提升学生数学思维能力，帮助学生分析题意找到解题思路，达到高效的解题成果.

图1

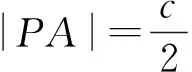
评注：圆锥曲线离心率的求解，半径和直径的判断，采用数形结合可以有效避免代数法从头至尾运算繁琐，提升准确率.

3 巧设方程，规避讨论

在解答解析几何试题时，合理的巧设方程可以有效的避免讨论.例如在解答直线与圆锥曲线的有关问题，可以将直线方程设为x=my+n，从而有效避免讨论直线的斜率.此外，还有妙用极坐标、参数方程等方式简化解析几何运算.

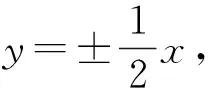
例4 设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1,0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD与点E.

(1)证明|EA|+|EB|为定值，并写出点E的轨迹方程；

(2)设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围.

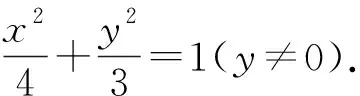
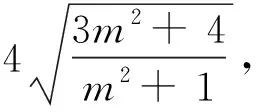
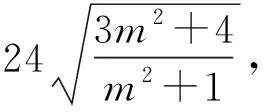
评注：例3与例4分别巧设双曲线与直线的方程，有效规避双曲线两种标准方程与直线斜率的存在性，优化解题目的，使得解题更加高效.

4 巧借未知，设而不求

“设而不求”是指增设辅助元却在解题过程中不求出所增设元值的一种方法.采用“设而不求”的方法，往往可以避免因盲目计算而造成的大量繁琐工作，从而达到简洁、快速的解题效果.

例5 已知抛物线C：x2=-2py经过点(2,-1).

(1)求抛物线C的方程以及准线方程；

(2)设O为原点，过抛物线C的焦点作斜率不为0的直线l，交抛物线C于M，N两点，直线y=-1分别交直线OM，ON于点A和点B，求证：以AB为直径的圆过y轴上的两个定点.

解析：(1)易得抛物线C的方程为x2=4y，准线方程为y=-1.

评注：先设出参数x1，x2，y1，y2，用参数表示直线OM的斜率，从而表示A，B两点的坐标.在表示圆的方程时发现方程中出现两根之积，于是联立方程并根据韦达定理得到x1x2=-4，从而解得y值，最终证明以AB为直径的圆过y轴上两个定点.

5 模型结论，减少运算

模型结论是指合理运用数学模型与重要结论解题的策略，其可以大大简化运算，尤其在选填题中效果明显.

例6 已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，则|AB|+|DE|的最小值为( ).

A.16 B.14 C.12 D.10

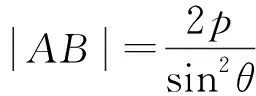
例7 已知点M(-1,1)和抛物线C：y2=4x，过C的焦点且斜率为k的直线与C交于A，B两点.若∠AMB=90°，则k=.

解析：已知点M(-1,1)在抛物线的准线上，且∠AMB=90°，则可知直线AB是切点弦方程，所以可得y=2x-2，则k=2.

评注：例6的抛物线焦点弦长公式以及例7的切线模型都是高考常考的问题，因此，掌握一些结论与模型是必要的，但模型和结论不可死记硬背或是对其痴迷，其应是在自己原有知识基础和直觉感知之上的.

6 等价转化，简化运算

等价转化是指将未知解法问题转化到已有知识的一个过程.解决综合试题时，根据题中给出的条件进行“精准”转化，使其能够计算且便于计算，甚至简算或者不用计算.

例8 已知抛物线C：y2=2x的焦点为F，平行于x轴的两条直线l1，l2分别交C于A，B点，交C的线段AB上，R是PQ的中点，证明：AR∥FQ.

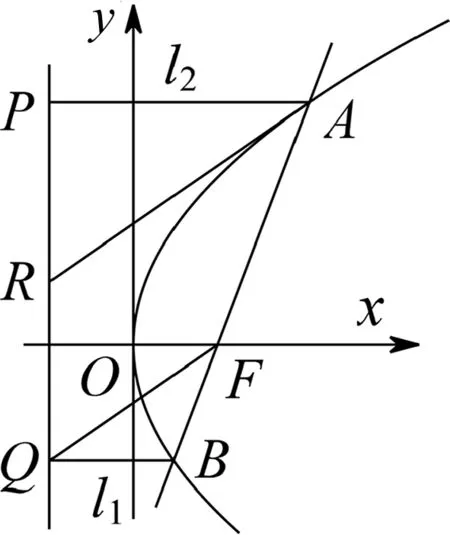
图2

评注：将两直线平行转化为直线斜率相等的方法是常见转换方式.大部分解析几何试题难在运算，而优化运算的根本在于转化.此外，转化的过程还会用到向量、导函数、不等式等工具.

7 巧借平几，几何分析

巧借平几是指借助与平面几何相关知识对解析几何问题进行求解.在解答解析几何问题时，进行适当的几何分析，注重挖掘问题的几何特征，善于用几何的眼光来审视问题，往往可以得到较为简洁的方法.

评注：本题若直接用坐标法建立等式，其运算量较大；现巧妙利用平面几何知识，不但能减少运算量，还能给人耳目一新之感.

8 发掘隐含，优化运算

“隐含条件”是指数学问题中没有明确指出的非显性条件.在解题时，应仔细审题，认真观察，充分挖掘并利用隐含条件，从而达到优化解题过程、多想少算等目的.

例10 已知椭圆C：9x2+y2=m2(m>0)，直线l不过原点O且不平行与坐标轴，l与C有两个交点A、B，线段AB的中点为M.

(1)证明：直线OM的斜率与l的斜率的乘积为定值；

解析：(1)kOM·kl=-9，过程略.

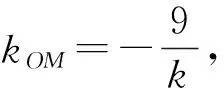
评注：运算能力的核心在于设计合理运算路径，若是采用设直线方程与椭圆联立的常规解题思路，会使得运算量大大增加以致无法操作.充分发掘P点横坐标是对角线的两倍这一“隐含条件”，运算量会大大减少.

9 高观导向，谋定而动

高观导向是指运用高等数学相关知识对解析几何试题的结果进行预判.高考中，高等数学知识虽不能直接使用，但可以帮助考生把握解析几何答案的预见性，从而做到对试题整体把控.

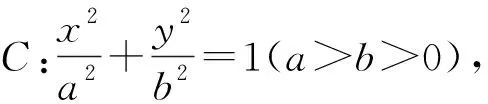
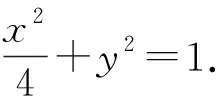
评注：例11与例12分别运用的是极点极线与二次曲线系方程的知识.例题若是采用一般方法解答，其过程是繁琐的，用高观进行导向，可以让考生在解答过程中及时更正.

10 直观想象，问题特殊化

运用特殊化策略是解答选择填空题的常用方法.从特殊到一般是人们思考问题的根本方法，也是探求解题思路的基本策略[5].在解答题中特殊化思想可以起到有效的导向作用，为寻找问题的突破口指明方向.

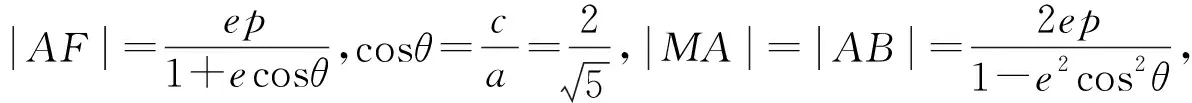
评注：考虑B，M重合，将问题特殊化，避免了联立、消元、韦达定理等一系列运算过程，达到简化运算地目的.

数学解题不仅要会算，更要会看、会想.以上示例更能有效解决解几何问题求解中“想到算不出”、“想想还会，算算就错”等问题.