一道结构不良试题的解法探究

重庆市铜梁二中 (402560) 李 波

1 试题呈现与条件分析

(2021年11月绵阳一诊理科题)在锐角△ABC中，角A,B,C所对的边分别为a,b,c，c=3，从以下三个条件中任选一个：①btanC=(2a-b)tanB；②2ccosB=2a-b；③accosA+a2(cosC-1)=b2-c2，解答如下问题.

(2)若AB边上的点P满足AP=2PB，求线段CP的长度的最大值.

在结构不良问题中，备选条件是从已有条件通向需解决问题的一座桥梁，因此，有必要先弄清楚备选条件究竟为问题的解决提供了什么条件或工具.下面逐个分析各备选条件.

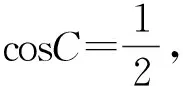
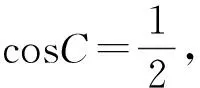
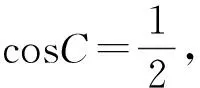
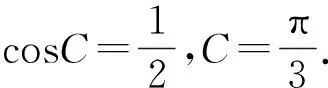
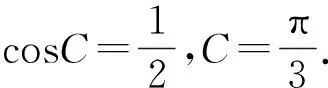
根据等式的结构，合理利用正弦定理或余弦定理实现边角互化使问题迎刃而解.一般而言，等式中仅出现余弦与边时，可采用余弦定理把余弦用边表示；等式中的边是齐次式时，可考虑用正弦定理把边用角表示.同时，也要注意三角恒等变换，三角形固有的性质(三角形内角和为180°，三角形的射影定理等)的灵活使用.

2 解法探究

2.1 第(1)问的解答

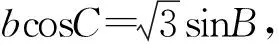
2.2 第(2)问的解答

由于AP=2PB，AB=3，则PB=1.

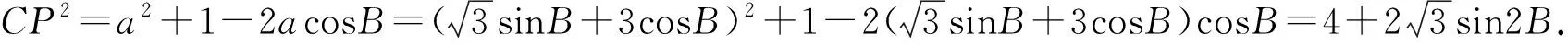
评注：运用第(1)问的结果，将CP2转化成三角函数的最值问题求解.此解法中，第(2)问作为第(1)问的自然延续，符合问题串式的命题原则.

评注：由余弦定理得到CP2的关系式，结合这些等式将CP2用三角函数表示，其中用到的积化和差公式可能是学生比较生疏的知识点.

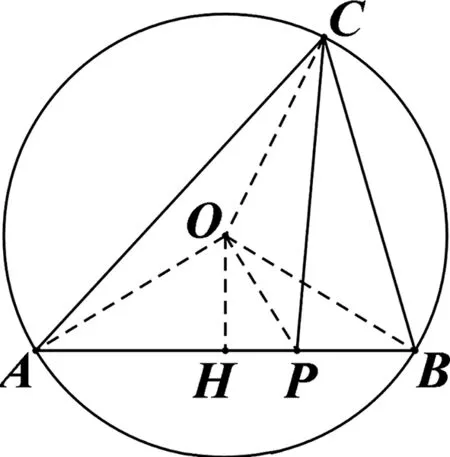
图1

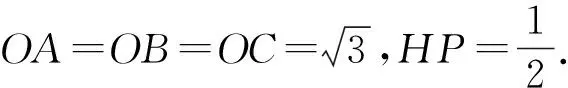
评注：由于角C及其对边c固定，联想到外接圆模型，并巧妙地把所求线段放到三角形中构造不等式求解.最后用余弦定理验证：当P,O,C共线时，△ABC为锐角三角形.这是有必要的.

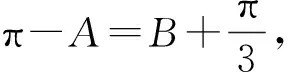
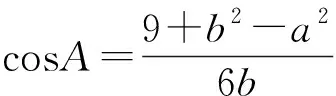
3 结语

广义的结构不良问题是现代认知心理学研究的内容.数学中的结构不良问题往往是指问题的起点和目标明确，提供若干解决问题的途径且预先不知道那种最优，但都能达到目标的一类题型，是近几年高考中出现频率较高的一种题型.这种结构不良问题有利于展现数学的趣味性，体会数学知识的应用价值，启迪数学智慧，提高数学核心素养，这与高中数学课程的基本理念不谋而合.另一方面，对同一个问题变换不同的视角寻求不同的解决方案，可以开拓思维视野，提升思维品质，将相关知识融合在一起，有利于学生从整体上把握并运用数学知识，这也是数学核心素养的基本要求.