对一道2021年全国高考题的深度研究*

扬州大学数学科学学院 (225002) 田雨童

历年高考中解析几何试题都被学生视为“难题”，解答解析几何问题的难点在于难切入，计算量大，那么如何简化解析几何问题，是值得研究的问题，本文就2021年全国乙卷的一道解析几何题，从多角度对其解法做出分析.

一、试题再现

本题的关键在于如何表示|PB|，结合已知条件|PB|≤2b得到答案，考查推理论证能力、运算求解能力，考查函数与方程的思想以及分类讨论的思想，考查数学运算、逻辑推理等核心素养，体现了基础性和综合性.

二、解法探究

思路1看作两点之间的距离

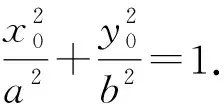
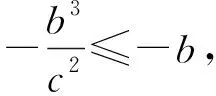
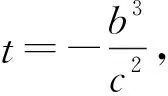
评注：解法1和解法2都是通过假设P点坐标，得到|PB|，即两点之间的距离，从而得到二次不等式，将恒成立问题转化为二次函数最值问题，降低了运算难度.

思路2看作过定点的直线与椭圆相交

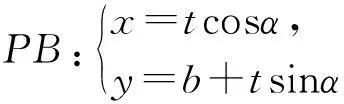
思路3将B看作极点，借助极径的几何意义

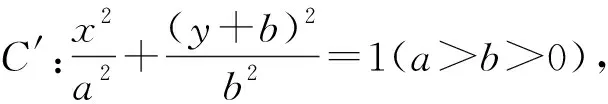
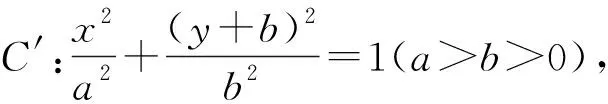
思路4看作两个曲线的位置关系

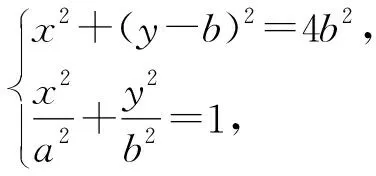
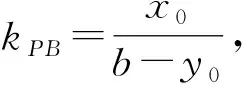
当x0=0时，P(0,-b)，经过验证符合题意；

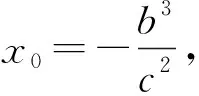
评注：解法5和解法6是将代数问题转化为几何问题，解法5将问题转化为椭圆C在圆M内，利用方程思想△=0，研究相切位置情况即可.而解法6是分别求出两曲线的切线，使其斜率相等作为求解桥梁，最后得到结果.

思路5从选项出发，得出结果

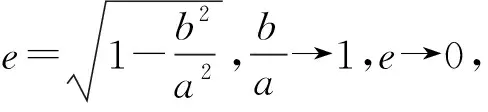
三、教学启示

通过以上的几种解法的分析，不难看出解答解析几何问题的关键在于如何确定算理，优化设法，简化计算.日常教学中，教师要引导学生从多角度去思考问题，不能仅仅停留在得出正确答案，要深入的理解一个题所考查的知识点，达到“以一当十”的效果，通过一题多解、多题一解的方法提高教学效率，让学生真正领会其中渗透的数学思想方法，领悟数学本质.