一道竞赛试题的多解及推广
2022-04-11 10:15:26福建省福清第一中学350300叶诚理福建省福清第三中学350315
中学数学研究(江西) 2022年4期
福建省福清第一中学 (350300) 叶诚理福建省福清第三中学 (350315) 何 灯
1.试题赏析
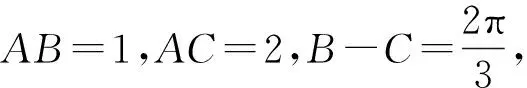

2.试题解析

评注:本解法通过正弦定理把边b,c的关系转化成角度B,C的关系,结合三角形内角和关系,运用三角恒等变换公式,转化成与角C相关的三角函数计算问题.

评注:本解法仍然是通过正弦定理把边的关系转化成角的关系,与解法一不同之处在于通过联立角A,B,C的关系,把角B,C统一用角A表示,从而得到关于角A的三角关系式,体现了消元、方程思想在解三角形中的应用.
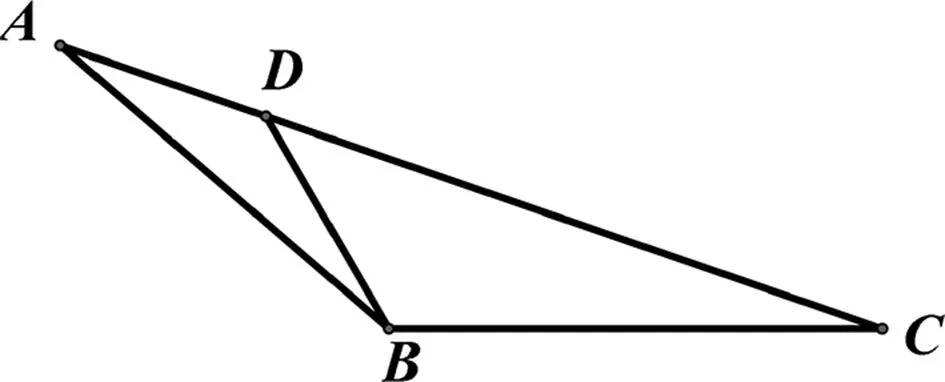
图1
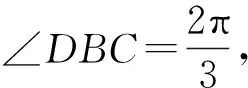
评注:本解法通过添加辅助线将角B分解为两个角,从而构造两个三角形相似,利用余弦定理构建边a的方程,实现了面积的转化计算.

图2
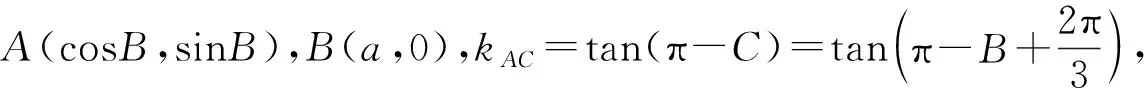
评注:本解法通过建立坐标系实现把解三角问题运用解析几何知识来求解.关键是几何条件代数化,其中,以B为原点的好处是可以根据AB=1把点A看单位圆上点,用角B巧设点A坐标,利用直线AC斜率表达式,把边a关系转化成角B的三角函数,进而通过AC距离公式计算sinB,最终转化成面积.
3.试题推广
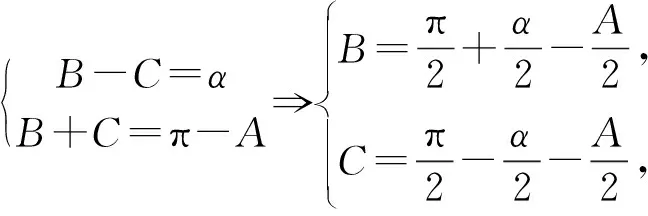
借鉴解法二的证明,我们可以得到更一般的结论.
推广在△ABC中,AB=c,AC=b,其中b>c且B-C=α>0,则△ABC的面积为
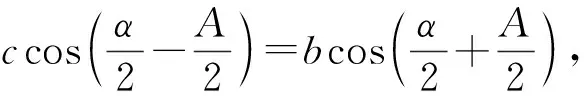
猜你喜欢
中学生数理化·高一版(2023年3期)2023-03-23 01:34:42
新高考·高三数学(2022年3期)2022-04-28 08:41:42
海峡姐妹(2020年2期)2020-03-03 13:36:30
海峡姐妹(2019年11期)2019-12-23 08:42:20
中学数学研究(江西)(2019年6期)2019-07-08 10:47:04
海峡姐妹(2019年6期)2019-06-26 00:52:32
中学生数理化·高一版(2018年6期)2018-07-09 06:00:56
海峡姐妹(2018年1期)2018-04-12 06:44:32
海峡姐妹(2017年4期)2017-05-04 04:03:52
海峡姐妹(2017年1期)2017-02-27 15:22:17

