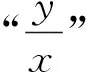构造齐次式巧解解几中的斜率之和(积)问题

江苏省如皋中学 (226500) 曹春茂

分析、解决直线与圆锥曲线交汇中，具有公共点的两条直线的斜率之和或斜率之积问题时，我们经常采用的就是“设而不求”技巧，对字母形式的代数运算以及推理能力的要求较高.为了简化运算，优化解题思维过程，现给出一种具有创新性的方法——在适当建立新的平面直角坐标系的基础上，借助“构造齐次式”，可巧妙处理此类问题.这种创新方法能够引导我们不断探索新颖别致的解法，培养探索精神，同时可帮助我们提升数学核心素养.

典型问题已知P是平面内的一个定点，圆锥曲线C上有两动点A,B，证明：直线PA与PB斜率之和(或积)为定值.

解题步骤：(1)在公共点P处建立新的平面直角坐标系(横轴与原来的横轴平行或重合，正方向相同；纵轴与原来的纵轴平行或重合，正方向相同)，则可将原问题等价转化为在新系下，证明直线PA与PB斜率之和(或积)为定值.

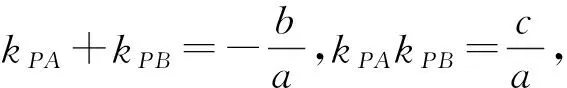
特别注意：若给定直线PA与PB斜率之和(或积)为定值，证明直线AB恒过定点.需要先在新系下，证明直线AB恒过定点；再在原坐标系下，具体分析定点的坐标.

图1

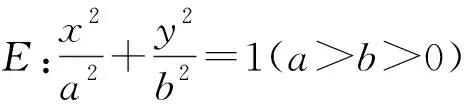
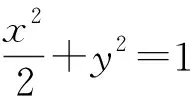
(2)当直线PQ经过坐标原点时，易知直线AP与AQ斜率之和为2.

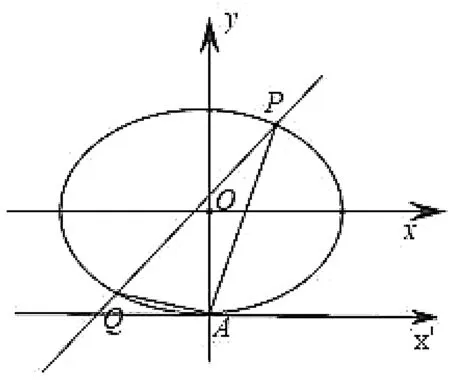
图2

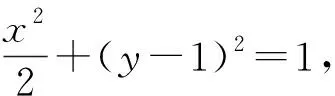
在新系下，设直线PQ的方程为mx+ny=1，则根据直线PQ经过点(1,2)可得m+2n=1.

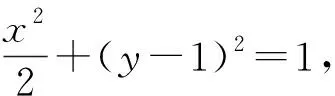
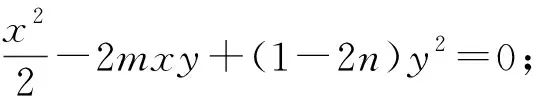
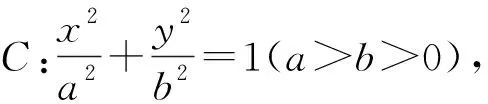
(1)求C的方程；(2)设直线l不经过P2点且与C相交于A,B两点，若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

(2)先分析直线l不经过坐标原点的情形.

图3

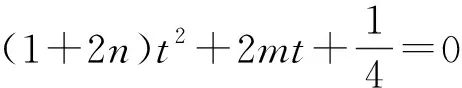
评注：第(2)问巧解，首先是在新坐标系下，通过“构造齐次式”，结合题设得到参数m,n满足的关系式2m-2n=1，进而得到直线l过定点(2,-2)；然后回归到原坐标系下，即可顺利获得直线l过定点(2,-1).

(1)求抛物线的方程；(2)已知C(0,-2)，若直线y=kx+2与抛物线交于A,B两点，记直线CA,CB的斜率分别为k1,k2，求证：k1k2+k2为定值.

解析：(1)易得抛物线方程为x2=2y(过程略).

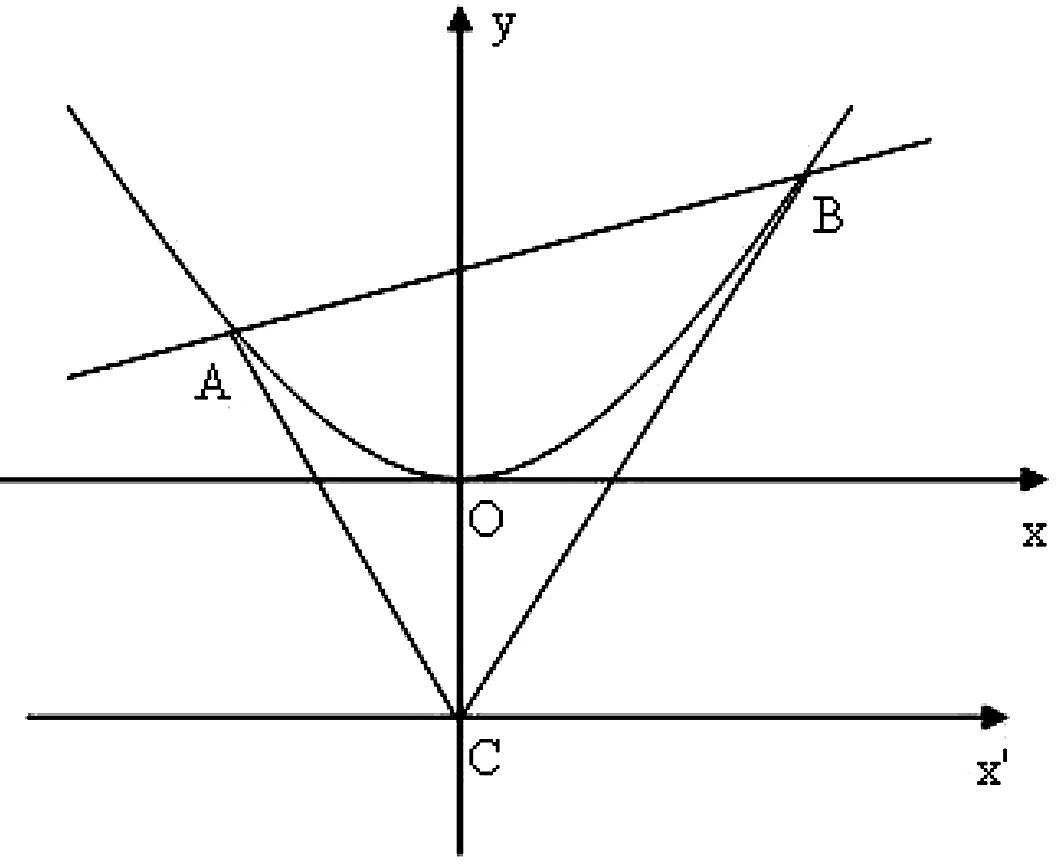
图4

(2)如图4，在点C处建立新的直角坐标系x′Cy，则在新系下抛物线方程为x2=2(y-2).易知直线AB不经过坐标原点.

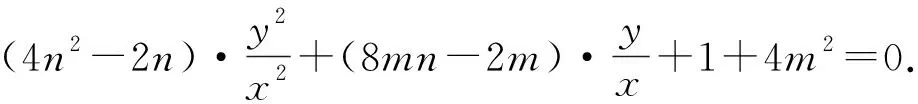
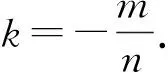
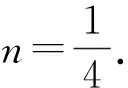
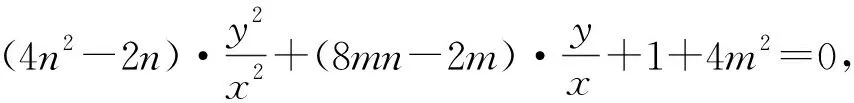
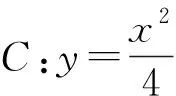
(1)求直线AB的斜率；(2)设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程.

解析：(1)直线AB的斜率为1(过程略).

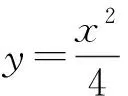
若直线AB经过坐标原点，则易知A与B的坐标分别为(0,0),(4,4)，又因为点M(2,1)，所以易检验知此时AM⊥BM不成立，从而必有直线AB不经过坐标原点.

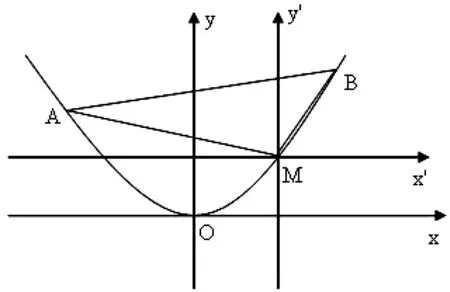
图5

在新系下，设直线AB的方程为mx+ny=1.

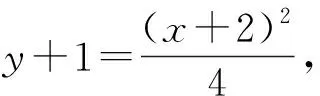
评注：一般地，若在点(a,b)处建立新的平面直角坐标系，则原来的抛物线x2=2py，在新系下抛物线的方程为(x+a)2=2p(y+b)；新系下的曲线方程f(x,y)=0，在xOy坐标系下曲线方程变为f(x-a,y-b)=0.