一道“推理”与“运算”并重的好题*
浙江大学附属中学丁兰校区 (310021) 陈作国 施刚良
1.试题呈现
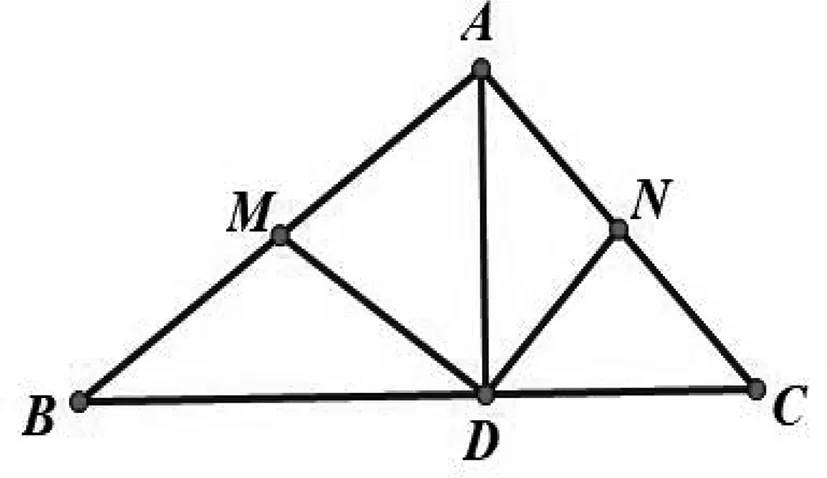
图1
如图1,在△ABC中,AB=8,AC=6,AD⊥BC,M,N分别为AB,AC的中点.
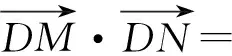
-6,求|BC|;
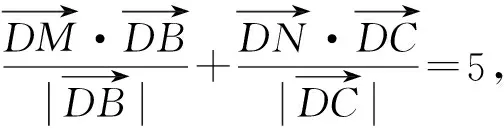
分析:这是一道“推理”和“运算”并重的高质量解答题,考察的内容非常多,简约而不简单,对数量积的四种形式(数量积的定义、数量积几何意义、极化恒等式、数量积坐标化)都有考察,学生在解决问题过程中,对数量积概念的理解稍有不慎就会出错,能有效地检测学生的数学思维能力.由于学生的数学运算能力较薄弱,数学推理素养不容乐观,涉及到要想想或转几个弯的问题往往选择“跳过去”,这是导致此题得分率偏低的原因.
2.解法探究
下面介绍几种解法:
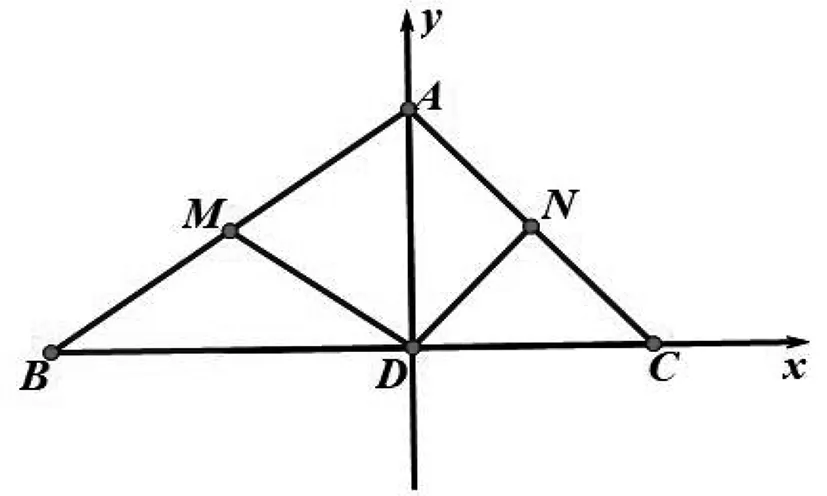
图2
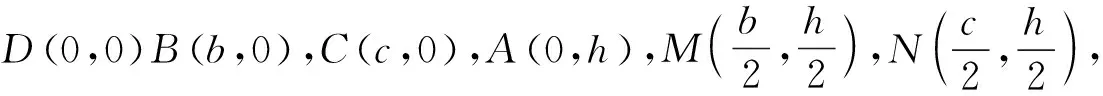
评注:建坐标系是学生处理向量问题的“杀手锏”,但是学生的数学运算素养又往往难达要求,本题主要的“拦路虎”是怎么利用bc+h2=-24,b2+h2=64,c2+h2=36这三个式子.其实,单个的解b,c,h还是有困难,通过整体消元的思想解决相对运算量下降.而且要达到这个目的,还要将BC=c-b平方(这对学生的数学运算、逻辑推理能力提出了很高的要求).从而通过整体消元,求得结果.
笔者在试卷讲评时,有学生还提出可以用极化恒等式加以解决,这种解法笔者事先没想到过.于是,就让他说说具体的解决过程:
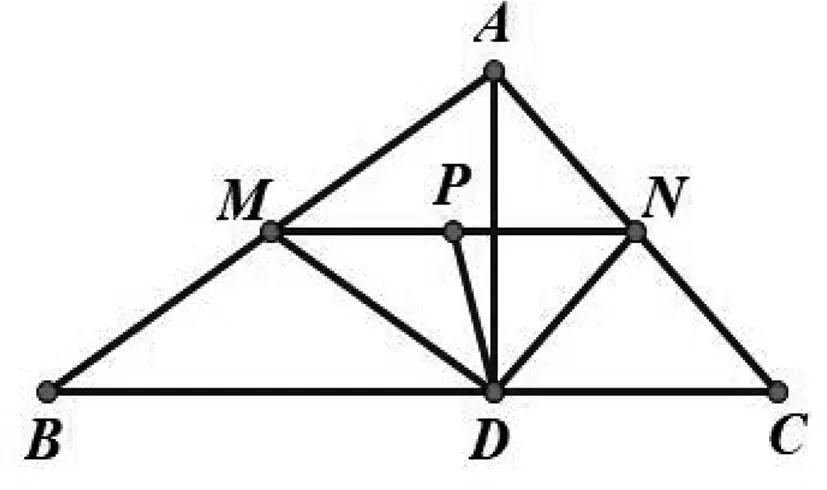
图3
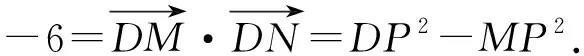


图4
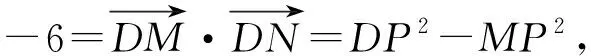
受上述利用向量等式求DP的长度的启发,课后笔者想到更加简洁的方法:

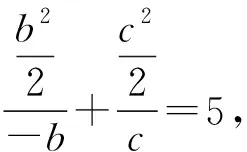
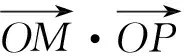
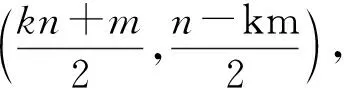
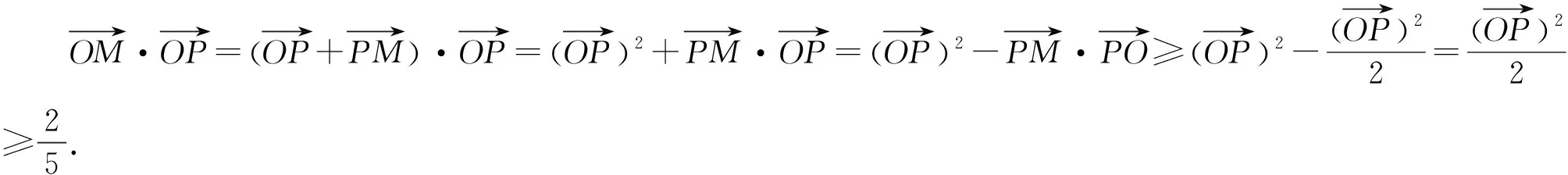
此题原来为填空题,笔者将之改为解答题,属于“小题大作”.主要想考察学生的数学运算能力和逻辑推理能力.所以,在平常的教学实践中,要将提高学生的推理和运算能力摆在中心地位,让学生多转几个弯或自己努力将结果算出来,这是我们在课堂实践中要舍得花时间做的.
3.教学反思
数学运算是逻辑推理的基础,同时逻辑推理的完成往往要借助数学运算.数学运算与逻辑推理是数学核心素养之一,我们在平常的复习实践中要合理地处理好两者之间的关系,这样才可以提高复习的有效性.

章建跃先生也认为,“推理是数学的‘命根子’,运算是数学的‘童子功’,推理与运算是数学的‘两个车轮子’”.所以,我们在数学教学中,要通过习题将推理与运算落实到位,要舍得花时间,这样做才可能让两个车轮子“齐头并进”,我们的教学才是有效的.同时也能提高学生的理性思维,这是数学育人的目的.

