共焦点的椭圆与双曲线的一个性质及应用
2022-04-11 10:06浙江省嘉善第二高级中学314100鲁和平
中学数学研究(江西) 2022年4期
浙江省嘉善第二高级中学 (314100) 鲁和平
圆锥曲线是高中数学的重要研究对象,其中具有相同焦点的椭圆与双曲线更是引人瞩目,耐人寻味.如果我们深入研究,就会得到它的一个十分有用的性质,运用好这个性质,将使不少问题就迎刃而解.

图1


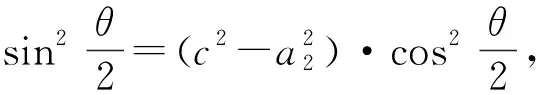
下面给该结论的应用.
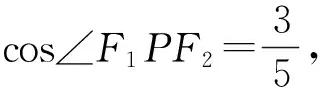
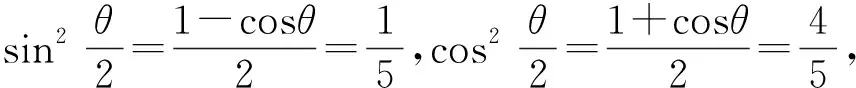
例2 已知F1,F2为椭圆与双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=60°,则该椭圆和双曲线的离心率之积的最小值是( ).

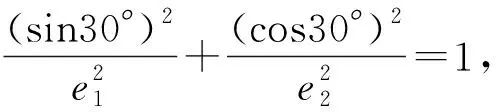


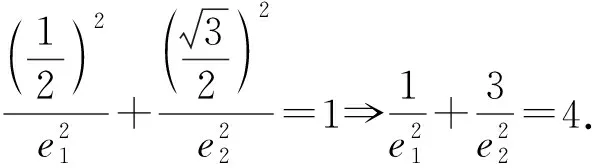
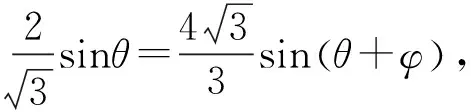
例4 已知F1,F2为椭圆与双曲线的公共焦点,P是它们的一个公共点,且满足∠F1PF2=45°,则椭圆的离心率e1和双曲线的离心率e2之积的最小值为( ).

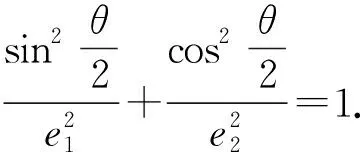

A.m>n且e1e2>1 B.m>n且e1e2<1
C.m
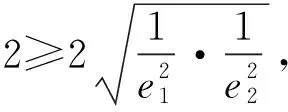
猜你喜欢
辽宁教育(2022年6期)2022-05-05
江南诗(2021年4期)2021-08-30
大众摄影(2021年2期)2021-01-29
疯狂英语·新读写(2021年1期)2021-01-29
中学生数理化(高中版.高考理化)(2019年3期)2019-04-25
课程教育研究·学法教法研究(2016年30期)2017-05-05
浙江林业(2016年5期)2016-11-30
新课程·上旬(2015年3期)2015-06-03
表面工程与再制造(2014年2期)2014-02-27

