两道圆锥曲线题的思考与结论推广

安徽省砀山中学 (235300) 蔡 聪

文[1]以2020年高考数学全国卷Ⅰ理科第20题和2020年高考数学山东卷第22题为例，介绍了齐次化方法在解决圆锥曲线中关于斜率之和为定值或斜率之积为定值的问题中的应用，并归纳了齐次化方法解题的步骤，可操作性强.经过笔者思考，借助于齐次化方法将两道题的结果推广到一般的情况，探究如下：

一 问题探究及结论推广

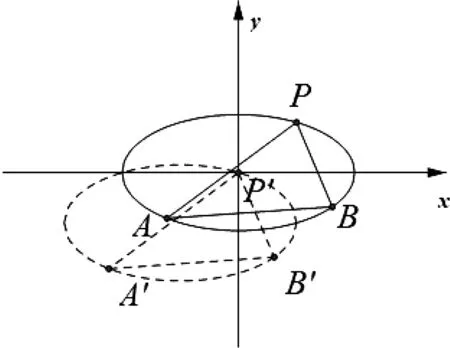
图1

上面的分析过程亦证明了下面结论成立：

评注：通过联立椭圆与直线方程，构造齐次方程A(y-y0)2+B(y-y0)(x-x0)+C(x-x0)2=0，证明了当直线PA与PB的斜率之和为定值时，随λ取值不同，直线AB存在定点或定值的情况.以该结论为背景的高考题还有2017年高考数学全国1卷理科第20题.故对高考题，不能仅仅解答出来就满足了，还应充分利用归纳与类比的思想，将结论推广，体会数学发现的过程.

对于斜率之积为定值，是否有类似的结论？

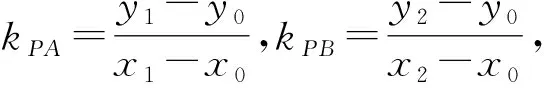
评注：2015年高考数学陕西卷文科第20题所考查的便是此结论的特殊情况.

同样地，若直线AB斜率为定值，也可以得到如下结论：

二 关于圆锥曲线高考备考的一点思考

1 加强方法训练，提高应用意识

对于斜率和为定值或积为定值的圆锥曲线模型，相较于常规解法(联立消元，韦达定理)，齐次化方法的步骤简洁，计算量少.教师在教学时，不应开门见山，而是通过比较两种方法的优缺，让学生去接受、练习和掌握.

2 挖掘试题背景，培养必备能力

数学家波利亚说“数学问题的解决仅仅只是一半，更重要的是解题之后回顾”，他把解题作为培养学生数学才能和教会学生思考的一种手段与途径.这种训练不同于单纯的题海战术，而是选取一个有意义又不复杂的题目，帮助学生深入挖掘试题的各个侧面，使学生通过这个题目，触类旁通，获得解题的一般思考方式.尤其是高考题这个宝藏，学习过程中，应不仅限于解题，更要剖析问题背景，对结论进行拓展，延伸，寻找特殊情境下的一般规律，这样学生才能在解题过程中提高发现和提出问题的能力、分析和解决问题的能力.

3 关注问题本质，发展核心素养

很多学生在处理圆锥曲线问题时，往往会出现有思路，但是计算受阻，或者计算得不到想要的结果，这是由于运算素养的缺失所造成的，《普通高中数学课程标准(2017年版2020年修订)》提出了数学的六大核心素养，其中数学运算既基础又重要，教师应在观察式子结构，明确计算方向，选择计算方法，有效化简，彻底化简等方面做足功课，在以后的教学中，应鼓励学生增强信心，不怕困难，勇于攻坚克难.