将学生从“前置概念”中解脱出来

高娟萍

【摘 要】学生在生活中对周围事物的观察和反思，会根据个人的性格和思维习惯形成一些独特的见解，当大量相似的现象汇聚到一起，原先的观念就会更加根深蒂固。久而久之，随着学生的心理不断发育，就会形成固定的思维定式而难以改变。

【关键词】认知结构 前置概念 教学策略

国外一些心理学家将学生正式接触某种概念之前，根据零碎的记忆和片段化的感知连缀起来的印象定义为“前概念”。显然，学生头脑中的前概念是浅薄而片面的。而建立在这些前概念之上的认知结构和价值体系大都是扭曲的，而且这种扭曲会带有一些标志性的错误，我们可以称之为“前置概念”或“偷换概念”。

“前置概念”会对学生的学习产生极大的危害，主要体现在当正确概念出现时，学生会发现与原有设想格格不入，甚至大相径庭。此时，由于前置概念的先入为主和排异反应，学生对新知极可能消极回避甚至正面抵触，在心里筑起一道自卫的屏障，这就严重影响了学生对新知的接纳与认同。为此，教师在教学正确概念前，必先破除学生对前置概念的迷信，从根基上打开突破口，让真知进入学生的意识内核。下面，笔者将结合个人的教学实践浅谈自己的一些尝试性做法。

一、经历操作活动，对错误认知釜底抽薪

教学中，教师应该创设适应学生学习需要的操作活动，从知识源头出发，引导学生通过动手实践来验证真知、求取真经。通过实践活动中自然生成的公理性结论，可以让学生看清自己前置概念之下的错误，以及与真实概念之间的差异，在实践结果的铁证对质下，学生“错误概念”的根基被彻底击溃和瓦解，原有认知结构也被彻底摧毁，学生开始重新构建认知体系，以便适应当前对新概念的接受和收纳。

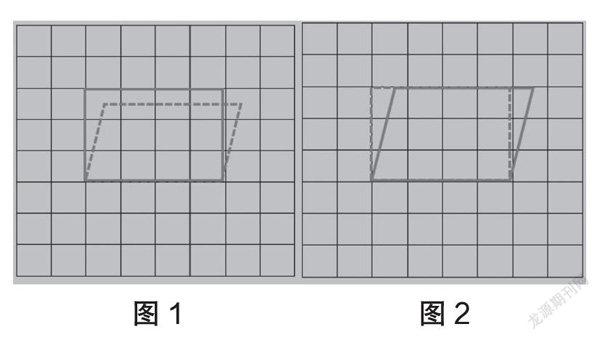
例如，教学“平行四边形的面积公式”时，受长方形面积计算方法的负迁移，以及这种思维方式的天然排斥性影响，学生会将新概念进行同化和收服，得出“平行四边形的面积 = 底×邻边长”的前置概念。这时教师就可以采用实践操作法——将一个平行四边形拖拉变形成一个长方形，然后在网格线中勾画出前后轮廓。学生通过操作就会发现，平行四边形变形成对应边长和周长不变的长方形后，长方形的长仍是平行四边形的一边，宽则是另一条邻边，用平行四边形的两邻边相乘得出的就是变形后的长方形的面积。但是通过网格线上对比反映出的形变经过，可以直观发现，变形后原图的面积扩大了（如图1），也就是说，原平行四边形的面积小于现在的图形。所以，计算平行四边形的面积时，运用“底×邻边”的算法是错误的。这时，教师再进一步指导学生在平行四边形旁边画出等面积的长方形（如图2），新建的长方形与平行四边形共底，画图时根据方格数的累加合并，来不断调节两个图形的面积差距直至完全相等，通过一番直观对比，学生会发现当两图面积相等时，长方形的宽等于原平行四边形的高。因此推断，长方形面积=长（平行四边形的底）×宽（高），由于两图面积相等，于是推知，平行四边形面积=平行四边形的底×高。这样一来，平行四边形的面积公式被操作导出并确立，先前关于其面积算法的“前置概念”被彻底攻破，学生从零开始重新建立起对平行四边形面积公式的理解。

图1               图2

二、变式训练，让认知变得更加全面

小学生的认知水平很低，于是很多的“前置概念”也就乘虚而入，疯狂滋长。教师应该举出一些反差鲜明的反例和特例，让学生“长长见识”，让学生强烈意识到，概念原来不止这一种面目，也不止这一种形式，还可能以其他非常规的形式出现，从而冲破经验藩篱的束缚，修补和完善自己的认知结构，使其不再有“漏洞和破绽”。

例如，在教学“认识三角形的底和高”时，许多学生想当然地望文生义，“错把冯京当马凉”，认为只是“底下的边”才是底，竖直方向的垂线段才是高。为了扭转这种片面的观点，教学时，教师利用课件对三角形进行动态旋转，让学生观察到三角形的底和高在相对位置不变的情况下，它们在画面中呈现的角度却发生着任意角度的旋转（如图3）。通过观察，学生明白，不能单靠视觉上的竖直来判断是否属于“高线”，只要和底构成垂直关系，且经过底边对应的顶点，就是三角形的高。同理，也不能单凭水平方向就认定三角形的底，三角形的三条边均可构成三角形几何学上的底，而不能遵循视觉效果上的“底下”;高也是如此，只要是从顶点出发向对边引出的垂线段，就构成几何意义上的高，而不能遵循视觉效果上的直立高度。通过变式，学生对三角形的底和高的真实概念就会有深刻的认识。

图3

三、利用亲和因子，让缺陷变优势

奥苏贝尔认为：“有意义的学习，就是符号化的新知按照学习者的编码规则进入学习者的头脑中，并与原有认知结构融为一体。”学生在日常生活和学习中积累的经验就是承载新知的容器，新知介入前的前置概念也可以作为容器的入口。此时，教师应努力从学生的已有经验中寻找与新知能对接的亲和因子，让原有经验产生正迁移作用，加速学生对新知的理解和内化。

例如，在教学“倒数”这部分内容时，教师如果询问学生“何为倒数”，学生第一反应一定是“倒数就是颠倒过来的数”，这是因为学生处于形象思维阶段，也就是具体运算阶段，他们看问题只在乎表面的直观现象，不会去关注内在的深层含义，所以一看到倒数，则很容易从字面上去理解，从颠倒这个词来理解数字的意义。这样的“前置概念”虽然是想当然，但是从某种程度上说，也无意间说明了倒数数学本质之外的非显著特征。教师不妨沿着学生的这一直觉猜想，将其作为“前置概念”中的可转化分子，顺势而为，出示2 —5的倒数是5 —2，6 —7的倒数是7 —6，接着追问：“0.6与1.6的倒数各是什么数？”“6和16的倒数又是什么数？”通过前面的诱导，学生可能会设法进行转化，将这些小数和整数化成分数形式，再按照颠倒分子分母的位置来求出倒数，但是这样做带来的麻烦，也会促使學生去寻找它们内在的普遍数学规律，尝试直接通过这种规律来推导倒数，从而产生探求倒数概念本质的强烈动机，加深其对倒数概念的理解。

四、完善知识结构，让零散变系统

学生的“前置概念”虽然会阻挠其对新知的接受，但是并不可怕，因为学生的认知观尚未彻底定型，前置概念也是发展变化的，里面隐含着学生的许多低层次的思考。如果教师能辩证统一地看待前置概念，找到其中的突破口，经过诱导和转化，也可以将其变成积极的有正向意义的元认知，甚至是构建新知不可缺少的一环，把它和新知融合起来，这样，学生对知识的理解会更加深刻全面。

例如，在教学“圆锥的认识”时，师生一起探讨。

师：我们已经了解了圆锥，思考一下圆锥的侧面展开后的图形是什么。

生1：是三角形！

生2：我也赞同，说得更具体些，展开后会是一个等腰三角形。

师：是吗？这是什么道理？

生3：（迫不及待地证明）圆锥的顶点到底面边上的所有连线段等长，因此对应着三角形顶点到底边两端等距。所以，圆锥的侧面铺开后是一个等腰三角形。

学生的解释虽很牵强，却振振有词，而且似乎有理有据，虽然只是一种肤浅的直觉，却也是经过理性思考的。起码，他们发现圆锥的母线长度恒等。

师（继续追问）：等腰三角形只有顶点到底边两端点等距，顶点和底边的连线是不是处处相等呢？

学生马上动手验证，发现长短不一。

师：找到破绽了？那么真相到底如何？

生4：那就要寻求一种顶点到底边连线处处等长的图形，这样才符合要求。

生4的回答让所有人茅塞顿开，大家纷纷开始着手画图，寻找目标……经过画图操作，最后一致确定是扇形。

在这一教学环节中，学生善思也善于发现，只是没有抓住平面图形的全部特征，离真相只有一步之遥，厚积才能薄发。因此在教学中，我们应该引导学生完善和修补原有认知，形成统一的认知结构。

综上所述，在教学中教师应尊重学生的前置概念，顺应学生的心理发展规律，通过智慧得体的举措，循循善诱、因势利导，不断完善和纠正学生的认知，启迪学生的智慧。