高中数学教科书“阅读材料”的教学与思考

陆娅君 袁涛 张和平

【摘 要】 “阅读材料”是开展探究性学习的重要素材，文章基于“双曲线的光学性质及其应用”内容开展教学并作出反思：将“阅读材料”融入课堂教学中，有利于数学思想方法的渗透、培养学生的数学应用意识和探究问题的能力.

【关键词】 数学教科书;阅读材料;双曲线的光学性质

《普通高中数学课程标准（2017年版）》指出，教学活动不应只限于讲授和练习，还应倡导阅读自学、独立思考、动手实践、自主探究、合作交流等学习数学的方式[1].教材中的“阅读材料”体现了教学内容的弹性，符合不同层次学生的发展，帮助学生掌握正文的内容，并能促使学生内化数学思想方法、培养学生的数学应用意识和探究问题的能力.数学教材中“阅读材料”不应该是被教学遗忘的角落，而应该成为教学改革的试验田[2].但在实际教学中，由于其不属于考试范围，大部分教师把它们当作学生课外学习的内容，不予以重视，忽略了“阅读材料”的教学价值和育人功能.本文以新人教A版高中数学教科书“阅读材料”中“双曲线的光学性质及其应用”为例，谈谈对阅读材料的使用与思考.

1 案例分析

1.1 依托教材，创设情境

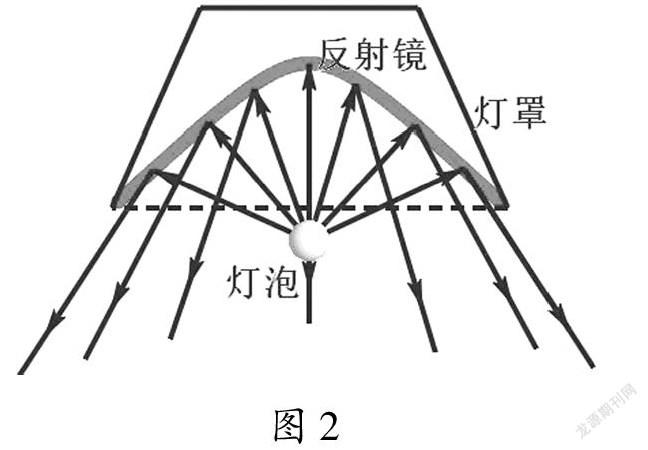
床头灯是利用灯泡照射，通过反射镜反射而散发出光的一种装置.灯罩不需要连接电源，上面装有能旋转的反射镜，反射镜的形状是双曲面，利用这样的装置就能散发出光了（如图1）.通过灯泡所在位置的纵截面，可以得到图1的纵截面图，如图2所示.

师：利用床头灯照射的原理是什么？

生：因为曲面型的反射镜将光线散发出去了.

师：这个反射镜的轴截面是一个怎样的图形？灯泡应该位于哪个特殊的位置？

生：可能是双曲线的一支，灯泡位于双曲线的焦点处.

设计意图 依托“床头灯照射”创设情境，引导学生分析其工作原理，进而抽象出双曲线模型，教师再结合双曲线的相关知识进行提问，将生活问题抽象为数学问题，让学生直观感受双曲线中光波的反射规律与焦点有关，提升学生数学的感知能力和数学抽象的核心素养.

1.2 阅读发现，直观验证

问题1 光的反射现象如果与双曲线的焦点有关，那么应该遵循怎样的反射规律？

在物理学中，焦点可以理解成是光线聚集的点.把床头灯装置中反射镜的轴截面抽象成双曲线的一支，把灯泡抽象成双曲线的一个焦点，把光线抽象成直线，得到图3.开启灯泡电源时，床头灯散发出了一束光线，实际上是由燈泡发出的.但从视觉效果上看，每一条光线就好像是从灯泡后面某个虚拟位置（即虚光源处）直接发出的，可以初步判定虚光源一定位于光线的反向延长线上.作出光线的反向延长线，得到虚光源F1，F1和灯泡所在位置F2是双曲线的两个焦点，如图4所示.图4直观地反映了光在双曲线内的反射规律：从双曲线的一个焦点发出的光线，经过双曲线反射后，反射光线是散开的，它们就好像是从另一个焦点射出的一样.

问题2 反射镜面与双曲线会有怎样的位置关系？

由物理学的相关知识可得，反射镜面与双曲线的位置关系是相切的.

问题3 如何直观地验证双曲线中光的反射规律？

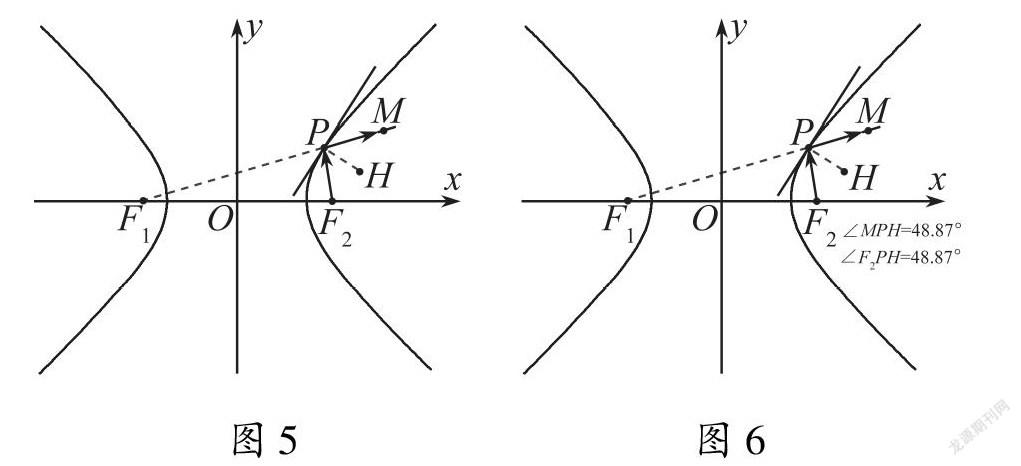
可以用几何画板直观验证：首先找到双曲线的一条切线，作为反射镜面;连接点F2和切点P，F2P就可以作为一条入射光线;作出反射镜面的法线PH之后，就需要观察反射光线PM的反向延长线是否经过点F1，如图5所示.图5         图6

问题4 用几何画板直观演示当点P在双曲线上运动时，MPH和F2PH会有怎样的数量关系？如图6所示.MPH=F2PH时，也就说明反射光线的反向延长线经过点F1.改变双曲线的形状，可以发现这两个角仍然相等.设计意图 根据生活现象猜想出光在双曲线内的反射规律，再用几何画板直观验证，尝试建立文字与图形的联系，促使学生透过现象看数学本质.经历数学知识抽象的过程，培养学生数学模型思想，发展学生数学抽象、直观想象的核心素养.

1.3 通过证明，深度探究

师：利用几何画板初步验证了光在双曲线内的反射规律，如何从数学的角度证明？

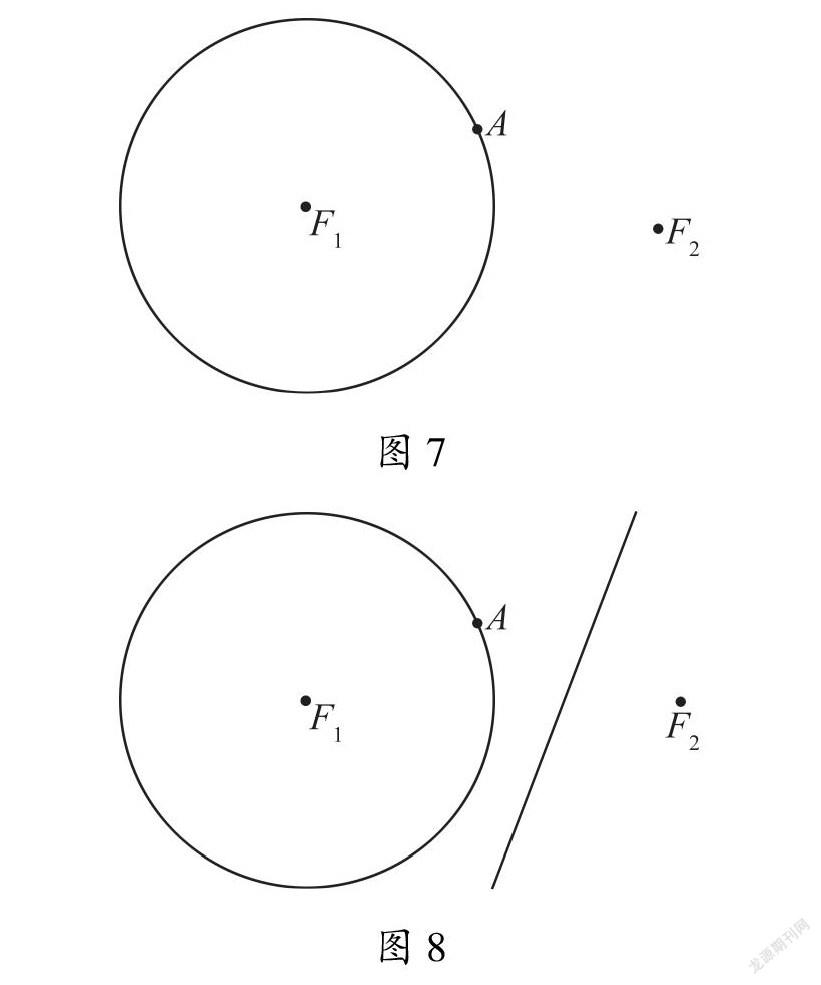
活动：已知圆F1和定点F2（定点F2不在圆F1上），在圆F1上随机取一点A，如图7所示.如何通过纸片对折的方式来做出线段AF2的垂直平分线？

只需要让点A和点F2重合即可，即对折两个点，由此便得到一条折痕，将折痕用笔画上颜色，如图8所示.

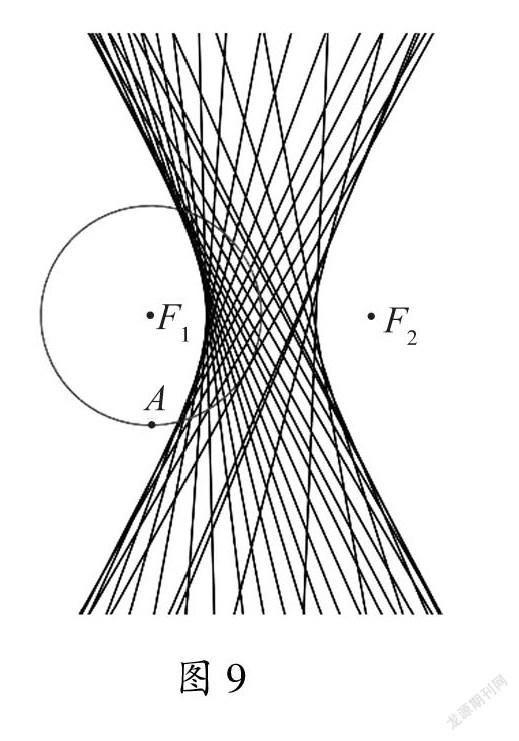
一直重复此操作过程，将点A绕圆周一圈，你有什么发现？如图9所示.

设计意图 让学生动手操作折纸活动，培养学生动手实践、合作交流、自主探究的能力;使学生在操作、观察、猜想的过程中，逐渐领悟折痕所在直线与双曲线的位置关系，自主构建认知结构.通过数学活动，让学生体验从具体到抽象的过程，促使学生对数学现象产生个性化的理解，培养学生直观想象、数学抽象的核心素养.

师：折痕所在直线与双曲线具有怎样的位置关系？

通过折纸活动发现折痕所在直线与双曲线相切.

师：如果折痕所在直线l与双曲线相切，那么直线l会作为一个什么图形出现？

直线l会作为反射镜面出现，但通过折纸活动和几何画板的验证得到的“相切”是不严谨的，需要进一步证明.

问题1 已知双曲线的左焦点F1与圆的圆心重合，双曲线的长轴长与圆的半径相等即2a（a>0），点A为圆上任意一点，如何证明折痕所在直线l与双曲线相切？

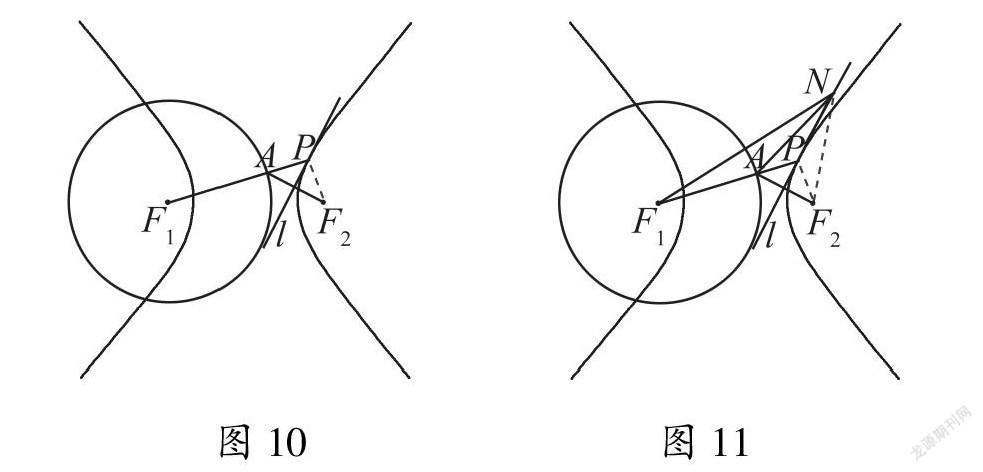
首先证明点P在双曲线上.如图10所示，直线PF1与l相交于点P;因为点P在线段AF2的垂直平分线上，所以连接PF2，由垂直平分线的性质可得|PA|=|PF2|;根据等量替换可得：|PF1|-|PF2|=|PF1|-|PA|=|AF1|=2a，又因为双曲线的长轴长为2a，所以点P是双曲线上的点.

师：点P既是双曲线上的点，同时也处于线段AF2的垂直平分线上，那么也只能说明点P是直线l与双曲线的一个交点，交点一定是切点吗？相交和相切最主要的区别是什么？

相交和相切最主要的区别是交点的个数问题.如果要验证相切的情况，就需要验证点P是直线l与双曲线唯一的交点.

师：如何证明一个点的唯一性？

如图11所示，在直线l上任取一个不与点P重合的点N.点N在线段AF2的垂直平分线上，所以满足|NA|=|NF2|.因为点N与点P并不重合，故而点N、点F1、点A可构成一个三角形，由三角形的性质可得：|NF1|-|NA|<|AF1|.由等量替换即得|NF1|-|NF2|=|NF1|-|NA|<|AF1|=2a，据此可说明点N到双曲线两个焦点的距离之差的绝对值小于2a，即点N在双曲线外部.因此，直线l上有且只有一个点P在双曲线上，所以直线l与双曲线相切，点P是切点.

问题2 已知双曲线的左焦点F1与圆的圆心重合，双曲线的长轴长与圆的半径相等即2a（a>0），如图12所示，求证：∠MPH=∠F2PH.图12

因为直线l是线段AF2的垂直平分线，所以|CA|=|CF2|，∠ACP=∠F2CP=90°，|PC|=|PC|，据此可得△CAP≌△CF2P（SAS），即∠APC=∠F2PC.因为∠APC=∠MPD，由等量替换可得：∠F2PC=∠MPD.因为PH⊥l，所以∠DPH=∠CPH，即可得∠MPH=∠F2PH.

据此可得双曲线的光学性质：从双曲线的一个焦点发出的光线，经过双曲线反射后，反射光线是散开的，它们就好像是从另一个焦点射出的一样.设计意图 利用几何画板与折纸活动验证双曲线的光学性质还不够严谨，需从数学的角度证明折痕所在直线与双曲线相切、∠MPH=∠F2PH，从而抽象出双曲线的光学性质，体现了数学学科结构严谨、逻辑性强的特征，培养学生数学抽象、逻辑推理的核心素养.借助图形进行证明，体现了数形结合的思想方法，培养学生直观想象的核心素养.

1.4 巩固拓展，体验价值

问题1 在问题情境中，利用床头灯散发出光时，为什么要将反射镜设计成双曲面的形状？灯泡应该位于哪个位置？为什么？

问题2 在反射式天文望远镜的内部，为什么要将副镜设计成双曲面的形状？主焦点和成像焦点应该位于哪个位置？为什么？

设计意图 对情境内容再次提问，帮助学生梳理知识脉络，更加清晰地认识双曲线的光学性质在床头灯中应用的具体原理.通过相似问题，让学生进一步巩固双曲线的相关知识，感受“双曲线的光学性质”在生活中的广泛应用，开拓学生的数学视野.

2 对“阅读材料”的思考

2.1 对案例的总结与反思

依托教材中“阅读材料”并结合生活现象创设情境，由此引入课题和提出相关的探究问题，接着利用折纸活动和几何画板验证双曲线的光学性质，帮助学生积累数学活动经验，进而发展学生直观想象的核心素养;再用数学方法证明性质，让学生经历完整的数学论证过程，发展学生数学抽象、逻辑推理的核心素养;最后让学生理解双曲线的光学性质在某些装置中的应用原理，培养学生的数学应用意识.2.2 滲透数学思想方法

“阅读材料”蕴含了丰富的数学思想方法，如“探究函数y=x+1x的图象与性质”中介绍了如何根据函数解析式研究函数图象以及根据函数图象探究函数的相关性质，其中渗透了数形结合的思想;“集合中元素的个数”中介绍了根据具体实例的计算思路进而推导出任意两个有限集合的并集中元素个数的计算公式，体现了从特殊到一般的思想.教师应当深入剖析“阅读材料”所蕴含的思想方法，并合理运用其进行教学，提高学生学习数学的能力.2.3 培养数学应用意识

教材中“阅读材料”的内容与社会生活、科技生产等有着紧密的联系.在教学中，教师应引导学生从数学的角度观察生活，用数学语言表达问题，体验数学的应用价值，促使学生形成数学应用意识.如“统计学在军事中的应用”让学生了解到利用样本估计总体能推断出在二战时期德军每月生产的坦克数目;“圆锥曲线的光学性质及其应用”还介绍了手电筒发光和电影放映机的工作原理，感悟生活处处皆数学.

2.4 培养探究问题能力

“阅读材料”设置了“信息技术应用”专题，其目的是希望教师尝试利用网络资源开展基于信息技术的教学.在运用数学软件探究问题的过程中，学生经历发现问题、提出猜想、独立验证等过程，能培养学生探究问题的能力.如“概率分布图及概率计算”“探究指数函数的性质”“利用信息技术制作三角函数表”等，都是可以借助信息技术进行探究性学习的素材.

教材中“阅读材料”蕴含着丰富的教育功能，教师应当主动挖掘这些资源，进行再创造、再组织，应用到课堂教学中，让学生在此过程中感受数学的魅力与价值.

参考文献

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2017：8283.

[2] 宋磊.重视教材阅读材料 提升数学核心素养——阅读材料“椭圆的一种应用”引发的探究课[J].数学通讯，2020（10）：2124.

作者简介 陆娅君（1997—），女，贵州遵义人，贵州师范大学硕士研究生;主要研究数学教育.袁涛（1994—），男，贵州遵义人，贵州师范大学硕士研究生;主要研究数学教育.

张和平（1974—），男，贵州从江人，博士，凯里学院理学院教授;主要研究数学教育与测量.