近年高考概率统计试题分析及2022年高三复习建议

王淼生 周翔

【摘 要】 通过对近年尤其近三年高考概率与统计试题的分析，对比新旧版教材（人教A版）相关内容的增减与编排次序，揭示概率与统计试题的命制特点，预测2022年高考试题的侧重点，提出2022年高三复习与备考建议.

【关键词】 试题分析;教材对比;命题特点;复习建议

《中国高考评价体系》是一个以价值为引领的、系统的、科学的评价体系，创造性地提出“一核四层四翼”，借以评价与检测考试目标实现的程度及考试要求达成的幅度.《普通高中数学课程标准（2017年版）》将概率统计作为四大主线之一，凸显概率统计在高中数学课程中的地位与价值.尤其2021年的全国高考试题，紧紧围绕《中国高考评价体系》的精髓与《普通高中数学课程标准（2017年版）》要求，实现“知识立意”到“能力立意”再到“价值引领、素养导向、能力为重、知识为基”转变，落实“立德树人、服务选才、引导教学”的目标.本文通过对近三年全国卷概率统计试题的综述及新旧版教材的对比，預测未来命题侧重点，为2022年高三复习备考提出一些建议.

1 近三年概率统计高考试题分析

1.1 全国卷概率统计试题综述及分布

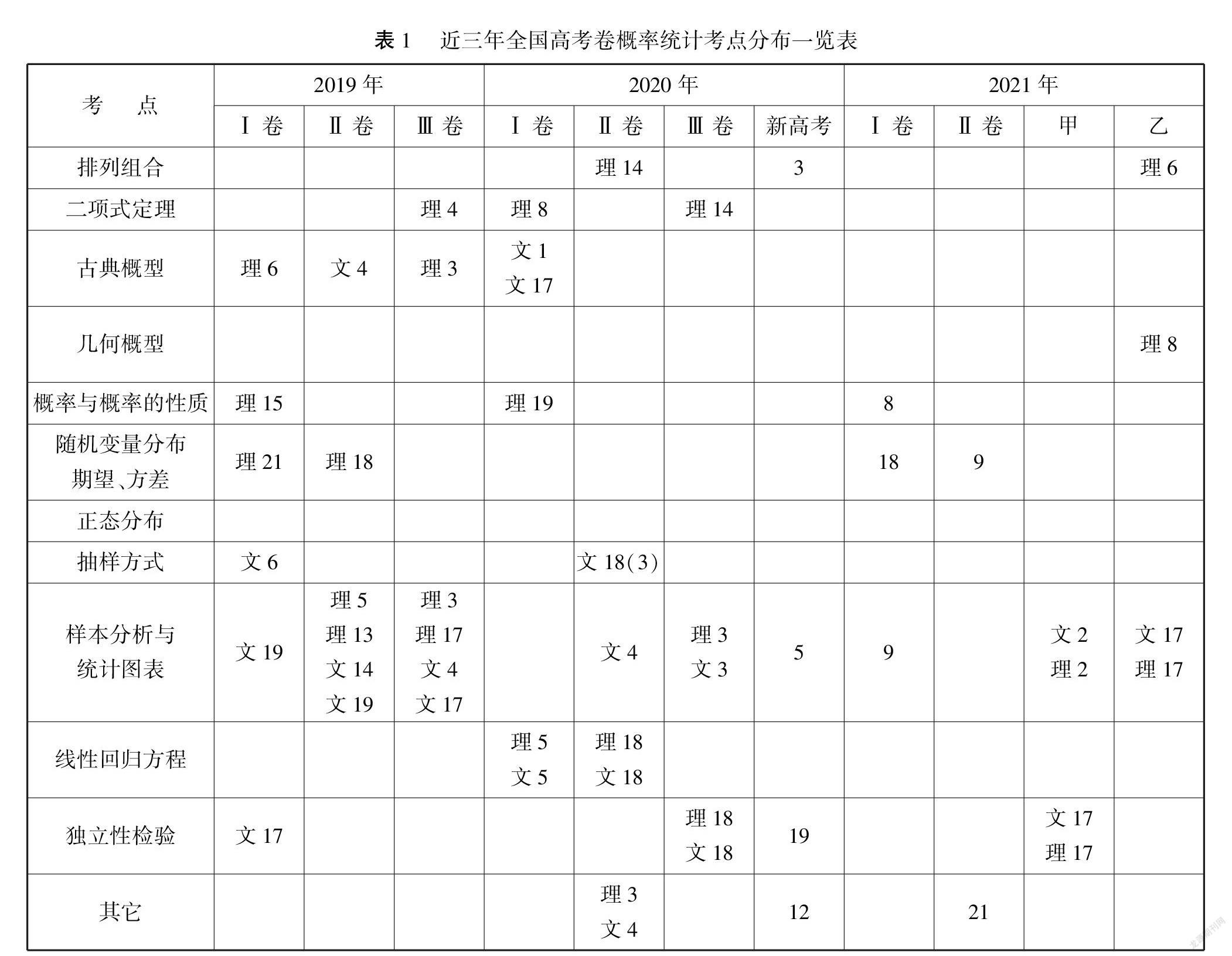
《普通高中数学课程标准（2017年版）》指出，概率统计主要内容包括：随机事件与概率、随机事件的独立性、获取数据的基本途径及相关概念、抽样、统计图表、用样本估计总体.概率统计（含排列组合）一直是高考的重点、热点内容，一般以“二小一大”三道试题呈现（具体分布情况见表1）.其中，随机变量的分布、期望、样本分析、统计图表及与其他知识的综合交汇成为热点.从新高考全国卷来看，2021年Ⅰ卷以考查独立性理解和运用独立性进行决策为主，Ⅱ卷推陈出新，借助导数工具研究概率取值范围，彰显《中国高考评价体系》中“四翼”要求——学科知识的综合性与交汇性，而旧高考模式的甲卷、乙卷，为了实现新旧高考顺利交接，整体呈现文理趋同，重心向统计倾斜.

1.2 全国卷概率统计高考试题命制特点

（1）重视相关核心概念的辨析考查

题1 （2021·全国新高考18）有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回的随机取两次，每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则（  ）.

A.甲与丙相互独立B.甲与丁相互独立

C.乙与丙相互独立 D.丙与丁相互独立

题2 （2021·全国甲卷理10）将4个1和2个0随机排成一行，则2个0不相邻的概率为（  ）.A.13   B.25   C.23   D.45

评注 题1考查事件独立性的概念，得分率较低.失分原因在于考生对独立性概念理解不够深刻，难以辨析独立性概念与条件概率之间的联系与区别.题2涉及古典概型，求解关键是将问题转化为两组相同元素的排列计数问题.

（2）强化阅读理解能力的考查题3 （2021·全国甲卷文2）为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如图1频率分布直方图：

根据此频率分布直方图，下面结论中不正确的是（  ）.

A.该地农户家庭年收入低于4.5万元的农户比率估计为6%

B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%

C.估计该地农户家庭年收入的平均值不超过6.5万元

D.估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间

题4 （2021·全国乙卷理17）某厂研制了一种生产高精产品的设备，为检验新设备生产产品的某项指标有无提高，用一台旧设备和一台新设备各生产了10件产品，得到各件产品该项指标数据如下：

旧设备和新设备生产产品的该项指标的样本平均数分别记为和，样本方差分别记为S21和S22.

（1）求，，S21，S22;

（2）判断新设备生产产品的该项指标的均值较旧设备是否有显著提高（如果-≥2S21+S2210，则认为新设备生产产品的该项指标的均值较旧设备有显著提高，否则不认为有显著提高）.评注 题3通过频率分布直方图考查考生对符号语言、图形语言的阅读理解能力.题4需要对表格中蕴含的信息进行提取、加工.考查考生对数据的分析处理能力及作出统计推断的能力.（3）凸显知识点的综合性与交汇性考查

题5 （2021·全国Ⅰ卷18）某学校组织“一带一路”知识竞赛，有A，B两类问题，每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束.A类问题中的每个问题回答正确得20分，否则得0分;B类问题中的每个问题回答正确得80分，否则得0分，己知小明能正确回答A类问题的概率为0.8，能正确回答B类问题的概率为0.6，且能正确回答问题的概率与回答次序无关.

（1）若小明先回答A类问题，记X为小明的累计得分，求X的分布列;

（2）为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由.

题6 （2021·新高考全国Ⅱ卷21）一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代……，该微生物每代繁殖的个数是相互独立的且有相同的分布列，设X表示1个微生物个体繁殖下一代的个数，P（x=i）=pi（i=0，1，2，3）.

（1）已知p0=0.4，p1=0.3，p2=0.2，p3=0.1，求E（X）;

（2）设p表示该种微生物经过多代繁殖后临近灭绝的概率，p是关于x的方程：

p0+p1x+p2x2+p3x3=x的一个最小正实根，求证：当E（X）≤1时，p=1，当 E（X）>1时，p<1;

（3）根据你的理解说明（2）问结论的实际含义.

评注 题5考查分布列、期望并通过期望作出科学决策.题6的难点在于信息的读取和加工.先构造函数f（X）=p0+p1x+p2x2+p3x3-x，发现f（1）=0及导函数对应方程的判别式大于零（存在两个异号根）.E（X）≤1与E（X）>1的本质反映了导函数在x=1处的符号特征.再结合图象，借助函数单调性解决问题.题6具有较强的综合性与交汇性，有利于考生展示才华，落实立德树人、服务选才、引导教学的目标.

2 概率统计知识在新旧版教材中的对比

概率统计知识已经成为公民的必备常识.随着大数据时代的到来，统计与概率地位得到進一步提升.在高三复习中，要密切关注、仔细对照新旧版本教材在内容增减及编排次序等方面的差异.比如，最新版教材将概率统计作为高中数学四大主线之一，贯穿于必修、选择性必修和选修课程之中;将数学建模、数学文化渗透在在整个高中数学之中.以人教A版为例，增加了分层随机抽样的样本均值和样本方差;百分位数;样本点，有限样本空间;乘法公式，全概率公式等内容.删减了统计中的系统抽样、变量的相关性;概率中的几何概型;计数原理中的计数原理解决简单的实际问题等内容.降低了概率中的超几何分布及计数原理等内容的考查要求.调整了一些内容的编排次序，比如对事件的独立性与条件概率等概念，人教A版新教材将“相互独立事件”概念安排在普通高中教科书数学必修第二册第十章“概率”第10.2“事件的相互独立性”中;将“条件概率”编排在普通高中教科书数学选择性必修第三册第七章“随机变量及其分布”第7.1“条件概率与全概率公式”中.人教A版旧教材将独立事件安排在条件概率之后，而人教A版新教材将独立事件安排在条件概率之前，这是人教A版新旧教科书在“独立事件”编排上最为显著的变化.借此警醒一线教师对比教材、研究教材，密切关注教材内容编排次序的变化.这正是高考命题专家命制上述题1的缘由（详见文[1]）.3 对2022年全国高考概率统计的预测

预计2022年高考对概率统计的考查主要聚焦基本概念、基本公式的理解、应用以及运算求解能力和数据处理能力. 考点主要有两大类：一类是以排列组合、二项式定理、古典概型、离散型随机变量的分布列及数学期望的概率计算问题. 另一类是以抽样方法、样本的频率分布、样本数字特征、统计图表、回归方程、独立性检验为主的统计案例问题. 选择题、填空题预计仍以考查核心概念为主，难度适中;解答题未必固定在第19题的位置，可能后移至20或21题，加大综合考查力度，需要引起重视.

3.1 考查传统文化背景下的样本点分析

题7 （2019·全国Ⅰ理6）我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，

如图2就是一重卦.在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是（  ）.

A.516    B.1132

C.2132    D.1116

评注 弘扬中华优秀传统文化、革命文化和社会主义先进文化是新高考落实立德树人的重要载体.近年来以传统优秀文化为背景的概率统计试题屡见不鲜. 题7就是从我国古代典籍《周易》中的“卦”演变而来，需要考生认真审题，重视阅读，快速抓住概率实质，准确设定有限样本空间，列出样本点，运用古典概型公式快速求解.3.2 考查时代热点下的数据加工与处理能力

题8 （2018·全国Ⅰ卷理3）某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：

则下面结论中不正确的是（  ）.

A.新农村建设后，种植收入减少

B.新农村建设后，其他收入增加了一倍以上

C.新农村建设后，养殖收入增加了一倍

D.新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半

评注 概率统计源自生产、生活，同时又解决生产生活中的实际问题.新高考尤其关注时代热点，比如新农村建设、医疗卫生、药品安全、环境监测、质量检测等.题8就是典型的新时代新农村经济建设问题，要求考生对现有数据进行分析与处理，从而得出结论.

3.3 考查运算灵活性及思维敏捷性

题9 （2017·新课标Ⅰ卷理19）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）.根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N（μ，σ2）.

（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在（μ-3σ，μ+3σ）之外的零件数，求P（X≥1）及X的数学期望;

（2）一天内抽检零件中，如果出现了尺寸在（μ-3σ，μ+3σ）之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查.

（ⅰ）试说明上述监控生产过程方法的合理性;

（ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：

9.9510.129.969.9610.019.929.9810.04

10.269.9110.1310.029.2210.0410.059.95

经计算得=116∑16i=1xi=9.97，s=116∑16i=1（xi-）2=116（∑16i=1x2i-162）≈0.212，其中xi为抽取的第i个零件的尺寸，i=1，2，…，16.

用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需对当天的生产过程进行检查？剔除（-3，+3）之外的数据，用剩下的数据估计μ和σ （精确到0.01）.

附：若随机变量Z服从正态分布N（μ，σ2），则P（μ-3σ<Z<μ+3σ）=0.9974，0.997416≈0.9592，0.008≈0.09.

评注 深入分析近年来的高考试题，不难发现高考对统计数据的分析和处理要求明显提高.题9需要考生理解运算对象，掌握运算法则，借助已有数据，实施局部调整，探究运算方向，选择运算方法，优化思维品质，提升学生数学运算素养.3.4 考查独立性检验中的小概率思想

题10 （2020·全国Ⅲ文18、理18）某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：

锻炼人次空气质量等级        [0，200]（200，400]（400，600]

1（优）216252（良）510123（轻度污染）678

4（中度污染）720

（1）分别估计该市一天的空气质量等级为1，2，3，4的概率;

（2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）;

（3）若某天的空气质量等级为1或2，则称这天“空气质量好”;若某天的空气质量等级为3或4，则称这天“空气质量不好”.根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？

人次≤400人次>400空气质量好空气质量不好

附：K2=n（ad-bc）2（a+b）（c+d）（a+c）（b+d），

P（K2≥k）0.0500.0100.001k3.8416.63510.828

评注 值得关注的是文科卷已经连续多年考查独立性检验问题，题10就是其中经典案例之一.这类试题通过对收集数据的分类变量分析，进行独立性检验，辅助统计推断.通常第（1）问考查频率估计概率的思想方法，用样本估计总体;第（2）问考查利用2×2列联表进行独立性检验的思想方法，即小概率反证法思想，属于统计推断.3.5 考查开放性情境中的科学决策能力

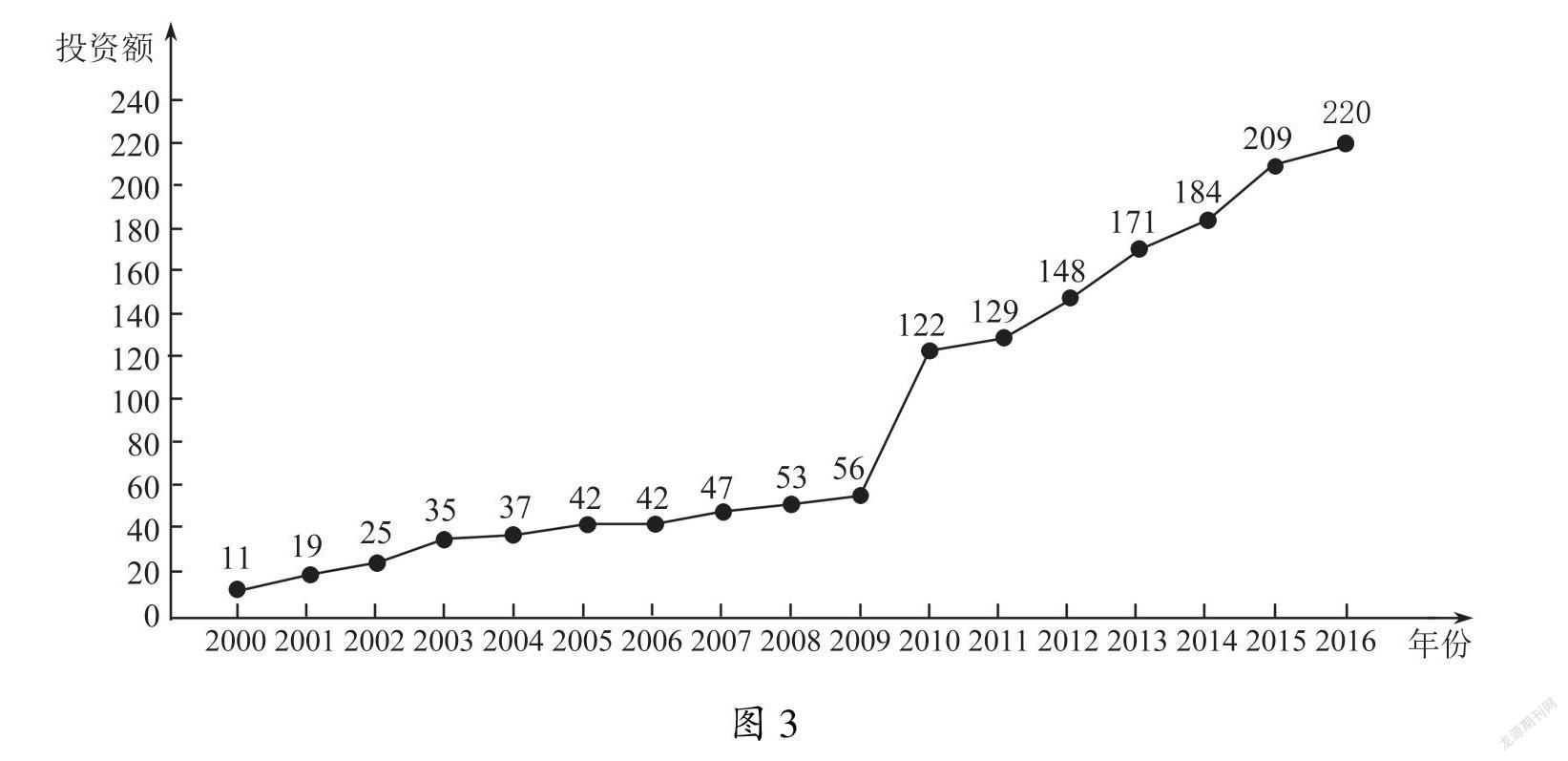
题11 （2018·全国卷Ⅱ理18）图3是某地区2000年至2016年环境基础设施投资额y（单位：亿元）的折线图.

为了预测该地区2018年的环境基础设施投资额，建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据（时间变量t的值依次为1，2，…，17）建立模型①：=-30.4+13.5t;根据2010年至2016年的数据（时间变量t的值依次为1，2，…，7）建立模型②：y=99+17.5t.

（1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值;

（2）你认为用哪个模型得到的预测值更可靠？并说明理由.

评注 题11是基于真实情境的开放性问题，答案并不唯一.可以从图形（折线图趋势）视角，也可以从代数（计算结果）层面来判定模型②预测值更加可靠.题11赋予考生更大自主决策空间，鼓励考生多角度地独立解决问题，体现新高考命题的开放性与创新性. 3.6 考查分析和解决问题的综合能力

题12 （2018·新课标1卷理20）某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品.检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为p（0<p<1），且各件产品是否为不合格品相互独立.

（1）记20件产品中恰有2件不合格品的概率为f（p），求f（p）的最大值点p0;

（2）现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的p0作为p的值.已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用.

（ⅰ）若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为X，求EX;

（ⅱ）以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？

评注 题12与函数、导数等知识交汇，考查学科知识综合应用的力.需要考生构建函数关系式，运用导数作为工具来确定最大值点p0.可以预见未来这类试题出现的概率较大， 凸显中国高考评价体系中“四翼”明确提出的应用性与综合性.还必须指出的是，概率统计不等同于数学，教学中要重視培养统计意识.要求考生立足统计视角，借助数学工具来处理问题，这正是题12失分的主要原因，也是当年高考后对本题争论不休的缘由.

4 对2022年概率统计备考建议

4.1 重视核心概念，提升学生理解、辨析数学概念的根本能力

概念是数学的细胞，是思维的载体，是创新的源泉. 数学教学中最困难、最棘手的就是概念，因此学术界将数学概念誉为“冰冷的美丽”.概念教学是数学教学的核心环节，整个数学知识体系是建立在概念基础之上. 长期以来，数学教师重解题技巧，轻概念生成，追求概念教学最小化和习题讲解最大化，导致学生对概率统计基本概念死记硬背、机械记忆.章建跃指出，目前概念教学陷入“一个定义、二项注意、三个例题、N个强化训练题”怪圈，这与立德树人背道而驰，不利于核心素养的培养，制约学生能力发展，这是目前中学数学教育中最紧迫、最值得关注的课题.在概率统计复习中，针对核心概念（比如基本事件个数、条件概率、事件的独立性等）要舍得花时间与精力，既要采取“正面突破”，又要辅以“事后补救”等策略[2]，通过正面与反面经典案例来辨析概念，进而巩固概念、精致概念，悟透概念的本质[3].

4.2 重视阅读理解，提升学生在实际问题中抽象数学关系的建模能力

近年来，回归分析、残差分析等成为热点、重点、难点，并有逐年加大考查力度的趋势.这类试题文字篇幅较长、信息含量较大、符号图表密集、运算过程复杂、参考数据冗长、涉及公式较多.正如文[4]指出学生读不懂题意是造成概率统计试题失分的主要原因之一，因此加强阅读能力的培养是解决问题的关键.通过阅读发现和提出概率统计问题.利用数学知识解决实际问题，体现了数学的应用性.

4.3 重视决策表述，提升学生运用所学知识解决问题的综合能力

文[5]认为基于决策提供情境而命制的情境化试题，不仅能在应用性和综合性上考查“四层”的相关内容，还可以帮助学生通过相应的情境活动坚定数学的价值认同.比如，2017年全国Ⅰ卷理科20题概率统计与函数导数交汇、2019年全国Ⅰ卷理科概率与数列交汇、2021年全国新高考Ⅱ卷的概率与函数、方程交汇等，上述试题均对知识迁移提出较高要求.教学中要重视概率统计语言的准确阐述，感受统计意义和价值，培养学生的统计意识.再如，在投资收益类问题中，一般以期望作为决策的标准;在没有明确指明决策标准时，概率、期望和方差都可以作为决策依据.意味着答案可能不唯一，只要言之有理都可以得分.可以预计开放式试题在高考中出现的频率越来越多.

4.4 重视公式结论，提升学生在数字特征分析和应用中的推理能力

相比于旧版教材，新版教材对一些公式、结论给出较为详细的阐述.教师不仅要重视这些结论：E（X+Y）=E（X）+E（Y），D（X）=E（X2）-[E（X）]2，更要展示它们的推理论证过程：=∑ni=1（xi-）（yi-）∑ni=1（xi-）2=∑ni=1xiyi-n∑ni=1x2i-n2，以便考生得心应手、运用自如.

4.5 重视核心素养，提升学生在处理概率统计问题中的关键能力

统计是一门处理数据的科学.统计学是研究如何收集、整理、分析数据以及由数据分析结果作出科学决策.概率论是研究随机现象规律的科学.概率是一种度量，刻画随机事件发生可能性大小.在解决概率统计问题过程中，把实际问题抽象为数学问题，形成数学的研究对象（培养抽象素养）;通过逻辑论证，促进数学内部和谐的发展（培养逻辑素养）;通过构建模型，构建数学与现实世界的桥梁（培养建模素养）;通过图形、表格，将文字、图表、数据、参考公式等融为一体（培养直观素养）;通过优化计算，求得运算结果（培养运算素养）;通过数据分析，发现规律，作出决策（培养数据分析素养）.由此可知概率统计问题囊括六大核心素养，这正是彰显新高考导向下的命题理念的最佳素材.5 结束语

概率统计问题聚焦六大核心素养，是综合考查学生用数学眼光观察问题、用数学思维分析问题、用数学语言表达问题、用数学知识解决问题的有效途径，是全面落实立德树人、发展素质教育的重要载体，是优化思维品质、培养核心素养的经典范例，这也正是近年来概率统计试题成为高考热点、重点的缘由，更是逐年加大考查力度的依据.然而，必须承认概率统计是高中数学较为棘手的内容，这也是导致考生心理畏惧概率统计试题的因素.难怪概率统计学家Kapadia与Borovcnik感叹：“概率是一个难教又难学的内容……，在概率统计中，无论是其非常核心的部分，还是它的概念及其比较简单的应用，到处都有似是而非和违背直觉的说法.”教师要努力提升自身的业务水平与专业素养.正如文[6]警示：“通过调查研究以及收集的数据统计结果表明，纵使是处于金字塔顶部的重点高中数学教师，他们的概率统计知识储备严重不足，80%以上的教师对大部分概率统计基本概念的认识都处于模糊状态，理解深度不够，缺乏用这些概念答疑解惑的能力，影响概率统计知识的教学效果.”这就说明2022年及未来高考，一方面进一步加大概率统计考查力度，另一方面考查难度与力度依然是一个缓慢提升的过程.如同文[7]指出，在高三复习备考过程中，教师要重视回归教材、精致概念、强化阅读、落实细节、渗透思想、培养素养等下功夫，以不变应万变.

参考文献

[1] 王淼生.研究高考试题是倒逼教师提升专业素养的杠杆——以“2021年全国高考数学新高考Ⅰ第8题”为例[J] .中学数学杂志（高中），2022（01）：5256.

[2] 王淼生.概念：数学教学永恒主题[M] . 厦门：厦门大学出版社，2018.

[3] 王淼生.与其满腹困惑 不如求教专家[J] . 中小学数学（高中版），2021（12）：16.

[4] 任子朝，陈昂，赵轩.加强数学阅读能力的考查展现逻辑思维功底[J]. 数学通报，2018（06）：813.

[5] 柯躍海.高考数学试题情境的创设实践[J]. 中国考试，2020（06）：19.

[6] 李勇，章建跃，张淑梅，刘文慧.全国重点高中数学教师概率统计知识储备现状调查[J].数学通报，2016（09）：19.

[7] 王淼生.统计试题得分低的原因及应对策略——以“2020年福建省质检理科第20题”为例[J] .福建基础教育研究，2020（08）：6468.

作者简介 王淼生（1966—），男，正高级教师，特级教师，“苏步青数学教育奖”一等奖获得者，第六届全国教育科学研究优秀成果奖二等奖获得者，“福建省基础教学成果奖”特等奖获得者，中国数学奥林匹克高级教练，福建省高层次人才，厦门市拔尖人才，厦门市首届名师工作室领衔人，厦门市卓越教师，厦门市专家型教师，厦门市杰出教师.

周翔（1979—），男，高级教师，厦门市数学学科带头人，福建省第二届教学技能大赛一等奖获得者，厦门市中小学技能大赛一等奖获得者，厦门市课堂教学创新大赛一等奖获得者.