五法求解数列通项公式的思路例析

马应雄

(陕西省汉中市镇巴中学)

数列不仅在高中数学中占有不可或缺的地位,而且在高考中也有重要地位,求解数列的通项公式是经常考查的知识点,通项公式能够直接反映出数列的实质,是解答数列问题的关键所在.求解数列通项公式的题型多样,求解方法灵活多变,很多学生还未真正掌握求解通项公式的方法.本文将利用几个具有代表性的例题帮助学生理解和掌握求解数列通项公式的几种常用方法,希望能够帮助学生厘清思路,正确求解问题.

1 公式法

公式法是求解数列通项公式最简单、最基础的方法,主要利用等差数列或等比数列对应的公式求解,即an＝a1＋(n－1)d或an＝a1qn,适用于能直接解得数列的首项和公差(或公比)的题目.利用公式法求数列通项公式的具体步骤如下:1)根据具体题意确定数列的类型;2)分析数列的首项、公差或公比,并利用对应的公式计算,解得所求的数列通项公式.

2 累加法

累加法,也叫逐差叠加法,指的是多次相加求解的意思,其本质是恒等式an＝a1＋(a2－a1)＋(a3－a2)＋…＋(an－an－1),适用于差值不是相等就是有规律变化的情形.当给定条件最终可转化为形如an＋1＝an＋f(n)的形式时(f(n)可以是常数,也可以是等差数列或关于n的一次函数、分数函数等),便可利用累加法求解通项公式.利用累加法求通项公式的具体步骤如下:1)根据题意将已知条件转化为an＋1－an＝f(n)的形式;2)利用累加法,将各个等式等号左、右两边分别相加,计算解得通项公式;3)检验n＝1时上述通项公式是否成立,得到最终答案.

例2 若数列{an}满足an＋1＝an＋2n＋1,a1＝1,求数列{an}的通项公式.

分析 本题是一个典型的an＋1＝an＋f(n)型数列,将其整理成an＋1－an＝2n＋1的形式,直接利用累加法,解得an＝n2(n≥2),检验n＝1时上式也成立,确定an＝n2.

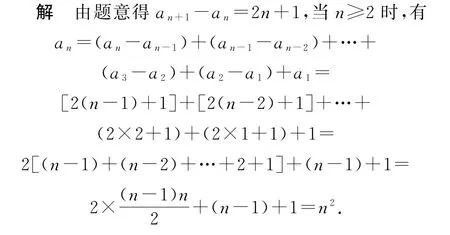
当n＝1时,a1＝1,也满足上式.因此,数列{an}的通项公式为an＝n2.

3 累乘法

4 递推作差法

递推作差法是根据递推公式采用逐项相减的方法求解问题,一般指的是利用公式Sn－Sn－1＝an求解数列的通项公式,适用于已知Sn与an的题目.利用递推作差法求通项公式的具体步骤如下:1)作差,将题设中的等式两两相减解得出当n≥2时的通项公式(Sn－Sn－1＝an)或公差;2)结合题意分析数列首项的值,进而解得数列的通项公式.

例4 (1)已知Sn表示数列{an}的前n项和,an＞0,且满足a2n＋2an＝4Sn＋3,求数列{an}的通项公式;

(2)已知数列{an}的前n项和为Sn＝n2－10n,求数列{an}的通项公式.

因为an＞0,所以an＋1－an＝2,当n＝1 时,由a21＋2a1＝4S1＋3,解得a1＝3或－1(舍).因此,数列{an}是首项为3,公差为2的等差数列.

综上,{an}的通项公式为an＝2n＋1.

(2)当n≥2 时,an＝Sn－Sn－1＝(n2－10n)－[(n－1)2－10(n－1)]＝2n－11.当n＝1 时,a1＝S1＝12－10×1＝－9,也满足an＝2n－11.因此,数列{an}的通项公式为an＝2n－11.

5 待定系数法

待定系数法是求解数列通项公式的常用方法,它是将一个多项式表示成含有待定系数的形式,进而得到一个恒等式,利用恒等式的性质得出系数应满足的方程或方程组,再求出待定系数或找出某些系数所满足的关系式.待定系数法适用于递推式为an＋1＝pan＋q(p≠1,pq≠0)或an＋1＝pan＋qn＋1(p,q为常数)等类型问题.利用待定系数法求通项公式的具体步骤如下:1)构造等比数列,根据具体问题构造形如an＋1＋x＝p(an＋x)的等式,解得x的值;2)代入x的值计算数列{an＋x}的通项公式,并借此解得所求数列的通项公式.

数学归纳法也是求解数列通项公式的常用方法,此方法对学生的能力要求较高,除此之外,还有一种简单的方法——观察法,即直接分析前几项数列的规律和特点,直接解得通项公式.