例讲高中数学新定义问题
李子修
(山东省寿光中学)
新定义问题在高考中经常出现,考查学生的知识迁移能力,是高考试卷中的一大亮点.很多学生遇到新定义问题往往不知如何下手,为增强学生自信,使其找到解答新定义问题的思路,有必要将新定义问题作为一个专题进行讲解.
1 集合新定义问题
集合是高中数学的基础知识.相关新定义的问题较为抽象,要想正确作答,不但需要深入理解、牢固掌握集合基础知识,而且需要根据题干创设的情境,充分考虑每一种满足题意的可能.
例1 已知集合I={1,2,3,4},A,B均是I的子集,若A∩B={1,3},则称(A,B)为一个“理想配集”,其中(A,B)和(B,A)是两个不同的“理想配集”,则满足条件的“理想配集”的个数为( ).
A.16 B.9 C.8 D.4

该问题的难度并不大,需根据“理想配集”的定义,对可能存在的情况进行分类讨论.
因为(A,B)和(B,A)是两个不同的“理想配集”,所以以A为研究对象进行分类讨论.
当集合A={1,3}时,则集合B可以为{1,3},{1,2,3},{1,3,4},{1,2,3,4},共4种结果;当集合A={1,2,3}时,则集合B可以为{1,3},{1,3,4},共2种结果;当集合A={1,3,4}时,则集合B可以为{1,3},{1,2,3},共2种结果;当A={1,2,3,4}时,则集合B可以为{1,3},共1种结果.
综上,满足条件的“理想配集”的个数为4+2+2+1=9种,选B.
2 函数新定义问题
函数是高中数学的重要知识点,相关新定义问题经常出现在测试以及高考中.解答该类问题的关键在于吃透新定义,建立新定义与所学知识之间的内在关联,对问题进行灵活转化,化陌生为熟悉.
例2 设f(x)在(a,b)上的导函数为f′(x),f′(x)的导函数为f″(x).若f″(x)<0在(a,b)上恒成立,则称函数f(x)在(a,b)上为“凸函数”.若f(x)=ex-xlnx-px2在(1,4)上为“凸函数”,则p的取值范围为_________.

3 数列新定义问题
数列是高中数学的难点,相关新定义问题有时会出现在高考中.解答数列新定义问题时应认真审题,认真分析新定义表示的含义,尤其当给出新的数列时应注重研究新数列的相关性质,提高数列性质的应用意识,以达到顺利解题的目的.


4 平面向量新定义问题
平面向量是高中数学的重要知识点,常作为解答其他问题的工具,但部分测试中会单独考查平面向量知识,尤其会在这部分设计新定义问题考查学生知识迁移的能力.解答平面向量新定义问题应注重联系平面向量的几何运算、坐标运算法则,对问题进行合理转化,以迅速找到解题的切入点.


解答该题需要充分理解新定义的含义.根据题干给出的条件建立相关的平面直角坐标系,运用数形结合法便可直观解答出满足条件的m的取值范围.

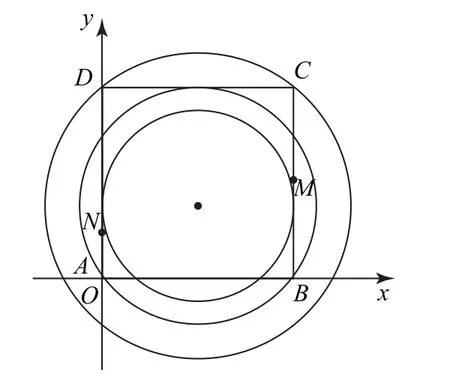
图1
5 小结
对高中数学新定义问题进行研究可知,这类问题往往给出新的定义,要求学生运用所学知识进行分析.为使学生掌握这类问题的解题思路,应注重与学生一起剖析相关例题,使其认真体会解题的具体过程,尤其要引导学生认真阅读题目,吃透题意,弄清楚题干中相关参数之间的联系,积极运用转化思想,化陌生为熟悉,实现问题的有效突破.

