动手实践 体验过程 生长能力

高亚健

[摘  要] 数学课堂教学是“教”与“学”双边活动，在实施以“动手实践”为主导的课堂教学中，教师可以通过精选操作内容与方法，把握操作时机，组织学生开展有序的操作实践活动，以建立出一种切实有效的教与学的模式，促进学生数学素养的提升. 文章从动手实践活动的视角，结合“特殊三角形”的复习课，谈谈如何提升探究活动的设计内涵，引发学生动手实践、体验过程、生长能力.

[关键词] 动手实践;特殊三角形;分类讨论

提出问题

优化教学方法，开放学生的创造潜能，将动手实践活动融入数学课堂是提高学生数学素养的有效途径. 一般情况下，教师习惯利用“练习+讲解”来勾画复习课，这样的方法呆板无趣，学生很难提起学习的兴趣. 在实施以“动手实践”为主导的课堂教学中，教师可以通过精选操作内容与方法，把握操作时机，组织学生开展有序的操作实践活动，以建立起一种切实有效的教与学的模式，促进学生数学素养的提升. 下面，笔者以“特殊三角形”的复习课为例，谈谈如何提升探究活动的设计内涵，引发学生在数学活动中动手实践、体验过程、生长能力.

课堂实录

1. 适切导入，引出课题

师：本节课我们主要来回味特殊三角形，那么你知道哪些特殊三角形呢？

生1：等腰三角形、等边三角形、直角三角形.

生2：等腰直角三角形.

师：你们罗列出的这四种特殊三角形，它们的特殊体现在哪里呢？

生3：等腰三角形的两条腰相等，两个底角也相等;等边三角形的三条边都相等;直角三角形有一个角是直角.

生4：等腰直角三角形有一个直角，且两直角边相等，两个底角是45°.

师：很好，根据刚才的总结，这些特殊三角形都是用什么来刻画的呢？

生5：边与角.

师：非常好，那这节课就让我们从边与角这两个角度和特殊三角形再来一次亲密接触吧！

设计意图 “温故而知新”，在开课之始，教师引领学生通过对旧知的回顾进行了一次良好的过渡，自然而然地引出了课题. 本节课中，教师通过罗列特殊三角形，给学生的思维提供了一个缓冲的空间，用以激起学生进一步探究的欲望. 这样看似普通的“温故而知新”的导入，为之后的探索指明了正确的方向.

2. 动手实践，获得体验

探究活动1：填一填.

（1）已知等腰三角形ABC的其中一内角是40°，则另外两个内角的度数分别是____和____. （师生共同探究，发现等腰三角形ABC的内角分为顶角和底角，进而得出两种结果：70°和70°，40°和100°）

（2）已知等腰三角形ABC的两条边的长度分别是4和5，则其周长为_____. （师生又一次共同探究，根据等腰三角形ABC的边可分为腰与底边，进而得出两种结果：13或14）

（3）已知Rt△ABC的两条边的长度分别是4和5，则其周长为____. （师生再次共同探究，根据Rt△ABC的边可分为直角边与斜边，进而得出两种结果：12或9+）

（4）根據以上各题，你有何体会或感悟？（通过归纳、总结和反思，学生领悟到在探求特殊三角形边或角时需要充分运用好分类讨论思想）

探究活动2：证一证.

如图1所示，已知△ABC中，AB=BC=4，AD为边BC的中线，AD=2，那么△ABC是什么三角形？并证明. （学生读题）

生6：△ABC是等边三角形. 证明如下：因为AB=BC=4，AD为边BC的中线，所以BD=BC=2. 在△ABD中，因为AB2=16，AD2+BD2=（2）2+22=16，所以AB2=AD2+BD2，所以△ABD为直角三角形，所以∠ADB=∠ADC=90°. 在△ADB与△ADC中，因为∠ADB=∠ADC，

AD=AD，

BD=DC，所以△ADB≌△ADC，所以△ABC是等边三角形.

生7：我也认为△ABC是等边三角形，不过我的证法和生6有些不同. 同生6一样证得△ABD为直角三角形，所以AD⊥BC. 因为BD=CD，所以AD垂直且平分BC，所以AB=AC，所以AB=AC=BC，所以△ABC是等边三角形.

生8：我也是同生6一样证得△ABD为直角三角形，因为BD=2，AB=4，根据“30°所对的直角边为斜边的一半”的逆定理，可得∠BAD=30°，所以∠B=60°，所以△ABC是等边三角形.

师：刚才三名同学的前一半证明都离不开“证明△ABD为直角三角形”，且三人运用的方法相同，都用到了什么定理？

生（齐）：勾股定理的逆定理.

师：此处还用到了哪些知识呢？（学生又一次开始总结提炼）

师：通过解决本题，你们又有何启示？

生9：多方位、多角度分析和思考一道相同的问题，往往可以得出多种不同的解法.

探究活动3：折一折.

（1）在日常生活中，我们可以折出一个等腰三角形吗？请拿出准备好的白纸试一试，能不能折出一个等腰三角形？（师生一起操作，不仅折出了一般的等腰三角形，还折出了等腰直角三角形和等边三角形）

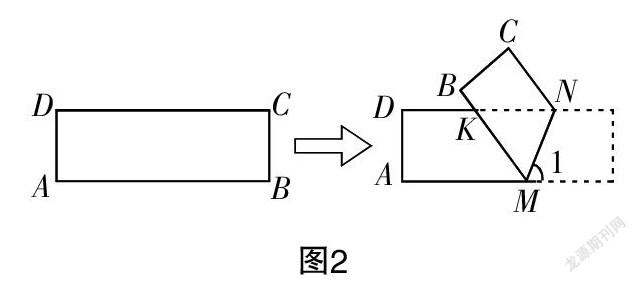
（2）如图2所示，已知四边形ABCD为一张长方形纸片，且AD=BC=，AB=CD=5，分别在边AB，CD上取点M，N，将纸片沿着MN折叠，使得MB交DN于点K，并得出△MNK.

①那么△MNK是等腰三角形吗？若是，请证明;若不是，请说明理由.

②如果△MNK是一个等边三角形，试求出折痕MN的长.

③如果△MNK是一个直角三角形，试求出折痕MN的长，并求出△MNK的面积.

探究活动4：画一画.

如图3所示，若将一张直角三角形纸片放置在平面直角坐标系中，且直角顶点与坐标原点重合，一直角边OB落在y轴上，OA=8，OB=6.

（1）求AB.

（2）若x轴上有一点P，使得△PAB为等腰三角形，这样的点P有几个，试求出点P的坐标.

探究活动5：拼一拼.

（1）如图4所示，已知花园里有一个Rt△OAB花圃，若想将其改造成一个等腰三角形花圃，且扩充部分是以OA为直角边的直角三角形（与原三角形不重叠），试求出改造后的等腰三角形花圃的周长.

（2）若将“以OA为直角边的直角三角形”换为“与Rt△ABO有一条公共边的直角三角形”，结果又如何？

设计意图 学生的数学思维在很多情况下不是主动发生的. 本环节中，教师以有效问题作为引导，为学生设计了与教学内容相关的动手实践活动，让学生在观察、操作、探究等实践活动中触动思维，获得体验.

3. 总结反思，生长能力

师：通过今天的学习，你有何收获？

生10：在今天的复习中，我知道了分类讨论是一种重要的思想方法.

生11：倘若我们能多角度、多方位地观察和分析问题，则可以发现一道习题的多种不同的解法.

生12：通过对边与角的分析，让我重新认识了特殊三角形，并懂得了它的特殊之处有……

设计意图 教师在教学中要尽量为学生提供反思的机会，可以培养学生的反思品质，可以为后续学习积淀经验与方法. 这一环节中，教师让学生从自身的认识出发谈谈感悟与体验，学生基于自身的操作体验进行了阐述，促进了思维的拔节生长.

几点感悟

1. 在实践操作中大胆猜想，强化感性认识

猜想是学生初步感知事物后进行的判断，这一过程对于学生获取知识来说十分重要，因此在动手实践中要鼓励学生大胆猜想. 例如，当教师抛出问题“在日常生活中，我们可以折出一个等腰三角形吗”，学生很笃定地猜想到“可以”. 此时学生就会跃跃欲试地去验证自身的猜想是否正确. 这样一来，利用好动手操作得到各种等腰三角形也就水到渠成了. 在这个过程中，学生的动手操作能力和空间感知能力得到了锻炼与提升，他们的感性认识也得到了强化.

2. 有机融合操作与思考，促进理性思维

动手操作的活动离不开数学思维的参与，思维参与的深度不同，教学的效果也会有所不同. 本节课中，教师设计的每个探究活动并非简单地模仿操作，而是让学生经历由浅入深的探究过程，实现了操作与思维的有机融合，促进理性思维的生长. 探究活动中，教师从学生的认知规律出发自主创新设计，并注意到挖掘知识生长点和知识延伸点，进一步探究活动的目的，让学生感受探究的乐趣和收获的喜悦，体悟蕴含的数学思想方法. 对特殊三角形的理解经历从“朦胧”到“觉醒”，最后走向“清晰”，使得学生对特殊三角形相关知识的理解逐步走向深刻，并获得数学探究的成功体验.

3. 有度渗透数学思想，促进思维品质的形成

数学思想是思维的核心，在动手操作的过程中，不失时机地渗透数学思想，可以通过探索、感知与体验，养成良好的思维品质. 例如，探究活动“画一画”可以让学生在操作中自然领悟隐含在数学探究中的分类讨论思想，并形成自然应用的意识. 正是因为在探究中对分类讨论的充分理解和应用，才讓学生从量的积累到质的提升，从而自然应用到今后的问题解决中去.

总之，采用这种动手实践、体验过程、生长能力的创新实践教学方法，能充分调动学生学习数学的积极性，让学生在手、口、脑等协同合作下感受到数学的魅力，充分感受到数学思想方法的生长，发展自身的创新潜能，让复习课从枯燥、乏味、低效的窘境中走出来，变得有趣、有味，这不失为数学探究性教学的上策.