聚焦知识关联 挖掘章始魅力

丁伯军

[摘  要] 知识，是教师进步与学生成长所依托的精神食粮，将知识通过有效的途径传授给学生，让学生能够高效吸取是每个教师的使命. 诚然，知识并不是孤立的，碎片化的教学无法达到预期的效果，知识的完整性已成为新时期教学必须遵守的原则. 在初中数学教学中，章节起始课作为每章节内容教学的开始，担负着承接新旧知识及统领章节内容的重任，在教学中有着举足轻重的作用，所以探讨其有效的教学途径一直是一线教师及教育专家热议的话题.

[关键词] 初中数学;起始课;魅力;策略

笔者多年从事初中数学教学工作，对章节起始课的有效教学进行了多次思考及尝试. 在不断反思与改进中越来越深刻地认识到，章节起始课的魅力在于“承上启下”，它能将不同的知识串联成完整的板块，益于学生知识进步及能力发展. 从整体的视角设计教学方案，采用知识整合及资源重组的方法实施教学方案，让章节起始课涉猎的知识更多、更广，可以高效发挥它的价值. 下文笔者结合教学实际，从内容、方法、体系、视角四个方面谈谈自己的认识.

内容关联：知识迁移

内容关联是指数学知识内容层面的相互关联或某个知识板块的多角度联系，它是数学知识之间最明显的联系. 在章节起始课教学中，关注知识内容的关联可以让学生经历知识的迁移过程，体悟知识的前后联系，促进知识的完整建构.

以“6.1 平方根”（人教版七年级下册）为例，笔者设计了如下的教学环节：

投影：22，32，42，….

问题1：这种运算你学过吗？是什么运算？

问题2：在22中，两个“2”分别代表什么？它们的运算结果叫什么？

师生共同归纳并板书： （底数）指数=？（  ）指数=幂;（底数）？=幂.

追问：它们分别是什么运算？对于“底数、指数、幂”这三个元素，可以“知一求二”吗？

设计意图 以最简单的运算开始研究，可以降低学生学习的难度，让学生树立起学好本节课内容的信心;同时，由学生熟悉的乘方引入开方的概念，一方面利于学生接受，另一方面可以让学生明晰乘方与开方的联系，学会知识迁移;另外，在概念教学中渗透高中阶段的对数运算，利于学生知识拓展，助推学生高阶思维的发展.

方法关联：发展能力

方法关联是指在数学教学中利用相同或类似的方法学习一类知识或研究一类问题，它是发展学生学习能力的有效途径. 数学是一门注重方法的学科，方法的习得可以助推能力的发展，因此方法的领悟在某种程度上比知识的掌握更加重要.

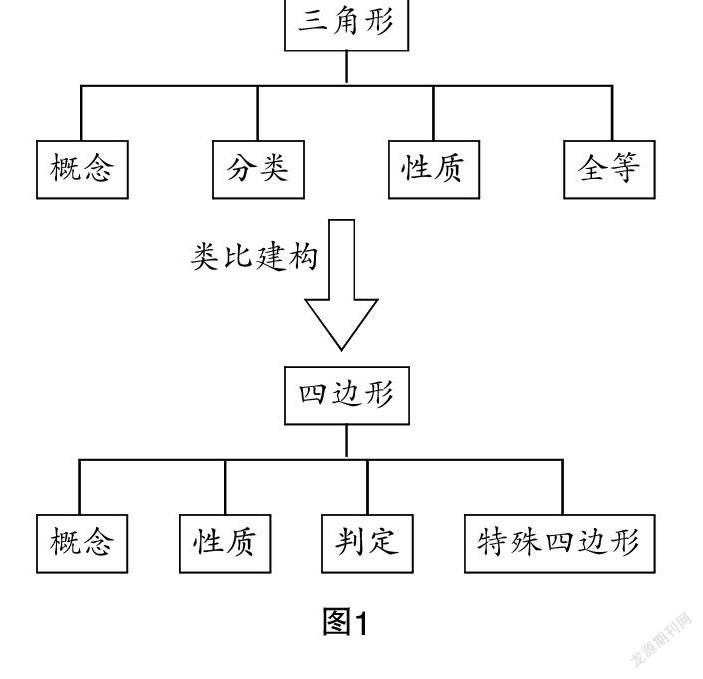
在“18.1 平行四边形”（人教版八年级下册）的教学中，让学生类比学习三角形所采用的方法，思考四边形的学习可采用的方法，完成一次类比建构. 图1即知识结构图：

设计意图 从三角形的知识框架出发，猜想平行四边形的探究方法，让学生找准本章节的学习方向，明确学习目的，学会类比方法;同时，三角形与四边形是初中几何的重点，整体建构可以让学生发现它们之间的联系，体悟到知识的完整性;另外，采用知识结构图的形式可以将本章节的知识内容整体呈现，起到了统领的作用，为展开本章节的教学做好铺垫.

体系关联：催化认知

体系关联是指相关内容来源于同一知识体系或最终服务于同一目标领域，是数学知识之间的深层次关联. 在讲授知识的同时渗透知识体系的内涵，可以激发学生的高阶思维，催化学生对数学的深层认知.

例如，人教版七年级上册学生初步认识了几何图形中的点、线、面、体、边、角等元素，下册由相交线与平行线的研究正式展开初中几何的学习. 以下是章节起始课“5.1 相交线”的教学片段：

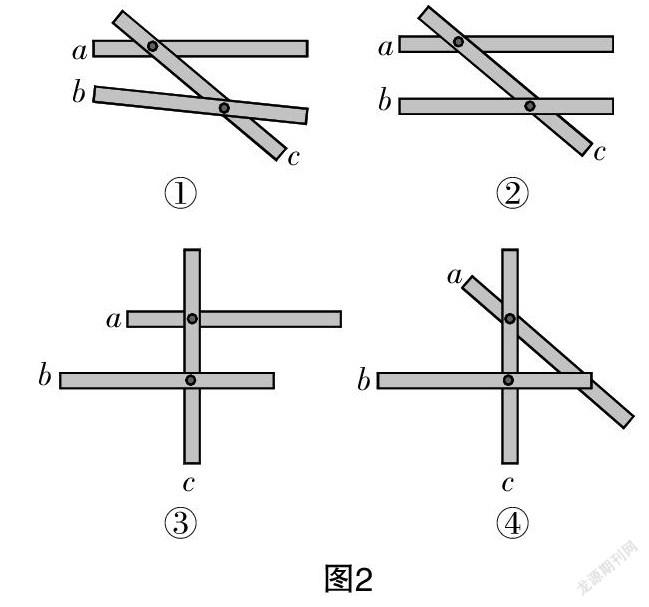
思考：如图2所示，将三根木条a，b，c按照图①的方式钉在一起，木条可以绕着两颗钉子转动，现在将它们想象成在同一平面内可以向两端无限延伸的三条直线，观察木条在转动的过程中三条直线的位置关系会发生怎样的变化.

生1：直线c与直线a、直线c与直线b始终是相交的. 直线a与直线b有时相交，有时不相交.

师：不相交的两条直线我们称为什么位置关系呢？

生2：平行.

教师演示图②并板书“平行”的文字语言及符号语言.

生3：直线c与直线a、直线c与直线b虽然始终相交，但是它们还存在一种特殊的相交关系——垂直.

师：非常好，你的思维真严密.

教师根据学生的描述变换出图③并板书“垂直”的文字语言及符号语言.

师（追问）：如果直线c、直线a、直线b两两相交（如图④所示），这时三条直线能夠围成一个封闭的图形，这个图形是什么？

生（齐声回答）：三角形.

师：没错，在几何学习中，“线”是构成“形”的基本元素，我们研究的“线”最终都是为“形”乃至“体”做铺垫. 本节课我们将从线线关系开始展开讨论.

设计意图 由木条的转动移植到同一平面内两条直线不同的位置关系，是由具体到抽象的自然过渡，利于学生接受;教师通过模具演示但不强行灌输概念，让学生通过观察自己得出结论，体现教学以学生为中心的原则;对于学生的回答，教师不断给予肯定及引导，让学生自己摸索并深入思考，符合知识的生长规律;渗透“线”“形”“体”的关系，让学生明晰几何之间的整体关联，掌握本节课知识内容的同时对后续的知识内容产生期待，利于知识的整体建构.

视角关联：提高素养

视角关联是指在数学学习中思考、研究某一数学领域的基本视角或基本框架之间存在的内在联系，与体系关联相比，属于更高层次的思维水平. 在追求知识关联的数学章节起始课中，引导学生从视角关联的角度看待数学知识，利于数学核心素养的提高.

如下是笔者在执教“22.1 二次函数”（人教版九年级上册）时的引入环节：

问题1 为增加校园绿化面积，我校后勤部准备在教学楼后面的一块空地上围出一块矩形花坛用于种植花草. 如果计划用20米的篱笆围出一块矩形花坛，并且让花坛一面靠墙（墙的长度足够），当矩形的长与宽是多少米时，其面积恰好是18立方米？

答 设矩形的一边长为x米，则（20-2x）x=18.

问题2 用20米的篱笆靠墙围出一块矩形花坛（墙的长度足够），当矩形的长与宽是多少米时，其面积最大？

答 设矩形的一边长为x米，面积为y平方米，则y=（20-2x）x.

问题3 用20米的篱笆靠墙围出一块矩形花坛，如果墙的长度为8米，那么当矩形的长与宽是多少米时，其面积最大？

答 设矩形的一边长为x米，面积为y平方米，则y=（20-2x）x（6≤x<10）.

思考 （1）我们是否遇到了一个之前没有学过的函数？与一次函数相比，这个新函数有什么不一样？

（2）回忆一次函数的性质，猜想一下二次函数有哪些性质.

（3）与一次函数相比，这个新函数的图像会是什么样子的？

（4）这个函数与一元二次方程相似，它们之间会有什么联系呢？

（5）你还能找到我们学过的与之有联系的内容吗？

设计意图 首先，由简单的实际问题作为切入点，逐步增加条件，使问题有梯度，符合学生的认知规律;其次，让学生认识到，这三个问题涉及了一元二次方程、二次函數的概念、二次函数的最值三个方面，引入二次函数时让学生领会到数学知识之间的内在关联;再次，在学生接受了新函数后引导学生发现二次函数与一元二次方程的关系，并学会从二次三项式的视角分析相应的问题，促进数学抽象、逻辑推理等素养的发展;最后，由一元二次方程与二次函数的关系联想到即将学习的一元二次不等式的解法，这是知识的拓展与思维的延伸.

从知识整合的角度实施章节起始课的教学，最大的价值在于起到提纲挈领的作用，可以将零散的知识串联成串，扩大了知识的广度，增加了学习的深度，让学生学会学习、学会思考，真正体现了“知其然并知其所以然”的实质. 这不仅对学生现在，而且对他们将来甚至终生的学习都有着积极的作用. 数学知识犹如一颗颗珍珠，它们孤立存在时明亮却并不夺目，教师要做一个有心人，将这些珍珠整合串联成美丽的项链，让它们在一起散发出璀璨的光芒.