好问题驱动好课堂
翁海芳
[摘 要] 创新作为数学学科最根本的核心素养,主要表现在能不能提出有质量的问题上. 现结合一堂“图形和坐标”复习课实例,探讨如何实现问题驱动课堂教学,从而让学生既增长知识,又在创新能力上有所深化.
[关键词] 初中数学;问题驱动;课堂教学
创新意识和创新能力是数学学科最根本的核心素养,而创新意识和创新能力主要表现在能不能“提出问题—提出好问题—提出有价值的问题—提出能够推动数学发展的问题”上. 在我区的一次教研活动中,一位年轻教师展示了一堂“图形与坐标”(浙教版八年级上册第四章)复习课,整节课的问题由学生提出,提出的问题也由学生解决. 问题驱动、活动推动、情思涌动,让课堂精彩不断,课后学生意犹未尽,听课教师也深受感染. 笔者现将课例展现如下,与同行共同研讨.
教学实录
师:图形是几何范畴的,坐标是代数范畴的,联系这两者的载体是平面直角坐标系. 这节课我们就从最简单的几何图形“点”出发,共同回顾“图形与坐标”这章内容.
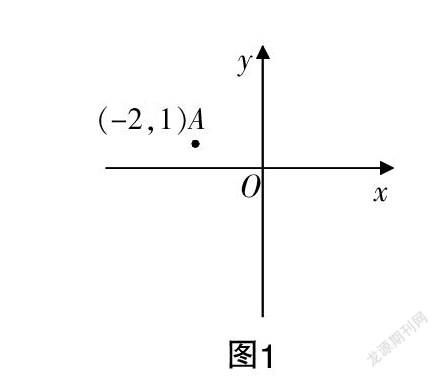
环节1 如图1所示,在平面直角坐标系中,已知点A的坐标为(-2,1),请问你能提出哪些数学问题?(要求问题简洁,考查的知识点不要重复,不能在问题中增加其他的点)
生1:点A在第几象限?(每个象限点的符号都有什么特征?)
生2:点A到x轴的距离是多少?(到y轴的距离呢?)
生3:點A关于x轴的对称点是什么?(关于对称点,我们总结出来的规律是什么?)
生4:点A关于一三象限角平分线的对称点是什么?
生5:点A向下平移三个单位得到的点的坐标是什么?(平移的规律是什么?)
学生提出了前面的问题,教师顺势补充了后面(括号里)的问题. 通过第一环节的追问,本章的知识点在学生的脑海里逐步呈现了,唤醒了学生的思维.
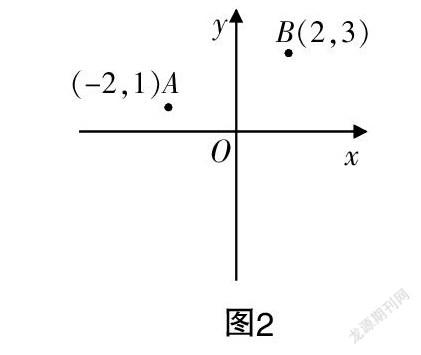
环节2 如图2所示,我们从一点出发提出了有关点的位置问题(静态的)和有关点的变换问题(动态的),现在增加一个点B(2,3),你又能提出哪些问题?
生6:求线段AB的长度. (构造直角三角形,利用勾股定理求解)
生7:求线段AB的中点坐标.
……
通过环节2的问题的提出和解决,点燃了学生的思维.
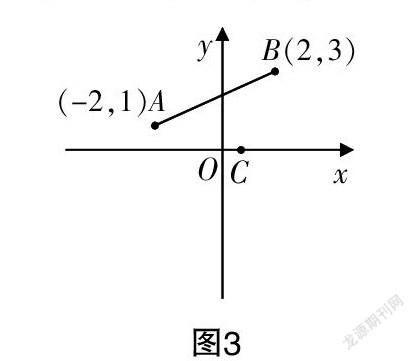
环节3 两点确定一条线段后,我们可以解决线段的长度和中点坐标的问题,如图3所示,如果再增加一个点C(a,0),你又能提出哪些问题?
师:这个点C和A,B相比有什么区别?(动点和定点),点C在哪里动?(x轴上)
生8:当△ABC的面积为5时,求a的值.
生9:当△ABC为等腰三角形时,求a的值.
生10:当△ABC是直角三角形时,求a的值.
生11:当△ABC的周长最小时,求a的值.
整堂课在学生不断提问和解答的过程中气氛高涨,最后进入了环节4.
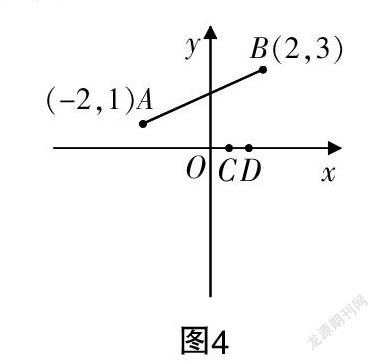
环节4 如图4所示,当平面直角坐标系中有三个点时,同学们就提出了很多有关三角形的问题——有关形状的、面积的、周长的,现在再增加一个点D(a+1,0),你还能提出什么问题呢?
生12:求四边形ABCD周长的最小值!
师:这个问题难度较大,它出现在近几年的中考压轴题中,因为时间关系,这个问题就留给大家课后思考吧!
教学点评
纵观整节课的教学设计,环节1给出了一个平面直角坐标系和一个点A,让学生回顾此章的基础知识:点的坐标在每个象限内的特征;点到x轴、y轴的距离;点关于x轴、y轴对称点的特征;点的平移规律等基本知识点. 环节2增加了一个点,在平面直角坐标系中已知两点,学生自然就想到了求线段长度以及求线段中点坐标等问题. 在教师的引导下,师生共同推导了相关的公式. 环节3又增加了一个动点C,学生自然地想到求最小值的问题. 由于三个点可能组成三角形,就特殊三角形提出了问题. 环节4再增加了一个点D,把本节课推向了高潮. 学生的情绪高涨,提出的问题是“求四边形ABCD周长的最小值”,此时教师点拨:“只要求出AC+BD的最小值,就可以求四边形ABCD周长的最小值.” 由于时间关系,将本问题放在课后让学生自主探索. 而这类问题,在近几年的中考压轴题中经常出现.
本堂课从最基本的点出发,延伸到线,拓展到面,从零散的知识演变,生成中考压轴题考查的内容,环环相扣,层层递进,浑然一体. 复习课不再是知识的再现,不再是要点的罗列,不再是解题技巧的灌输,而是通过学生的自主提问,把整章需要复习的知识要点都融入了进来,学生弄清了知识发生的来龙去脉,形成了重要的结论和解决问题的方法,并且思维始终处于积极的状态,圆满地实现了一堂高效复习课的目标. 为什么本节课能够实现以学生提出的问题推动整堂课的步步深入?主要是做好了以下三点:
1. 巧妙的预设让课堂有声有色
整节课教师只出示了四个点,但这四个点坐标的设置,教师之前是经过深思熟虑的. 第一个点(点A)在第二象限;第二个点(点B)与第一个点的横坐标互为相反数,落在第一象限;第三个点(点C)是x轴上的动点. 这样的安排给学生留足了空间,学生可以充分发挥自己的想象,通过旧知回顾,提出了有一定深度的问题. 当时听课的教师既惊讶学生能够提出这么多好问题,又感叹执教教师胆子真大,在公开课上也会如此冒险,潜台词是“万一学生提出的问题太难,课堂上解决不了怎么办”. 据笔者事后了解,本堂课之所以如此流畅,不是因为师生课前经过排练上了一堂表演课,而是因为教师基于学情作出了科学安排:学生在前学段已经学习了直角三角形、等腰三角形等特殊三角形的知识,但还没有学习相似、一次函数等内容;在平时的课堂上,学生初步感受过把几何图形放在平面直角坐标系中去解决,但没有深入. 教师认为学生会基于本章的知识点当堂提出问题,即使结合前面所学的特殊三角形,也能做到由学生提出、由学生解决. 一般不会出现漫无边际、束手无策、无法达到复习目标这样的极端情况. 教师通过巧妙的预设为学生搭台,以学生为主体的课堂最终呈现出了“百花齐放,青胜于蓝”的效果.
2. 合理的引导让课堂有边有界
课堂演变中,当教师给出了点A的坐标(-2,1)时,有学生提出了“求线段AO的长”这一问题. 教师马上引导,让学生注意到“不能在问题中增加其他的点”这一条件,还让学生注意到“要區分静止的点和运动的点”两种情况. 学生也就领会到“原来求线段长的问题我们暂时还不能提”. 如果点A是一个静止的点,就往坐标特征方面进行探索;如果点A是一个动点,就向轴对称变换和平移变换方面进行探索. 在环节3中,有学生提出了“当△ABC是等腰三角形时,求点C的坐标”这一问题,教师马上表扬了这个学生,并及时引导其他学生思考:“除了等腰三角形外,还有哪些特殊三角形?”学生就向直角三角形等方向进行了拓展,一步步推动思维走向深入. 整节课中,教师随时关注着学生的信息,在一些关键的节点给予引导或点拨,既提高了课堂的教学效率,又把握了引导的尺度,真正让每位学生站在了研究者的角度深入其境,感受到了学习的乐趣.
3. 华丽的转身让课堂有质有量
本节课做到了四个转身:一是教的转身. 教师的角色从知识的传授者转变为了学生学习的组织者、引导者、合作者,在课堂上除了认真聆听学生提出的问题外,还适时引导学生解决这些问题. 二是学的转身. 学生的角色从“学会”转变为了“会学”,“跟老师学”转变为了“自主学”. 学生不是停留在学会课本知识的层面上,而是站在研究者的角度深入其境;不是简单地“学”数学,而是深层次地探究以前学过的知识来提出高质量的问题. 三是课堂氛围的转身. 过程以“流畅、开放、合作、‘隐’导”为基本特征,教师尽可能减少对学生思维活动的干预,教学过程呈现了一种比较流畅的特征,整个情境以学生与学生、学生与教师之间的“对话”“讨论”为出发点,以互助、合作为手段,以提出问题、解决问题为目的,让学生在一个较宽松的环境中自主选择获得成功的方向,判断发现的价值. 四是评价的转身. 教师对学生的评价没有停留在学习结果的关注上,而是更加关注学生提出问题的过程,从而培养学生学习的兴趣,帮助学生认识自我,获得广泛的数学经验.
教学感悟
(1)问题驱动教学是一个不断“生长”问题和解决问题的过程,起于问题的开发,终于问题的解决. 驱动学生积极主动地参与学习的全过程,得到提出问题、分析问题、解决问题的能力,从而促进学生全面发展,发展和挖掘学生的各种潜力,激发学生思考,学会终身学习的本领. 教学中充分尊重和发挥学生的主体地位和作用,增加学生的主观能动性和合作精神,促进思维的发展,使学生真正成为学习的主人;而教师作为教学活动的参与者、管理者和调控者,与学生构成互动、互助、互相启发的态势,以驱动整个学习活动顺利完成.
(2)问题驱动教学对教师提出了更高的要求,教师不仅要知识渊博,还要具备洞悉学生心理、思维特点的能力,更要有灵活驾驭课堂教学的能力,能组织好课堂教学,促进学生提高问题意识和探索能力. 关键还要把握好四个“度”:把握好问题的难度,设计的问题要控制在学生认知的最近发展区;把握好问题的梯度,让学生如上楼梯一般在不知不觉中向高处登攀;把握好问题的密度,让课堂提问“四两拨千斤”,发挥最好的效果;把握好问题的角度,多个角度设计问题,培养学生的核心素养.
(3)问题驱动教学并非仅是教师设计问题、提出问题,学生解决问题,还包括学生发现问题、提出问题,由此来启发学生的创造性思维,提高他们的创新能力,完成一个“学生质疑—教师参与解疑—学生释疑”的完整过程,这是我们今后努力的方向.

