闭门器液压阻尼元件的特性仿真及试验*
杨礼康,戴光毅,宁晓斌,徐泽钧
(1.浙江科技学院 机械与能源工程学院,浙江 杭州 310012;2.浙江工业大学 机械工程学院,浙江 杭州 310014)
0 引 言
闭门器是一种安装在门头上,以保证门在开启后可以准确、及时地回到初始位置的装置。目前,市场上闭门器种类众多,如机械液压式闭门器、电动闭门器、电磁门吸式闭门器等。其中,因其完善的国家标准,机械液压式闭门器得到了广泛应用[1]。
液压闭门器的关键液压元件是柱塞、壳体及壳体上的阻尼孔件。闭门器柱塞和壳体相对运动时产生阻尼力,对闭门器复位起到缓冲作用,使门能以适当的速度及时、准确地回到初始位置[2]。
此前,有很多国内外学者对液压阻尼元件及其缓冲性能进行了分析。汪云峰等人[3]采用MATLAB和AMESim联合仿真的方式,对液压阻尼元件的主要结构参数进行了优化研究。梁翠萍[4]采用Fluent对缓冲过程中液压阻尼元件的内部流场进行了研究。王成文[5]采用Fluent软件对液压阻尼元件的阻尼结构进行了优化设计。李仕生等人[6]从工作原理角度出发,对液压阻尼元件的液压阻尼性能进行了分析,并建立了阻尼元件的油液流动模型。DUYM S等人[7,8]研究了液压阻尼元件在缓冲过程中的热传导规律,并在此基础上,对液压阻尼元件的建模提出了新的思路。GUNTUR R R等人[9]采用非线性建模的方式,对结构不一样的液压缓冲器进行了建模。CHANDAR N等人[10]采用仿真和试验并行的方式,对不同结构的液压缓冲装置进行了建模。
目前,国内外学者对液压阻尼缓冲进行了研究,并已取得了很多成果。但这些研究主要集中于缓冲器,很少有针对液压闭门器的系统研究。而企业在生产闭门器时,其设计参数往往要根据经验来选取,缺乏理论依据,因此无法保证产品质量和其工作性能。
因此,为分析液压闭门器的阻尼特性,笔者以某型号闭门器为研究对象,利用流体力学相关理论,简化闭门器结构,建立其液阻模型,并进而推导出闭门器柱塞复位过程的数学模型,通过Fluent流场仿真确认闭门器内部流道的压力分布,并将其与试验台的试验进行数据对比,以验证仿真模型的准确性,为闭门器的结构优化提供依据。
1 闭门器结构与液压油流动理论
1.1 液压闭门器结构和原理
该型号的液压闭门器结构如图1所示。
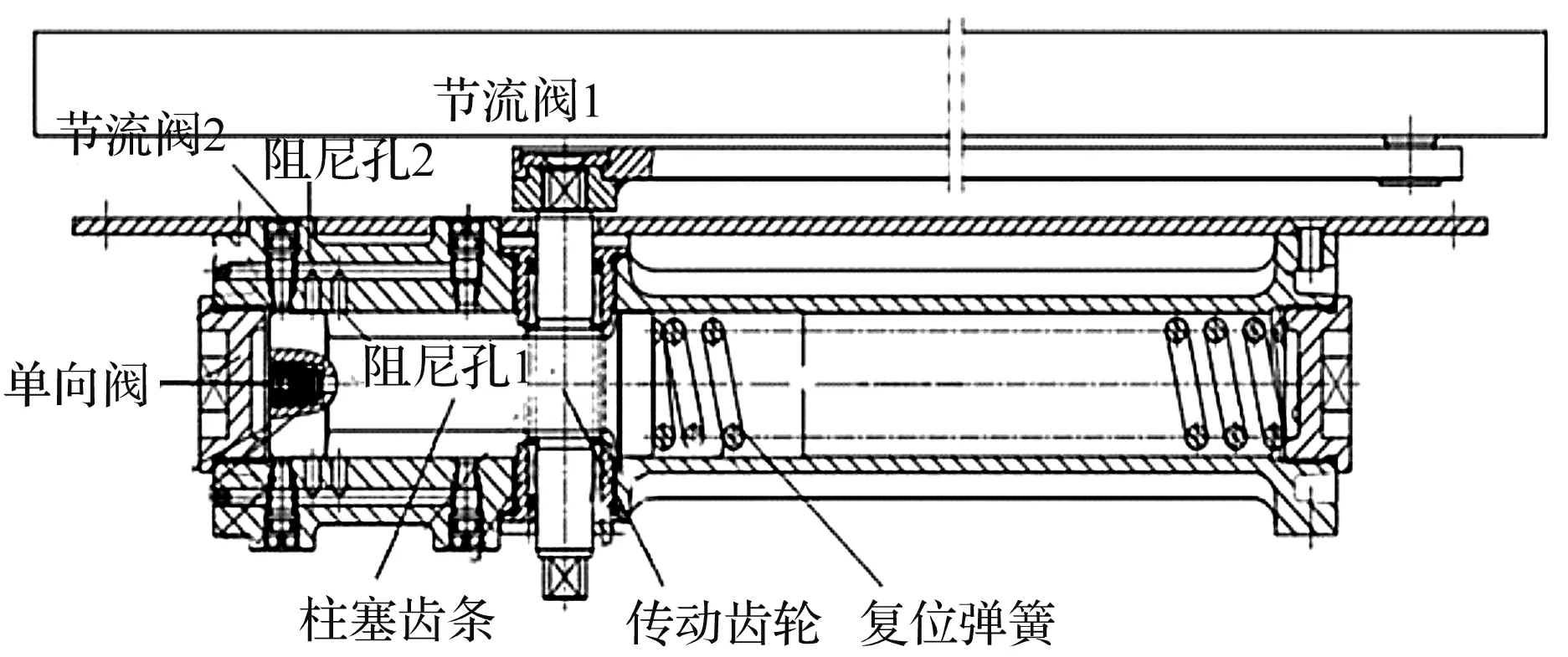
图1 闭门器结构图
图1中,闭门器的壳体固定在门扇上并通过连杆和门框相连;安装后向下的两个节流阀处于关闭状态,油液通过向上的两个阻尼孔和两个节流阀在闭门器内部流动。
(1)开门时,门扇带动连杆转动,传动齿轮随连杆转动一定角度,并通过齿轮齿条机构驱动柱塞齿轴向右方移动。在该过程中复位弹簧以及右腔的油液被压缩,右腔油压增大使得柱塞处的单向阀开启,右腔的液压油通过单向阀流到闭门器左腔中;
(2)关门时复位弹簧在开门过程中积蓄的弹性势能被释放,弹簧复原推动齿条柱塞向左移动,柱塞带动传动齿轮和连杆转动,使门关闭。在关门过程中,闭门器左腔的油压增大,单向阀处于关闭状态,液压油只能通过阻尼孔和节流阀流回右腔,该过程中形成的液压阻尼对弹簧复原构成了阻力,即通过节流实现缓冲的效果[11]。研究人员可以通过调节节流阀开度实现对不同行程段关门速度的控制。
针对上述闭门器工作原理,在闭门器复位过程中柱塞齿条运动至不同位置时,笔者建立其所受阻尼力的数学模型。
1.2 液体流经小孔及缝隙的流量
闭门器复位时,弹簧推动柱塞的表达式为:
q=Ap×vp
(1)
式中:q—流经阀孔的总流量,m3/s;Ap—活塞截面积,m2;vp—活塞运动的速度,m/s。
根据液压流体力学理论[12],按小孔类型的不同,液体流经小孔时的流量可分为3种情况,即薄壁小孔、细长孔和短孔。
笔者研究的闭门器其阻尼孔的通流深度l与孔径d之比满足0.5 (2) 式中:q—流经短孔的流量,m3/s;Cq—流量系数,在阻尼力计算中通常取0.62~0.63;At—阻尼孔截面积,m2;Δp—阻尼孔两端压差,MPa;ρ—液压油密度,kg/m3。 闭门器节流阀缝隙为带有一定锥度的环形缝隙,由于通过缝隙的流量较小,此处可简化为环形平面缝隙。 流经缝隙的流量为[13]: (3) 式中:h—阀芯和阀体之间的缝隙宽度,m;μ—油液动力黏度,Pa·s;d—阀芯直径,m;Δp—截流缝隙两端压差,MPa; 门在自动闭合的过程中,根据闭门器内部柱塞的位置主要可分为3个阶段: (1)柱塞位于阻尼孔1和节流阀1之间,此时油液从节流阀2和阻尼孔1,2流出柱塞左腔,再从节流阀1流回柱塞右腔; (2)柱塞位于阻尼孔1处,此时阻尼孔1被柱塞堵住油液从节流阀2和阻尼孔2流入管道,再从节流阀1流回柱塞腔; (3)活塞运动至两阻尼孔处,此时两阻尼孔均被柱塞堵住,油液从节流阀2流入管道,再从节流阀1流回柱塞腔。 笔者分别分析这3种状况下柱塞截面所受压力和柱塞运动速度的关系,由此分析在各种关门速度下柱塞所受阻尼力。 闭门器建模过程中,所需的参数主要分为两类:(1)结构参数,如阻尼孔的直径等(可以通过对实物的测量得到);(2)特性参数,如液压油密度等(可以通过查阅资料或根据厂家提供的参数获得)。其中,油液密度ρ=870.6 kg/m3,油液动力黏度μ=0.025 Pa·s。 闭门器液压元件参数如表1所示。 表1 闭门器液压元件参数值 当柱塞位于阻尼孔1和节流阀1之间时,此时的柱塞位置如图2所示。 图2 柱塞运动位置示意图1 油液从节流阀2和阻尼孔1、2流入管道,再从节流阀1流回柱塞腔,流出和流入柱塞腔的油液流量相等,即: (4) (5) q=ApVp (6) 以上三式联立,可得齿轴在此位置段时的速度与阻尼力的关系: (7) 式中:h1—节流阀1阀芯与阀套之间的缝隙高度,m;h2—节流阀2阀芯与阀套之间的缝隙高度,m;d—阀芯直径,m; 采用MATLAB辅助计算,笔者得到了该位置段时柱塞速度与所受压力的关系曲线,如图3所示。 图3 柱塞速度与所受压力关系曲线1 此时的柱塞位置如图4所示。 图4 柱塞运动位置示意图2 阻尼孔1被柱塞堵住,油液从节流阀2和阻尼孔2流入管道,再从节流阀1流回柱塞腔,流出和流入柱塞腔的油液流量相等,即: (8) (9) q=ApVp (10) 以上三式联立,可得齿轴在该位置段时的速度与阻尼力的关系: (11) 利用MATLAB辅助计算,笔者得到该位置段时柱塞速度与所受压力的关系曲线,如图5所示。 图5 柱塞速度与所受压力关系曲线2 此时的柱塞位置如图6所示。 图6 柱塞运动位置示意图3 油液从节流阀2流入管道,再从节流阀1流回柱塞腔,流出和流入柱塞腔的油液流量相等,即: (12) (13) q=ApVp (14) 以上三式联立,可得齿轴在该位置段时的速度与阻尼力的关系: (15) 利用MATLAB辅助计算,笔者得到该位置段时柱塞速度与所受压力的关系曲线,如图7所示。 图7 柱塞速度与所受压力关系曲线3 采用Fluent软件,笔者建立闭门器内部流道模型[14],并在柱塞运动至不同位置时,基于流场仿真得到了闭门器流道的压力云图和速度流线图。 为保证计算结果的准确性,同时缩短计算时间,笔者对于阻尼孔、节流阀采用较细化的网格,而对结果影响不大的部分采用密度稍大的网格[15]。 柱塞位于阻尼孔1和节流阀1之间时,闭门器的内部压力如图8所示。 图8 柱塞位于阻尼孔1和节流阀1之间的压力云图 此时油液从节流阀2和两阻尼孔流出左腔,从节流阀1流入右腔,此时柱塞两边的压力差为0.04 MPa。 柱塞位于阻尼孔1处时,闭门器的内部压力如图9所示。 图9 柱塞位于阻尼孔1处的压力云图 此时油液从节流阀2和阻尼孔1流出左腔,从节流阀1流入右腔,此时柱塞两边的压力差为0.029 MPa。 柱塞运动至两阻尼孔处时,闭门器内部压力如图10所示。 图10 柱塞运动至两阻尼孔处的压力云图 此时油液从节流阀2流出左腔,从节流阀1流入右腔,此时柱塞两边的压力差为0.017 MPa。 闭门器实际安装如图11所示。 图11 闭门器安装示意图 通过计算可知,当门的开度为120°~150°时,柱塞位于阻尼孔1和节流阀1之间;当门的开度为70°~90°时,柱塞位于阻尼孔1处;当门的开度为16°~53°时,柱塞运动至两阻尼孔处。 笔者把门扇打开到最大开度后,使其自动关闭,测量关门过程中门扇经过几个固定角度所需要的时间,通过计算将门转动的角度换算为柱塞齿条移动的距离,由此计算出柱塞齿条在不同位置的移动速度,如表2所示。 表2 试验的关门速度 笔者将柱塞处于不同位置时的运动速度代入柱塞齿轴处于不同位置段时的速度与阻尼力关系曲线中,可以得到:当柱塞位于阻尼孔1和节流阀1之间时,柱塞两边压差约为0.048 MPa;当柱塞位于阻尼孔1处时,柱塞两边压差为0.03 MPa;当柱塞运动至两阻尼孔处时,柱塞两边压差为0.015 MPa。 考虑到模型简化造成的误差,由此可见,计算结果和流场仿真结果相近,能反映闭门器实际工作状况。 笔者测量每隔5°时的开门力和关门力,测量结果如表3所示。 表3 试验的开关门力 笔者选取柱塞位于阻尼孔1和节流阀1之间、位于阻尼孔1处和位于两阻尼孔中间这3处位置,对比实际关门力和理论关门力,结果如表4所示。 表4 试验关门力和理论关门力 由表4可知,试验结果、数学计算和流场仿真结果基本吻合,由于在闭门器复位过程建模时对结构的适当简化,忽略了柱塞齿条和筒壁之间的缝隙、油液压缩等因素的影响,仿真得到的关门力和试验测得的关门力相比有一定的误差。 针对某型号液压闭门器的寿命测试合格率低的问题,笔者对该闭门器工作时柱塞所受阻尼力进行了理论计算、仿真分析和试验测试研究;首先应用流体力学理论,推导出了液压元件阻尼力的计算公式,建立了和柱塞行程相关的闭门器阻尼力数学模型;运用ANSYSFluent分析闭门器流道模型,得到了流道内部压力变化及主要受力点,通过试验台试验数据和软件仿真结果的对比,对数学模型进行了验证。 研究结果表明: (1)数学计算和Fluent仿真所得柱塞两端压力差误差为0.001 MPa~0.008 MPa; (2)理论关门力和实际关门力误差为2.6 N~3.5 N; (3)试验结果、数学计算和流场仿真结果基本吻合,证明所建数学模型的准确可靠。 在之后的研究中,笔者将在不影响闭门器使用性能的基础上,对阻尼孔和节流缝隙进行结构优化,以提高闭门器的可靠性。2 不同位置段时速度与阻尼力关系

2.1 柱塞位于阻尼孔1和节流阀1之间时的压力
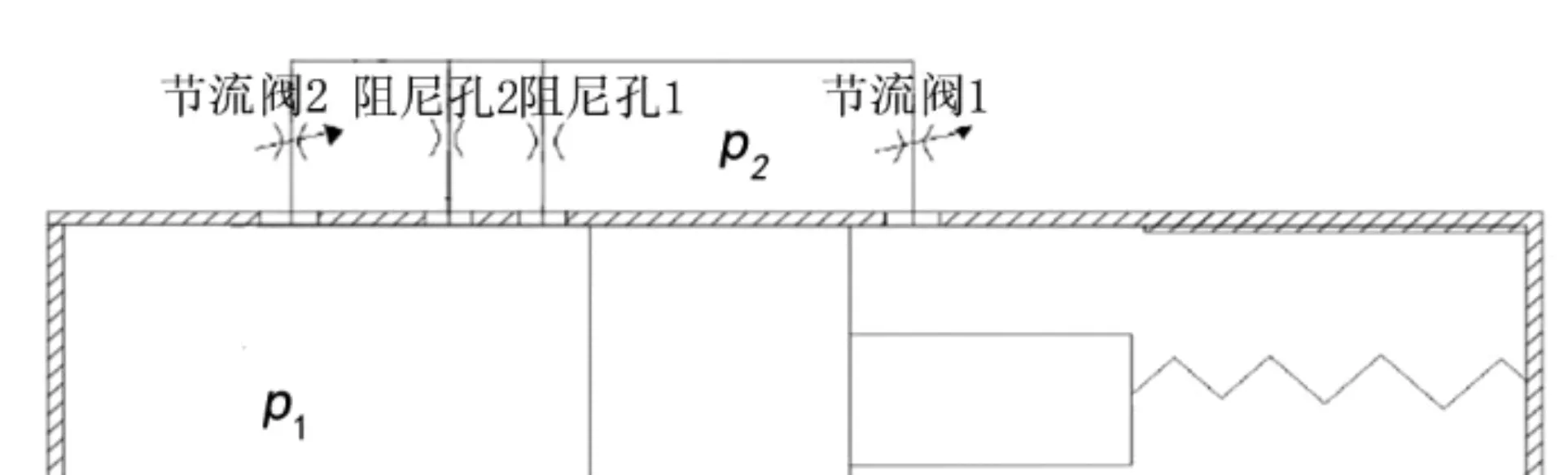
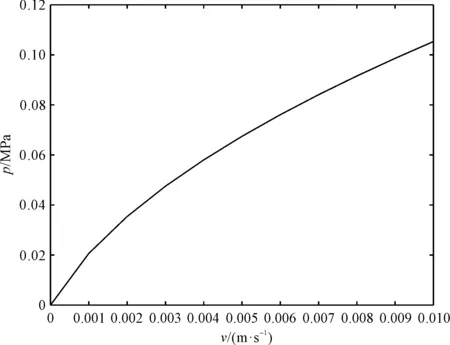
2.2 柱塞位于阻尼孔1处的压力
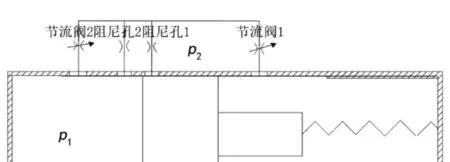
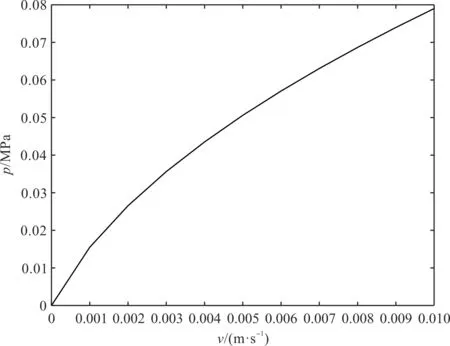
2.3 柱塞运动至两阻尼孔处的压力
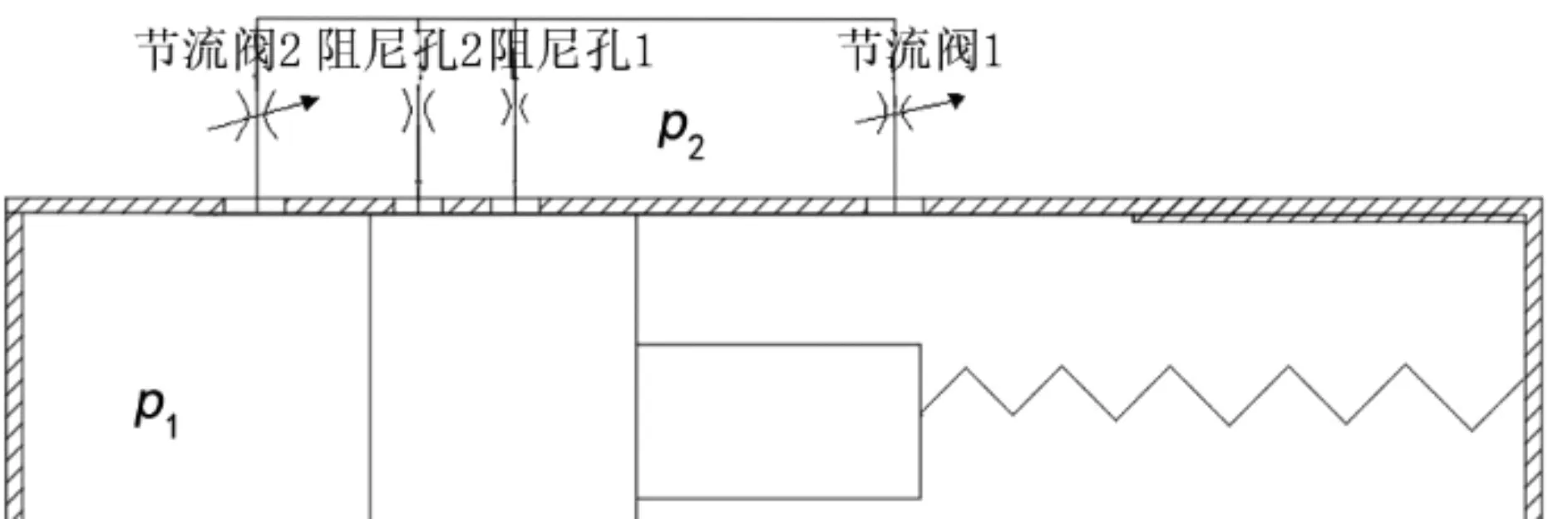
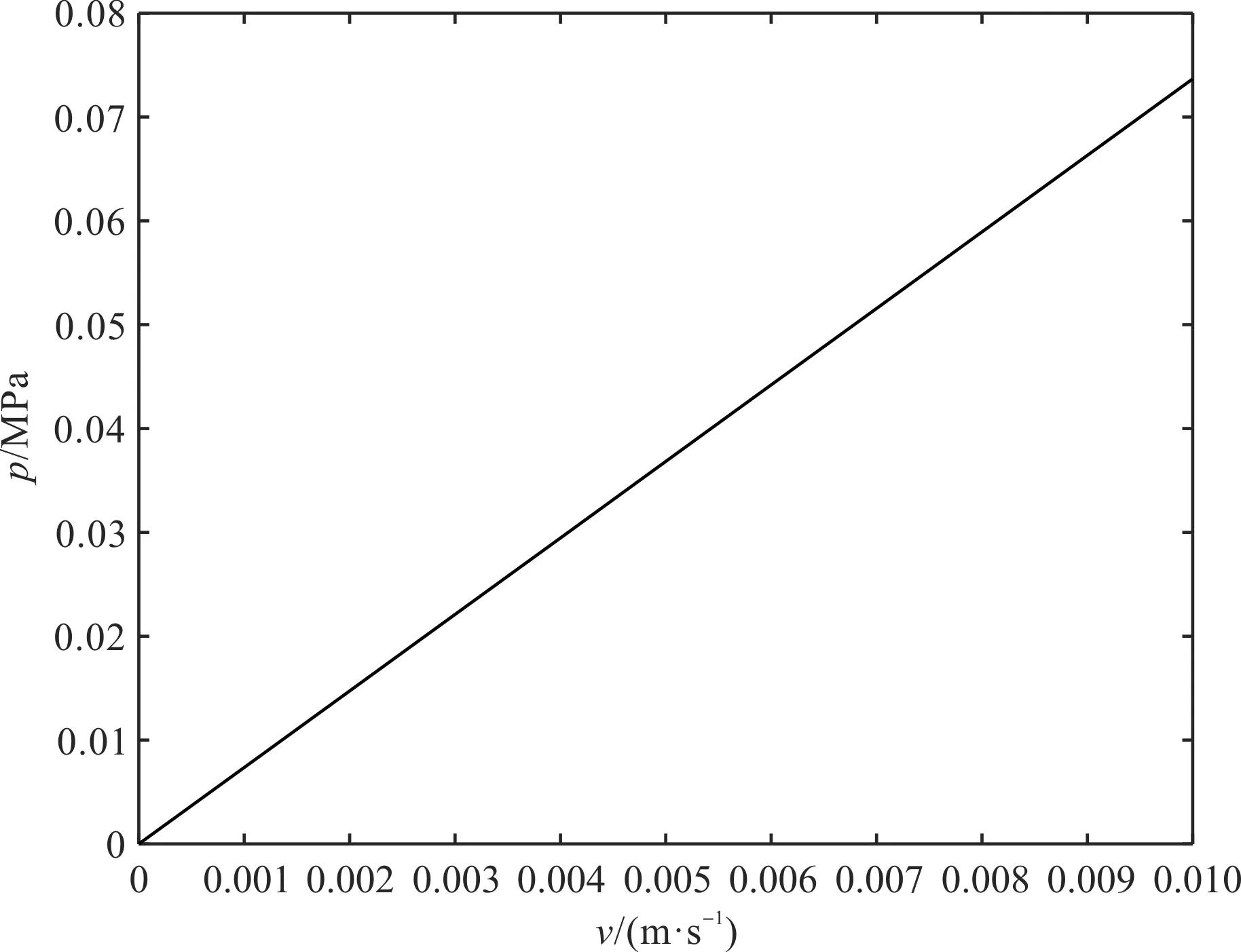
3 阻尼元件流场仿真
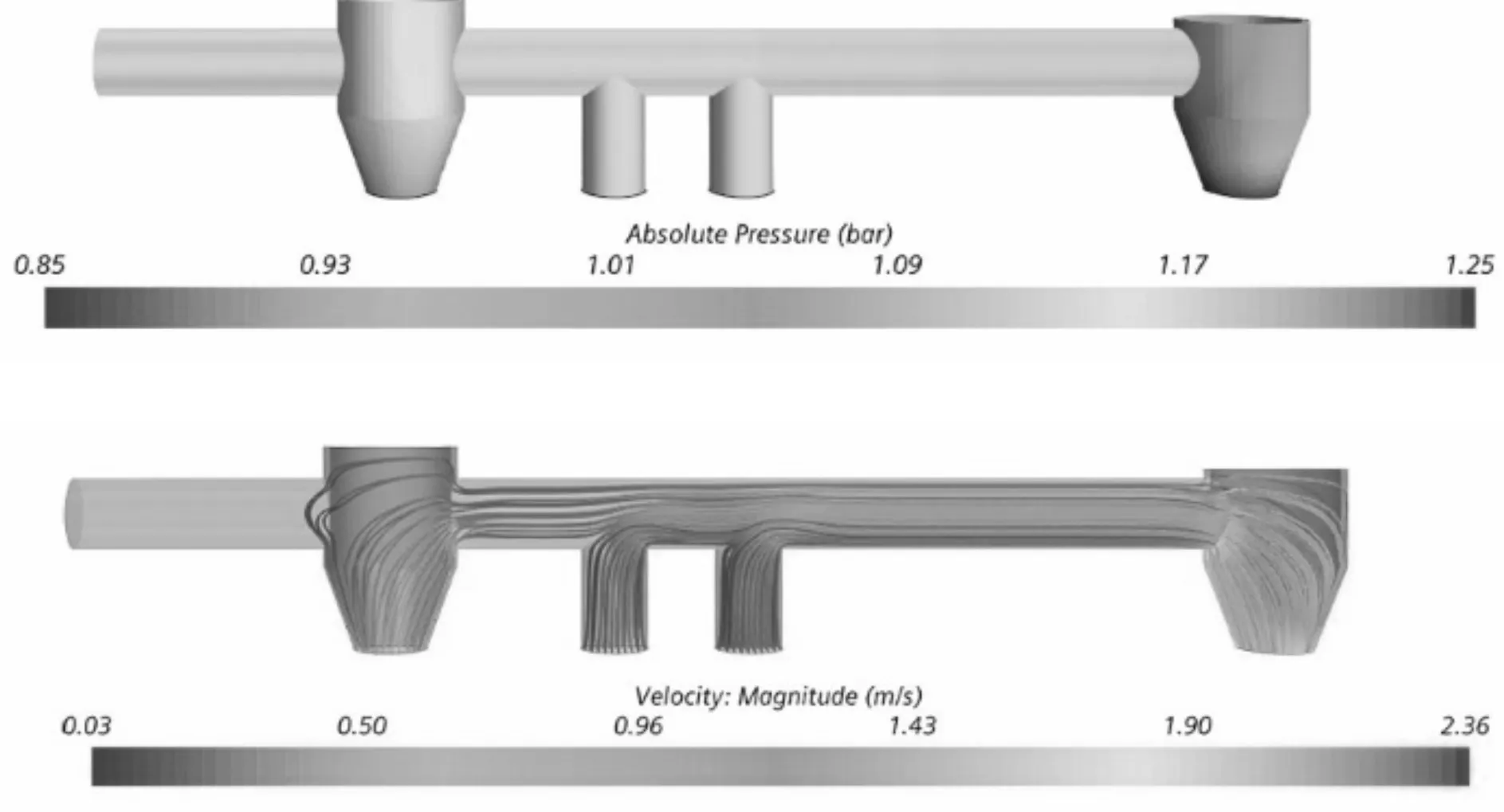
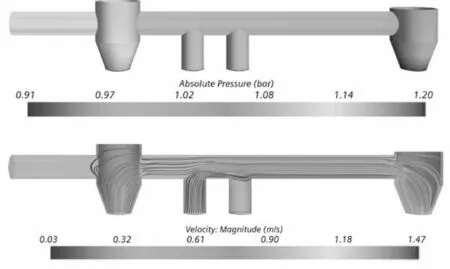

4 试验及结果分析

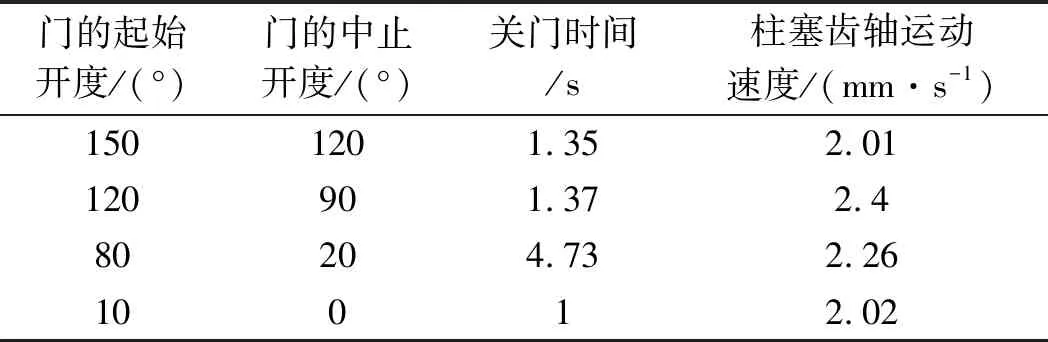
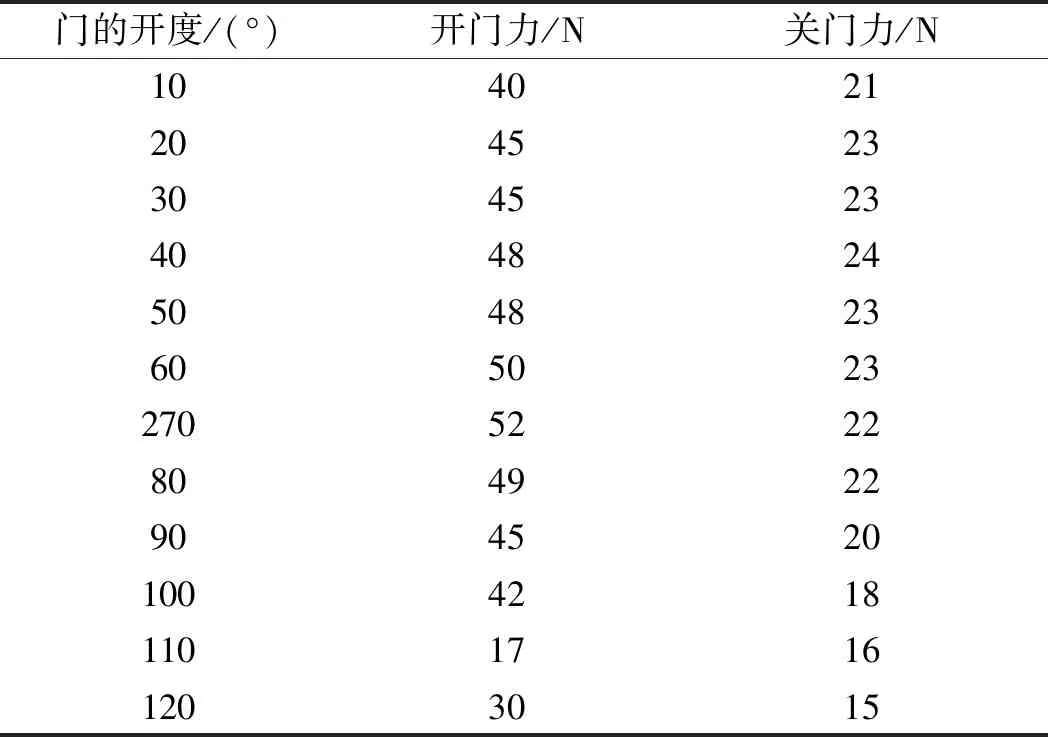

5 结束语

