基于卷积孪生神经网络的滚动轴承故障定位方法*

刘 岱,常东润,孙习习,陈 斌

(1.中国民航大学 安全科学与工程学院,天津 300300;2.中国民航大学 电子信息与自动化学院,天津 300300)

0 引 言

作为大型机械设备的旋转部件,滚动轴承被广泛应用在风力发电、航空航天、铁路运输等领域。当轴承发生故障时,可能会引起机械设备失效,造成经济损失,引发安全事故。因此,对轴承的故障进行诊断和状态监测极为重要。

传统的故障诊断包括3个步骤[1]:信号采集处理、特征信息提取和故障类型辨识。近年来,深度学习算法凭借优秀的特征提取和模式辨识能力,在滚动轴承故障诊断领域得到了快速发展。其中,最为常见的深度学习模型[2]包括卷积神经网络(convolution neural network, CNN)、自编码器(auto-encoder, AE)和循环神经网络(recurrent neural network, RNN)等。

近年来,CNN被引入到故障诊断领域,且可以很好地提取出顺序数据中的有效特征。LECUN Y等人[3]在CNN[4]的基础上,构建了基于深度学习的LeNet-5模型。LI Chun-lin等人[5]建立了基于时间编码序列和CNN的故障诊断方法。

自编码器是由RUMELHART D E[6]提出的一种尝试将输入复制到输出的无监督网络模型。通过改进编码和解码两部分的网络结构,自编码器又被发展为:稀疏自编码器(sparse auto-encoder, SAE)、堆叠自编码器(stacked auto-encoder, SDAE)和降噪自编码器(denoising auto-encoder, DAE)等网络。

曹浩等人[7]采用堆栈系数自编码器,对基于奇异值分解和时域分析方法提取的故障特征进行了优化,通过SoftMax分类器实现了对非平稳振动信号的特征分类。MAO Wen-tao等人[8]融合了极限学习机高训练效率和堆叠自编码器高分类准确率的优点,提出了一种基于极限学习机和堆叠自编码器的轴承故障诊断模型。

1990年Pollack[8]首次提出了循环神经网络(RNN)。RNN主要利用时间序列之间的关联性来提取样本的特征信息。LIU Han等人[9]提出了一种基于RNN的自动编码器(auto-encoder,AE)诊断滚动轴承故障。但是,RNN始终存在一个缺陷,即在网络训练的反向传播过程中,RNN容易发生梯度消失或梯度爆炸[10]。

为了改善RNN的梯度消失问题,研究人员提出了长短期记忆网络(long short-term memory networks, LSTM)和门控循环单元网络(gated recurrent unit networks, GRU)[11]。刘春晓等人[12]基于CNN和RNN的优点,搭建了一种时空神经网络,采用深度残差网络的并联思想,将卷积层和LSTM层并联起来,以此作为模型的复合卷积层;同时,选取振动信号的时域和空间域特性作为输入特征,以提升模型的特征表达能力。

在使用时,上述基于传统深度神经网络的故障定位方法需要满足数据同分布的要求,一旦负载、转速或工作设备发生变化,原有的网络模型就要重新调整结构和参数。因此,反复地训练轴承的数据集,必然无法满足工业故障诊断便捷性、快速性及准确性的需求。

因此,笔者针对同一设备不同工况及不同设备不同工况下数据分布不一致的情况,选用擅长处理样本相似性度量的孪生网络[13](Siamese neural network, SNN)作为诊断框架,提出一种基于随机池化-ELU-孪生卷积神经网络(stochastic pooling ELU-Siamese convolutional neural network, SE-SCNN)的有监督学习模型。

1 基于孪生网络的特征模型

孪生网络是一种基于权值共享的深度学习算法,在1993年提出后被广泛用于解决样本相似性度量的问题。基于孪生网络的特征度量模型将一对样本输入至两个结构相同、权值共享的子网络中,通过同一个特征映射函数得到两个特征向量,利用欧式距离计算特征向量之间的相关性,从而输出样本之间的相似程度。

此处采用孪生网络作为轴承故障定位的基本框架,即将美国辛辛那提大学智能维护系统中心(IMS center)提供的航空轴承运行数据,经过预处理,与未知工况的其他设备数据组成样本对作为网络输入,将提取到的故障信息对映射到低维特征空间中,通过比较特征信息之间的距离确定故障类型,然后借助分类器实现轴承故障定位。

为了避免特征相近的样本被映射到特征空间的不同位置,孪生网络的子网之间采用共享权值和损失函数来减少模型误差。

基于孪生网络的特征度量框架如图1所示。

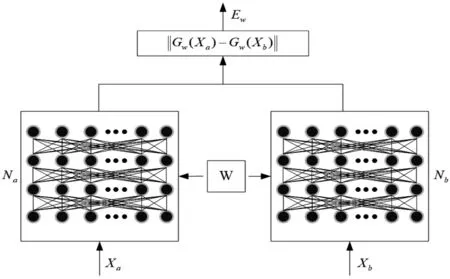
图1 孪生网络结构图

Xa和Xb分别为一对输入样本,Na和Nb为两个完全相同的子网络,共享权重W;输入样本对通过两个子网络映射到同一特征空间,分别得到特征向量Gw(Xa)和Gw(Xb);通过计算每一个特征向量对之间的欧氏距离判断输入样本之间的相似度。

具体公式如下:

Ew=‖Gw(Xa)-Gw(Xa)‖

(1)

式中:Ew—特征向量对之间的欧氏距离。

Ew值越小,表示在特征空间中的距离越近,样本类型相同的概率越大。同时,对于n个训练样本来说,基于孪生网络的深度学习框架可以构建n(n-1)个样本组合,能够有效扩充样本的数据量,提高模型的训练次数,具有很强的鲁棒性。

2 基于SE-SCNN的轴承故障定位模型

2.1 SE-CNN模型

滚动轴承的振动信号是非平稳非线性的一维时间序列信号,而传统的CNN具有平移性、缩放不变性,在信号处理方面具有不可比拟的优越性。

笔者选取一维CNN作为孪生网络的子网结构。由于多工况轴承数据集具有海量性、复杂性等特点,传统CNN存在因输入数据分布不一致导致网络收敛性能不佳的问题;笔者在池化策略和激活函数方面对一维CNN进行改进,得到改进卷积神经网络:随机池化-ELU-CNN(stochastic pooling ELU-CNN, SE-CNN)。

在池化策略上,最大池化和平均池化是CNN中最常用的两种池化方法:(1)最大池化在对特征信息进行运算时,仅考虑池化区域中最大的元素,忽略了潜在的特征信息;(2)平均池化虽然统筹考虑了所有元素的信息,但过度削弱了核心元素在全局中的作用,特征表达能力有限。

除此之外,对于小样本的训练数据而言,这两种池化方法更容易增加网络过度拟合的风险。因此,为克服最大池化和平均池化的不足,笔者综合考虑特征元素的全局信息和局部信息,选择基于正则化算法的Stochastic池化策略,融合池化区域内每个元素的概率值进行随机采样。

(1)首先,对区域内的所有元素进行标准化处理,计算概率矩阵,具体公式如下:

(2)

式中:pi—激活元素ai的采样概率;Rj—池化核的位置。

(2)然后,基于概率分布进行采样,获得新的特征元素值:

(3)

ReLU是目前深度神经网络中最常用的非负激活函数,有效解决了传统激活函数Sigmoid、Tanh等的梯度消失问题,但ReLU函数自身带来的均值偏移和神经元死亡现象,严重影响了深度神经网络的收敛性能。

针对以上问题,笔者选择ReLU的改进变种函数ELU作为激活函数。ELU具有软饱和性,能够减轻噪声对网络的影响,其具体定义为:

(4)

式中:α—大于0的超参数,负责控制输入小于零的部分饱和值的大小。

2.2 轴承故障定位模型

针对原始孪生网络子网结构简单,导致特征提取性能不佳的问题,笔者在孪生网络的基础上,引入SE-CNN作为子网部分,构成一维随机池化-ELU-孪生卷积神经网络(SE-SCNN)轴承故障定位模型。

变工况下轴承数据集分布不同,会导致模型训练效率不高,因此,笔者将SE-SCNN模型分为两个阶段,即预训练阶段和模型训练阶段;根据具体性能的不同,每一阶段的模型又分为特征提取器和分类器两部分。

其中,特征提取器为SE-CNN结构,主要利用改进后的CNN提升模型的特征提取性能;分类器部分则采用SoftMax分类,用于对轴承特征距离进行进一步的分类,以实现对轴承故障进行定位。

预训练网络作为SE-SCNN模型的子网部分,采用单输入的SE-CNN网络,具体结构如图2所示。

图2中,网络主要对模型的特征提取器进行初始的参数优化,以便于后续SE-SCNN网络的训练。

在预训练阶段,已标记的轴承样本经特征提取器映射到特征空间,然后由分类器利用损失函数将特征信息映射到类别空间,利用最小化预训练网络的损失函数得到SE-SCNN模型的初始化参数,提高了模型的故障定位性能。

SE-SCNN故障定位模型的整体结构如图3所示。

图3中,子网部分采用与预训练网络相同的结构,均由特征提取器和分类器组成。针对单一损失函数难以同时满足模型的特征度量性能和故障定位性能的问题,SE-SCNN模型的关键在于采用基于对比损失和分类损失的联合损失函数作为目标函数,各子网之间保持权值共享,分别从变工况轴承数据集中接收一对不同的样本作为模型输入,通过特征提取器将样本对中的故障信息映射到特征空间,利用对比损失函数计算故障特征对之间的相似度。同时,每一个子网又连接至一个独立的分类器得到输出类别,通过分类损失函数衡量模型的分类效果。

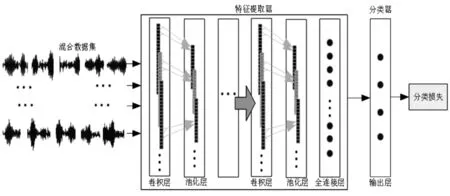
图2 基于SE-SCNN故障定位模型的预训练网络

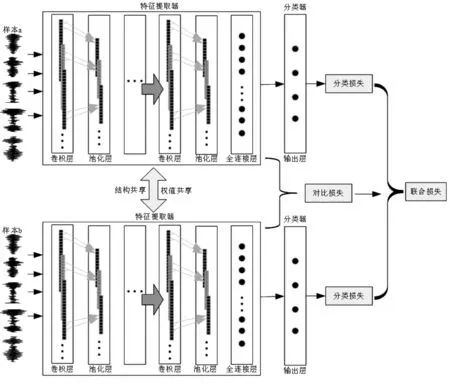
图3 基于SE-SCNN的故障定位模型

在SE-SCNN故障定位模型的子网结构中,特征提取由输入层、4个连续的卷积层和池化层、2个全连接层和1个Batch Normalization层组成,而后把特征向量经分类器SoftMax层输出。

具体SE-SCNN网络结构参数如表1所示。

表1 SE-SCNN网络结构参数设置

网络结构中,卷积层和池化层的填充方式均为padding=“same”,以保证输入输出之间特征大小不变。

2.3 基于SE-SCNN的轴承故障定位流程

基于SE-SCNN的轴承故障定位方法的整体流程如图4所示。

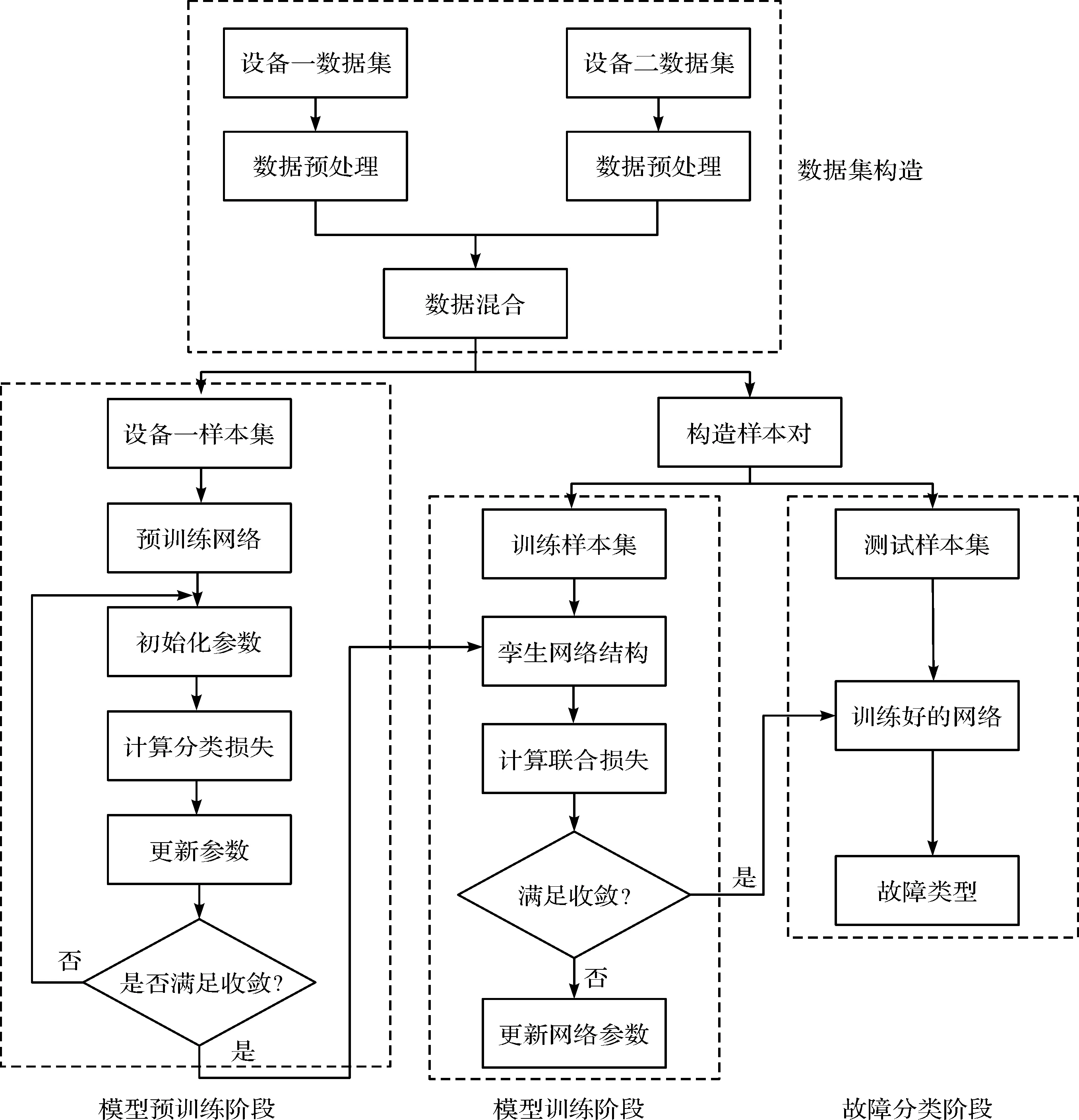
图4 基于SE-SCNN的轴承故障定位流程图

图4中,定位流程总共分为4个阶段,即数据集构造、模型预训练、模型训练和故障分类。

(1)数据集构造。将IMS数据集作为设备一数据,根据故障起始时间选取健康数据和故障数据,组成预训练样本集;将德国Paderborn大学的变工况轴承数据集作为设备二数据,对其分别进行降采样、滑窗、归一化等数据预处理操作,得到2个数据集各自的训练集和测试集,对应拼接,并随机打乱,最终获得混合工况下的SE-SCNN孪生模型基准样本集;

(2)模型预训练。构建基于特征提取器和SoftMax层分类器的预训练模型;初始化网络参数将由设备一得到的训练样本集输入模型中进行训练,通过最小化分类损失函数优化模型的性能,优化结束后保存其网络参数,以提升模型训练的效率;

(3)模型训练。利用(2)中预训练后的模型作为孪生网络的子网部分,搭建SE-SCNN网络模型,从混合基准样本集中随机抽取构造成对的输入样本,通过前向传播计算网络的联合损失函数,使用反向传播算法反复迭代更新模型参数,充分提升模型的特征提取性能和分类性能;

(4)故障分类。利用混合样本集的测试集样本,成对输入到已经训练好的网络模型中,经分类器获得故障定位结果。

3 实验与结果分析

3.1 数据集描述

3.1.1 设备一数据集描述

笔者采用美国辛辛那提大学智能维护系统中心(IMS Center)提供的轴承数据集1中的轴承3、轴承4振动数据和数据集2中的轴承1振动数据。

实验轴承转速均为2 000 r/min,仅3号轴承受径向载荷为26.6 kN[14]。为了平衡故障数据集和健康数据集的比例关系,这里以轴承各自的故障起始点为坐标点,分别对3个轴承数据向左随机选取70个正常数据样本[15],构成设备一的健康数据集;向右取固定数目的故障数据构成内圈故障样本、外圈故障样本和滚动体故障样本。

设备一原始数据集信息如表2所示。

表2 设备一原始数据集信息

3.1.2 设备二数据集描述

设备二数据集来自德国Paderborn大学提供的旋转轴承数据集[16]。实验平台如图5所示。

图5 帕德伯恩轴承实验平台

该平台包含多个模块,其中,轴承测试台用于产生不同损伤类型的实验数据,径向力为1 000 N,电机转速和负载转矩均为工况变量,数据采样频率为64 kHz。

此处所用轴承型号参数如表3所示。

表3 设备二轴承型号参数

该数据集包含人工故障数据和轴承真实损伤数据,有3种状态类型:健康、内圈故障和外圈故障。

为了验证该方法具有较强的泛化性,笔者保持负载转矩为0.7 N·m不变,在仅仅改变电机转速的情况下,得到了设备二的原始变工况数据集,如表4所示。

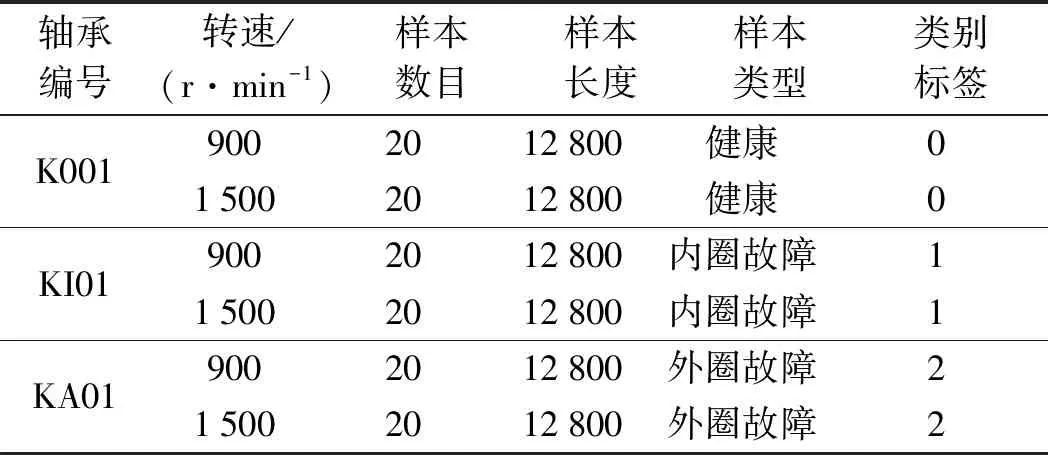
表4 设备二原始数据集信息

笔者选取设备二较少的数据样本,以满足实际多工况下的小样本数据集特点。

3.2 混合数据集构造

由于预训练网络和SE-SCNN的子网均采用相同的结构,为了便于模型的统一输入,同时减少计算资源,笔者分别对设备一和设备二的数据集进行相同的数据预处理操作。

考虑到实际工业采集系统,为方便存储大量历史数据,此处普遍采用间隔采样的方式。

为了模拟实际信号的采样数据量,笔者首先将原始信号采样频率降至工业常用的5 000 Hz,缩短数据长度至5 000;然后对数据进行无重叠的滑窗处理,设置截断长度为1 000(在进一步缩短数据长度的同时,有利于扩充样本集,避免训练过程中的过拟合现象);最后,为了加快卷积网络的训练,将输入数据处理成具有相同量级的规范数据,对所有样本进行归一化处理。

在上述实验中,笔者预训练网络的数据集来自设备一预处理后的数据,按照7 ∶3随机抽取组成预训练模型的训练集。

为了模拟实际工程中变工况、跨设备的复杂采集环境,笔者打乱两个数据集分别按照同样比例划分训练集和测试集,对应拼接训练集的数据和标签以及测试集的数据和标签,再从中随机抽取一定比例的训练集和测试集作为SE-SCNN孪生模型的混合样本集。

其中,混合样本信息如表5所示。

表5 混合样本集信息

3.3 结果与分析

为了验证笔者提出的SE-SCNN模型的有效性,针对网络有无孪生结构,以及是否改进池化策略和激活函数,笔者构建CNN、SE-CNN、SCNN、SE-SCNN等4种模型,从特征提取性能、故障定位准确程度、收敛速度3个方面,比较模型对混合数据集的故障定位性能。

基于单输入的预训练网络,CNN、SE-CNN模型参数设置与SCNN、SE-SCNN相同,即均采用“特征提取器+分类器”的结构;其中,CNN、SCNN池化策略设置为常用的最大值池化,激活函数为ReLU。

4种模型的训练过程参数设置如下:epochs=150,batch_size=64,初始学习率lr=0.001。

3.3.1 故障定位性能综合评价指标

由于单一的指标不能很好地评估模型的性能,因此,笔者将常用的准确率Acc,精确率Pre,召回率Re和F1值(F1-score)作为模型故障定位准确程度的评价指标。

其中,每个指标的计算公式如下:

(5)

(6)

(7)

(8)

式中:TP—正确分类的正样本数;TN—正确分类的负样本数;FP—正样本的误分类样本数;FN—负样本的误分类样本数。

3.3.2 故障定位性能对比与分析

考虑到单次实验结果往往误差较大,为了说明各模型的故障定位性能,笔者从混合数据集中随机抽取10次测试集进行实验,取不同指标的平均值作为最终实验结果,如表6所示。

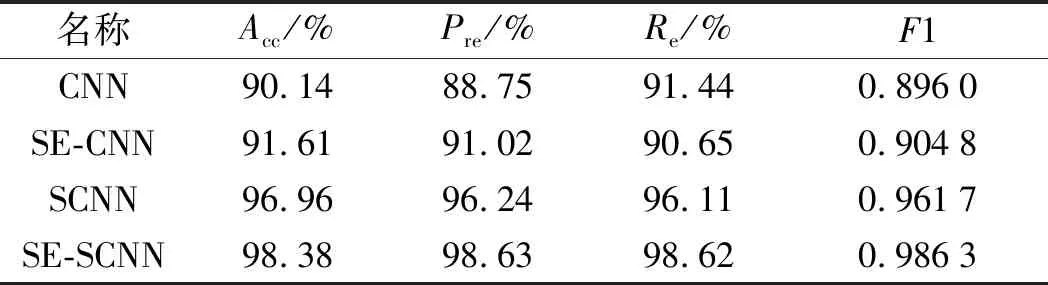
表6 不同模型的定位准确程度

从表6中可知:相对于CNN来说,在各类性能指标上,基于孪生结构的SCNN和SE-SCNN模型都具有很大的优越性,其准确率均达到了95%以上;

其综合数据指标F1也充分表明,在不同的工况下,笔者所提的SE-SCNN模型都有着较好的分类效果;特别是在跨设备的情况下,与同结构的SCNN相比,该模型故障定位准确程度有明显提高。

3.3.3 模型收敛性能对比与分析

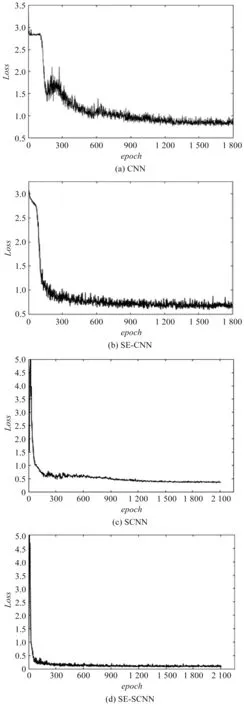
图6 不同模型的Loss收敛曲线图

笔者通过训练过程的损失函数-迭代次数曲线,证明SE-SCNN模型的快速收敛性,如图6所示。图6分别展示了4组模型的损失函数下降曲线。首先,从收敛速度来看,在同一迭代次数下,采用Stochastic池化策略和ELU激活函数的SE-CNN、SE-SCNN下降速度明显高于另外两种模型,且收敛曲线更加平滑,具有较强的稳定性;

其次,比较SE-CNN和SE-SCNN可以发现,后者的损失函数到达平稳状态时,损失函数值更小,具有更好的分类性能。

4 结束语

由于不同设备及不同工况下,滚动轴承振动数据分布存在差异,传统深度学习模型难以适应数据集分布的不一致,为此,笔者提出了一种基于卷积孪生神经网络SE-SCNN的轴承故障定位方法,即利用基于样本相似性度量的孪生结构,通过特征提取器,将一对不同设备、不同工况的样本数据映射到特征空间中,进行距离计算;结合分类器得到特征向量在类别空间的映射结果,实现混合数据集下的故障定位。

笔者通过集合两种数据集的混合数据集进行了实验,结果表明:

(1)与其他方法相比,基于SE-SCNN的故障定位方法的3项性能指标准确率均为最高,且都在95%以上,综合评价指标比其他先进方法提高了0.024 6,在模型的定位准确度方面具有明显优势;

(2)在收敛性方面,采用Stochastic池化策略和ELU激活函数的SE-SCNN模型,收敛曲线更平滑的同时,损失函数值也更小,在稳定性和分类性能具有明显优势。

除了轴承采集装置本身的多工况设定外,传感器采集的振动信号会混入背景噪声,淹没故障特征信息,导致轴承故障诊断开展困难。因此,在未来的研究工作中,笔者可尝试对信号进行有效去噪处理,以提高工业场景下轴承设备的智能故障诊断性能。