基于两相流空穴模型的比例阀流量特性分析*

谭正生

(重庆化工职业学院 智能制造与汽车学院,重庆 401228)

0 引 言

在大型柴油机的供油系统中,高压油泵比例阀控制液压油的流量,而不同工况下的进油量需求不同。在低工况小流量控油时,需求控油精准,而在高工况大流量控油时,需求控油响应快[1]。

通常情况下,通过改变节流阀口大小和形状可以获得不同阀芯位移流量特性曲线,因此,深入研究比例阀的节流窗口形状对液压工程机械流量特性和结构优化具有重要意义[2,3]。

以液压控制系统比例阀作为研究对象,不少国内外学者采用计算流体动力学方法,分析了阀的性能。

冀宏等人[4]在对滑阀进行研究时,基于压差特性试验和阀口面积计算,分析了滑阀矩形节流槽阀口的流量系数。傅新等人[5]在对非全周开口滑阀液动力进行研究时,采用CFD方法,分析了U、V形节流槽滑阀流量特性以及其详细的流场情况。SHIGERU O等人[6]在进行水压提升阀中的气蚀效应研究中,进行了空化对液压阀的影响研究。

在对阀的性能进行研究时,大多数研究人员未考虑其节流阀口的空穴。而实际上,在阀的节流位置,其一旦达到空穴压力,介质极易产生空穴现象,严重的空穴现象会影响阀的流量特性[7-11]。

因此,笔者基于CFD两相流空穴模型,结合比例阀流量特性实验的方法,分析3种不同阀口形状的比例阀流量特性以及空穴情况。

1 计算流体模型与实验

1.1 计算流体模型

笔者以某型比例阀作为研究对象,在电磁力、复位弹簧的作用下控制比例阀的电磁力,使阀芯保持在某一开度,以输出相应的控制流量[12]。

该比例阀的三维剖面结构如图1所示。

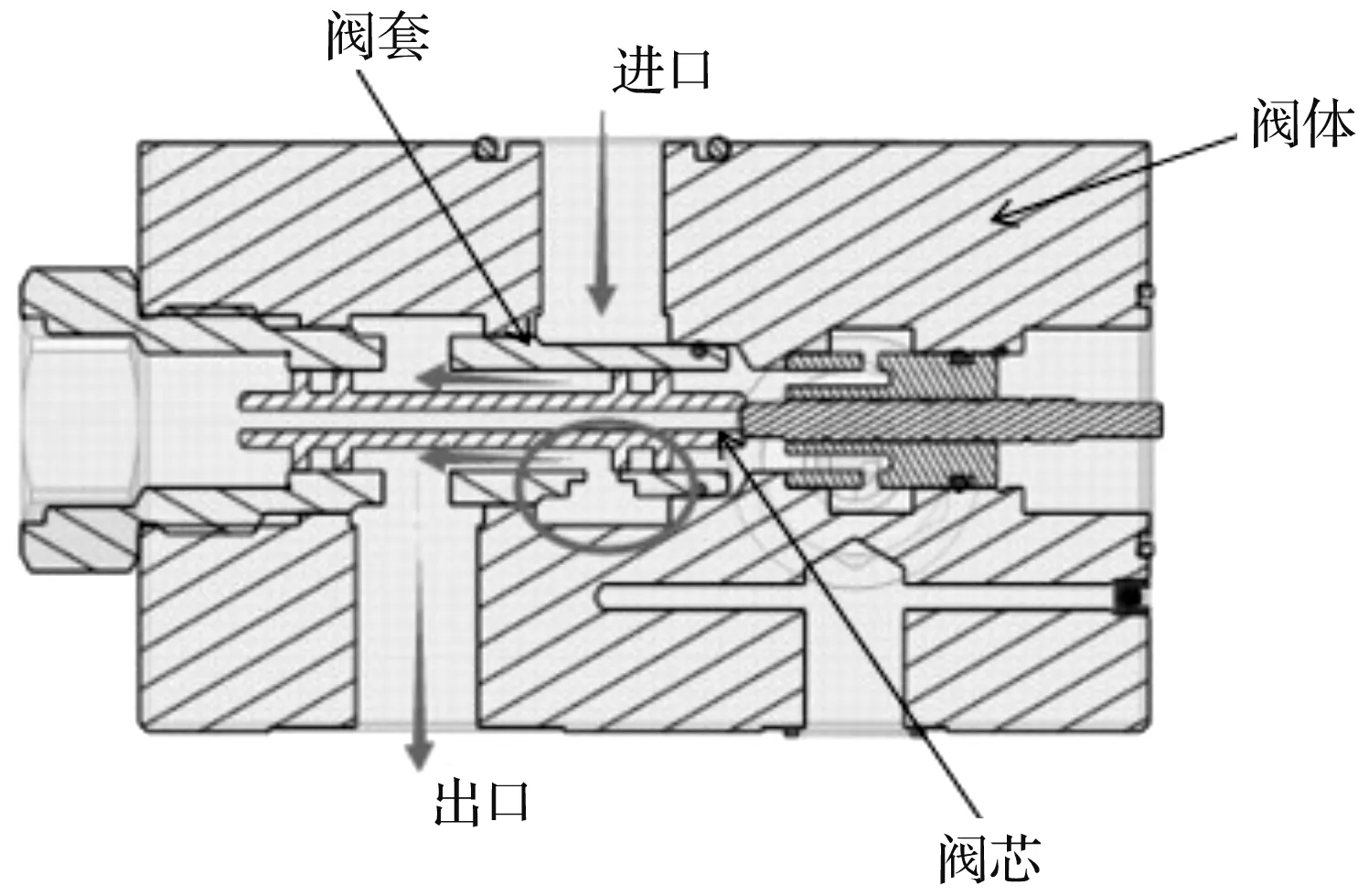
图1 比例阀剖面结构

图1中,比例阀主要包括阀体、阀套以及阀芯等结构(箭头指示方向为流体流动方向)。图中标记的圆圈为阀套节流窗口位置。

阀套节流窗口的3种结构如表1所示。

表1中,3种结构的最大开度的阀口面积均为8 mm2。其中,结构1阀口为矩形,矩形阀口宽为2 mm,长为4 mm;结构2阀口为二节矩形,第一阶矩形宽为1 mm,长为2 mm,第二阶矩形宽为3 mm，长为2 mm;结构3阀口为三角形,最大开度为4 mm。

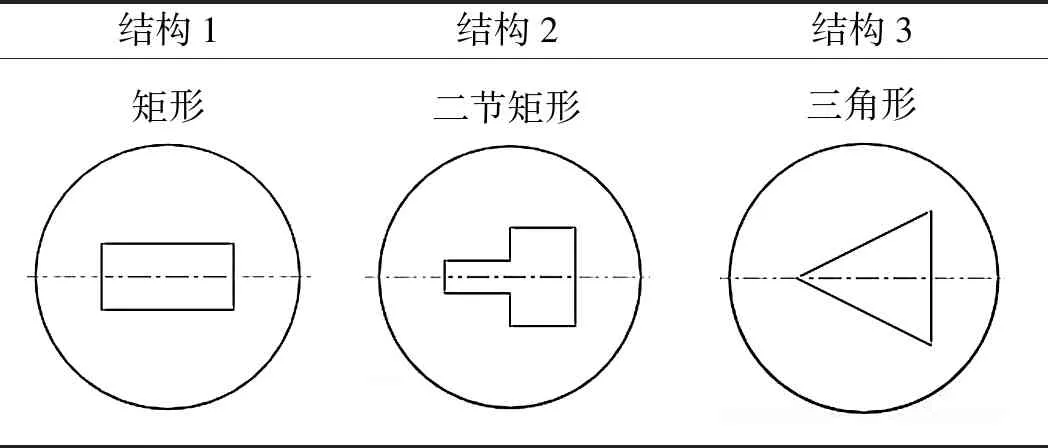
表1 阀口结构

因为计算流体域直接建模复杂,所以笔者在ANSYS/DM中抽取流道,其三维模型结果如图2所示。

图2 计算流体模型

1.2 比例阀性能实验

为了对照仿真结果,笔者在比例阀性能实验台上完成3种阀口的实验流量测试。测试过程要保证实验与仿真相同的压力边界条件,实验台通过调节直流电流的大小,控住比例阀的开度,通过进出油流量计获得比例阀的流量。

实验系统原理示意图如图3所示。

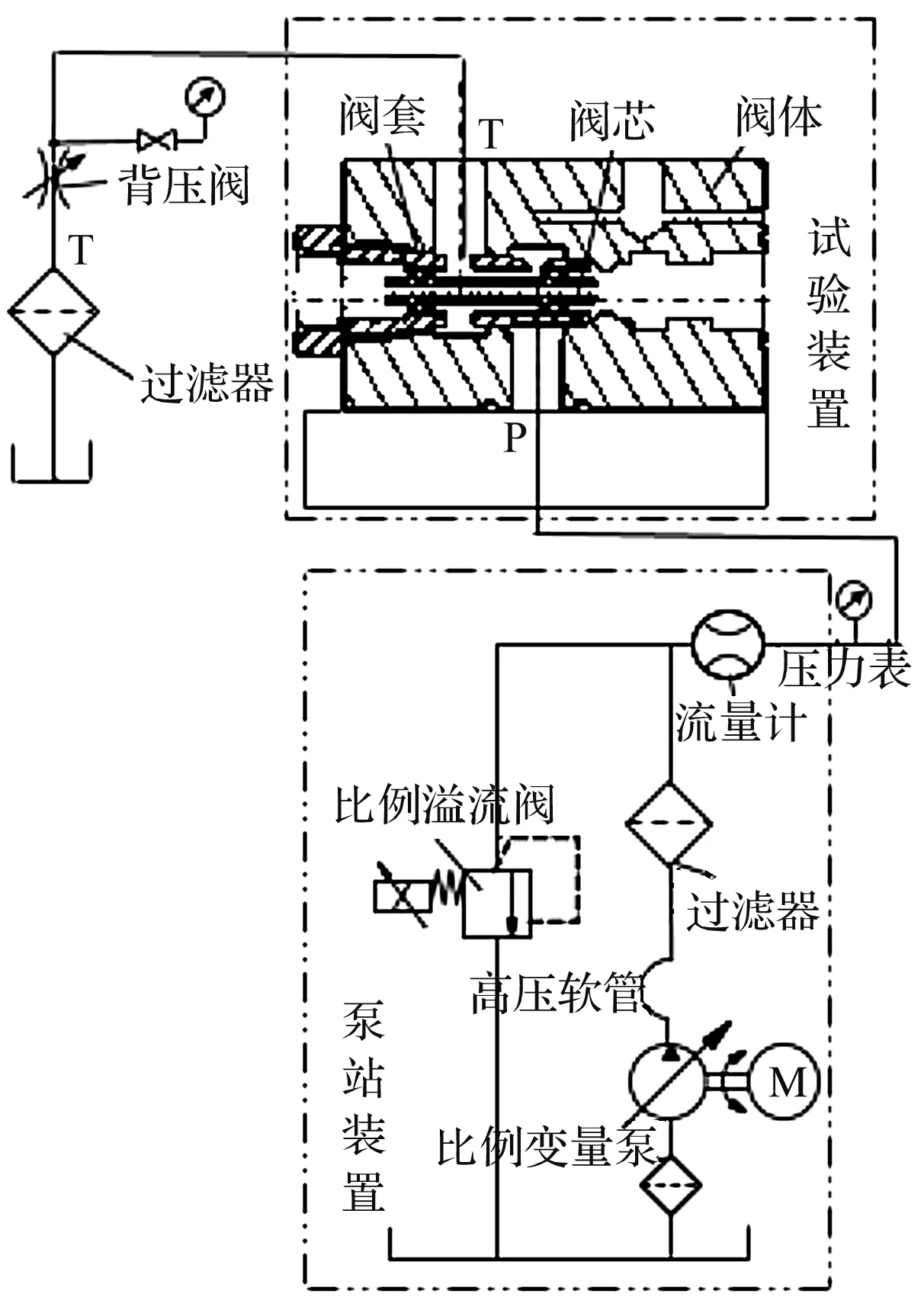
图3 比例阀性能实验系统原理图

2 空穴模型

比例阀计算域压力下降到设定流体饱和蒸气压以下,计算域中产生气体,并使气体溃灭,即产生空化现象。微型气泡周围压力降低时,气泡会逐渐地增大,从而形成空穴。

Fluent提供了Singhal空化模型、Zwart-Gerber-Belamri空化模型以及Schnerr-Sauer[13]空化模型。其中,Singhal空化模型对初生相和次生相有要求,不能与多相混合模型兼容,对欧拉多相流和LES湍流模型不可使用。

此处,进行比例阀空穴数值模拟计算时,液相和气相之间发生质量传递,因此,笔者选择Schnerr-Sauer空化模型[14-16]。

Schnerr-Sauer空化模型提供了气液两相传质方程。其中,空化模型中的体积分数的微分方程为:

(1)

式中:ρv—气相密度,kg/m3;ρl—液相密度,kg/m3;ρ—混合相密度,kg/m3;α—气相体积分数;Pv—液体饱和蒸气压,Pa。

净质量源相为:

(2)

气体体积分数和数量的关系式为:

(3)

将式(1,3)联立,可得:

(4)

式中:R—气液两相传质速率;Rb—气泡半径,m。

气泡半径Rb的表达式为:

(5)

式中:nb—单位体积气泡的数量,nb=1013/m3。

3 网格划分和边界设置

3.1 网格划分

因为计算域的形状不规则,节流口尺寸相对较小,所以流体计算域进行网格划分时,对模型采用四面体非结构网格划分,在计算域阀口节流位置进行网格加密。

节流口局部放大网格情况如图4所示。

图4 节流口网格

图4中,笔者在阀腔与节流口交接处进行了网格的局部加密。

网格划分完成后,笔者进行无关性验证。网格数量在8×105以上,流量在一定的范围上下波动,则认为网格数量对计算结果影响不大。最终,笔者确定计算模型的网格数量为8×105。

网格无关性验证如图5所示。

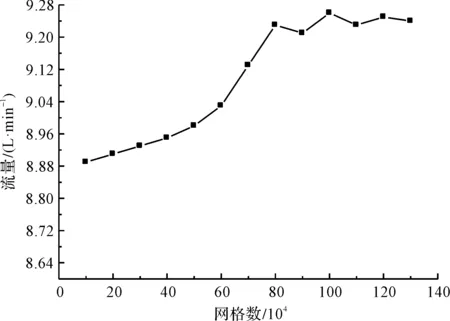
图5 网格无关性验证

3.2 边界和计算设置

笔者将网格模型导入ANSYS Fluent,进行多相流动仿真分析。

具体边界情况及Fluent计算设置如下:

(1)激活多相流模型的mixture子模块,采用mixture多相流模型[17]和Schnerr-Sauer空化模型计算比例阀流场;

(2)激活湍流模型。不考虑温度对计算的影响,所以不激活能量方程,油液接触壁面采用无滑移边界;

(3)分离求解器选择COUPLED,该求解器在Schnerr-Sauer空化模型中表现出更好的稳定性和收敛性[18-20];

(4)流体空间为油气两相流,液相为油,密度为870 kg/m3,运动黏度为0.016 7 kg/(m·s)。气体相设为空气,密度为1 kg/m3,黏度为7.0 e-06 kg/(m·s),空穴压力为320 Pa;

(5)边界设置:入口相对压力0.3 MPa,出口相对压力为0 MPa;

(6)Interface面设置:网格交界面中,如果存在流体流通的情况,则设置为Interface面;

(7)设置迭代计算精度,当进出口流量误差小于10-8时,计算结束。

4 仿真及结果分析

为了使研究结论具有一般性,笔者对比例阀变量因素采取无量纲化处理,即以阀口[21]某开度数值与阀口最大开度数值的比值作为研究过程无量纲变量,并以符号i(某开度数值x与最大开度数值w之比)作为当量开度。

阀口流量受流量系数、阀口面积、压差以及流体属性的影响,其流量关系式为:

(6)

式中:Ai—阀口面积,m2;i—阀口的当量开度,i=x/4(x—阀口开度,m);ρ—油液介质密度,kg/m3。

计算过程不考虑液体的可压缩性。

由此可得流量系数为:

(7)

式中:qv(i)—体积流量,L/min;Δp(i)—压差,Pa。

矩形阀口面积随当量开度的关系为:

Ai=8i(0≤i≤1)

(8)

二阶矩形阀口面积随当量开度的关系为:

(9)

三角形阀口面积随当量开度的关系为:

Ai=8i2(0≤i≤1)

(10)

笔者基于CFD两相流动Schnerr-Sauer空化模型的三维进行仿真计算,计算收敛后,先分析流场和空穴体积情况,再分析空穴下的流量特性。

4.1 流场及空穴分析

计算过程监测进出口流量,当绝对误差小于10-8时计算收敛。

在空穴模型下,数值模拟流场压力分布情况,结果显示,比例阀计算域压力变化主要集中在节流阀口区域,比例阀进口区域为高压区域,阀芯腔体为低压区域,进口区域和阀芯腔体的压力变化不大。

因此,此处的云图只分析节流位置变化情况。在不同当量开度下,3种结构阀口形状的节流口压力分布图,如表2所示。

表2 压力云图

从表2中的压力云图可知:在同一当量开度下,3种结构节流口处压力变化趋势相同,当量开度较小,节流口压力骤降,阀腔压力较小;当量开度较大,节流口压力下降较慢,阀腔压力升高,3种节流口的压力变化趋势相同。

由此可见,空穴模型下的3种结构阀口流场压力分布影响不大。

仿真过程中,笔者使用mixture多相流模型和Schnerr-Sauer空化模型计算比例阀流场,阀内局部油压低于饱和蒸汽压,流体从液态变成气态。

笔者计算的3种结构计算模型均有空穴产生,空穴的位置都在阀口处,而流体域其他位置未发生空穴现象,这主要是因为压降发生在节流口位置,导致该位置容易发生空穴现象。

但是3种结构的气相体积不同,因此,笔者统计了不同当量开度下,3种阀口结构的体积结果,如表3所示。

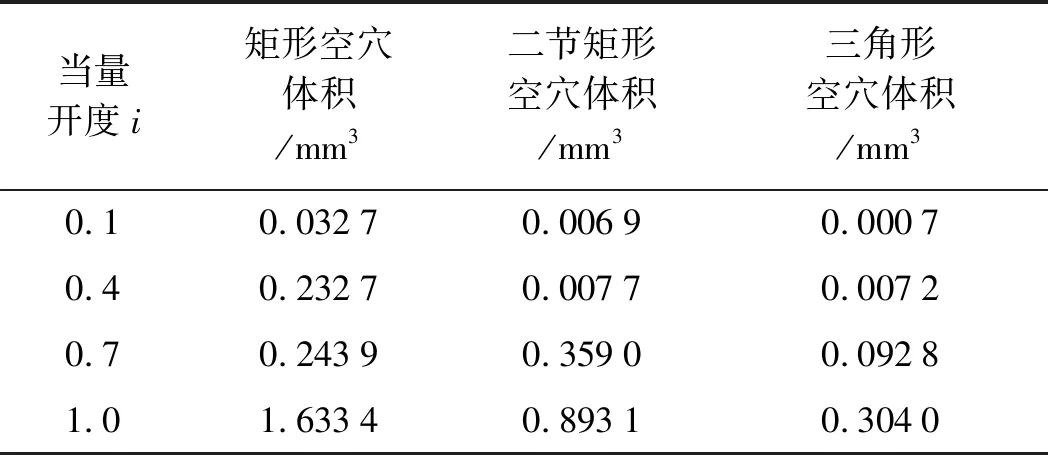
表3 气体体积表

表3显示:当量开度越大,气体体积越大时,空穴现象越明显;在同一开度下,矩形阀口空穴体积最大,三角形阀口空穴体积最小;

全开状态下矩形阀口结构气体体积为1.633 4 mm3,二节矩形阀口结构气体体积为0.893 1 mm3,三角形阀口结构气体体积为0.304 0 mm3。

4.2 流量特性

上文分析了两相流模型下3种阀口压力分布情况以及空穴体积大小。接下来,笔者在两相流的基础上,分析不同阀口结构下比例阀的流量特性,通过对比实验结果的方式,以此来验证仿真的结果。

计算收敛后,笔者统计监测位置流量数据,并使用Origin软件绘制了其流量特性曲线。不同当量开度下,3种阀口结构的流量如图6所示。

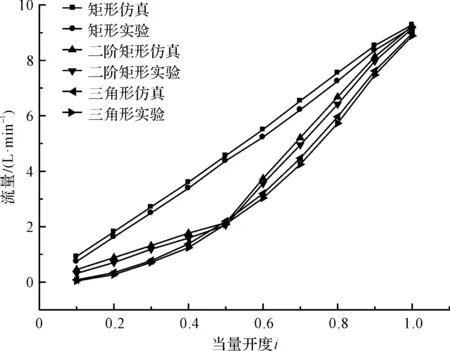
图6 流量特性曲线

图6中,阀口形状决定了阀的流量曲线特点,并且3种阀口结构对应3种流量曲线特点,3种曲线相同的特点都随着当量开度增大,3种阀口结构的流量随之增大。

从图6所示的矩形阀口仿真流量曲线可知:矩形阀口流量呈线性关系,这是因为矩形阀口随着当量开度的增大,阀口面积呈线性增大,阀口面积与当量开度的关系如式(8)所示;根据矩形阀口流量特性曲线的特点,该结构阀口易线性控制流量,电磁阀易调控阀流量。

从图6所示的二阶矩形阀口仿真流量曲线可知:曲线近似为两段直线,在阀芯当量开度为0.5曲线发生偏折,小位移流量曲线斜率较小,大位移流量曲线斜率较大。这是因为二阶矩形阀口在当量开度0.5位置处,阀口的宽度发生变化,从式(9)可以得到在当量开度小于0.5时,阀口面积与当量开度成正比,当量开度大于0.5时,阀口面积与当量开度为一次函数关系,一次函数的斜率为正比例函数斜率的3倍,二阶矩形阀口面积变化的情况决定了流量曲线特性。在0.5当量开度,阀口面积迅速增大,在该位置流量曲线斜率变大。该流量曲线可以在小当量开度线性控制比例阀小流量,大当量开度比例阀流量响应迅速。

从图6所示的三角形阀口仿真流量特性曲线可知:曲线近似为抛物线,随着阀芯位移的增大,流量曲线斜率在增大。这是因为三角形阀口的面积与当量开度的平方成正比,如式(10)所示;随着当量开度的增大,阀口面积呈抛物线增长,因此流量特性曲线近似为抛物线。

为了验证上述仿真结果的准确性,笔者采用比例阀性能实验台,分别对3种阀口结构比例阀进行测试,通过改变电流的大小控制其电磁力,控制着阀口开度的大小。实验比例阀进出口压力与仿真保持一致,实验完成后笔者将比例阀流量实验数据绘制成曲线,把实验曲线与仿真曲线作对比。

对比结果可知:仿真曲线高于实验曲线,这是因为数值仿真模型清除了一些圆角和拐角,模型表面做了理想化处理,减少了流阻。但3种阀口的仿真曲线和实验曲线变化趋势相同,曲线近似重合。

通过仿真与实验结果的对比,验证了仿真结果的可靠性。

笔者通过对比3种阀口结构的流量特性曲线,得到在当量开度为1时,矩形和二阶矩形流量近似相等,三角形阀口流量较低。矩形阀口流量曲线较高,具有流量线性控制的优势。二阶矩形阀口流量具有在阀口小当量开度易实现低流量线性控制,在大当量开度易实现高流量响应迅速的优势。三角形阀口具有可实现比二阶矩形小当量开度更小流量控制的优势,但是不能实现流量的线性控制。

流量系数反映了阀口的节流特性,流量系数越大,阀口的节流损失越小。当量开度下3种阀口结构的流量系数曲线如图7所示(曲线反映了不同阀口结构流量系数的变化情况)。

图7 流量系数曲线

图7中,当量开度小于0.5,矩形阀口流量系数较高,二阶矩形阀口流量系数次之,三角形流量系数最小。这是因为阀口当量开度范围为0～0.5时,矩形阀口的面积最大,流体节流损失较小,三角形阀口的阀口流体节流损失最大,流量系数最低。

而当量开度范围为0.6～1时,二阶矩形阀口流量系数较高,矩形阀口流量系数次之。这是因为在当量开度大于0.5,二阶矩形阀口相对于矩形阀口逐渐变宽,流体流动损失减小,流量系数变大。

从3种不同结构阀口流量系数对比分析可知:小开度下矩形阀口节流损失较小,流量系数较大。大开度下二节矩形阀口节流损失较小,流量系数较大。与前两者相比,三角形阀口的节流损失最大,流量系数最小。若从阀口节流损失角度考虑来进行结构设计,应选取矩形或者二阶矩形阀口。

在液压工程机械控制系统中,比例阀应用广泛,例如船用大型柴油机柱塞油泵、车辆工程大功率柴油机等。比例阀控制柴油进油量,低工况需要比例阀在小当量开度精准控制小流量,高工况需要比例阀在大当量开度控制流量快速响应。

综合仿真实验过程可知,3种阀口结构空化气体体积对流量特性曲线影响不大。

三角形阀口在小当量开度流量最小,但是不能实现流量的线性控制,阀口节流损失较大,流量系数较小,因此比例阀阀口设计不建议采用该结构;

二阶矩形相比矩形阀口,更能实现低工况线性准确控制流量,高工况大流量迅速响应,因此二阶矩形阀口更适合应用于大型柴油机柱塞泵。

5 结束语

笔者基于CFD两相流空穴模型,结合仿真和实验对比分析的方法,分析了比例阀不同阀口结构下的流动特性,研究结论具体如下:

(1)3种结构的压降主要发生在阀口位置,该位置发生空穴现象,矩形阀口空穴体积最大,三角形阀口空穴体积最小。较小的空穴体积对流量特性影响不大;

(2)仿真与实验流量特性曲线趋势相同,验证了仿真的准确性。阀口结构影响比例阀流量特性曲线,矩形阀口流量呈线性变化,二阶矩形阀口流量呈两段线性变化,三角形阀口流量呈抛物线变化;

(3)三角形阀口流量系数最低,低工况下矩形流量系数较大,高工况下二阶矩形流量系数较大。从节流损失角度来看,不建议采用三角形阀口的设计。

综合笔者研究过程可知,与矩形阀口相比较,二阶矩形更能实现在低工况线性准确控制流量,高工况大流量迅速相应。

因此,二阶矩形阀口更适合应用于大型柴油机柱塞泵,该结果为后续比例阀节流口对阀芯瞬态液动力影响的研究奠定基础。