属性权重未知情形下的q阶orthopair犹豫模糊TOPSIS法
金 贵,周礼刚,吴 澎,刘欣悦
1.安徽大学 数学科学学院,合肥 320601
2.安徽大学 商学院,合肥 230601
多属性决策问题是现代决策科学中重要的一部分。在决策过程中,因为决策问题的复杂性和决策环境的不确定性,决策者很难用确定的数值去表达相关的决策信息。为此,Zadeh[1]提出了模糊集。在多属性决策问题中,模糊集可以用来表征决策者不确定的决策信息。但在一些情况下,很难仅用一个数值去定义隶属度。为了克服模糊集这一不足,Torra[2]对模糊集进行了拓展,并提出了犹豫模糊集。犹豫模糊集包含若干个在[0,1]内的数值,用来表示隶属度。但是,模糊集和犹豫模糊集只有隶属度没有非隶属度。基于此,Atanassov[3]提出了直觉模糊集(IFS),其隶属度μ和非隶属度ν满足μ+ν≤1。然而,Yager[4]认为IFS表示的信息范围是有限的,并提出了q阶orthopair模糊集(q-ROFS),其中隶属度μ和非隶属度ν满足μq+νq≤1。如果q=1,q-ROFS退化成IFS。随着q值的增大,可以表示更大范围的模糊信息。本文在充分结合犹豫模糊集和q-ROFS优点的基础上,提出了q阶orthopair犹豫模糊集(q-ROHFS),并将其运用于决策过程中,以弥补上述模糊集理论的缺陷。
自从犹豫模糊集和q-ROFS相继提出,它们受到了越来越多的学者的关注[5-9]。例如,文献[10]提出了基于灰色关联度分析的犹豫模糊多属性决策方法。文献[11]提出了一种基于正交投影法的犹豫模糊多属性决策方法,并应用在军事训练方面。文献[12]提出了一种改进的犹豫模糊加权平均算子,并基于犹豫模糊决策算法建立了云制造系统选择模型;文献[13]研究了直觉犹豫模糊集的加权距离测度,并基于该测度提出了TOPSIS决策方法。文献[14]给出了基于直觉犹豫模糊集知识测度的多属性决策方法,并将此方法应用到某互联公司的空调安装公司选择的案例中。文献[15]基于线性比例法提出了一种广义犹豫模糊决策矩阵的规范化方法,并发展了一种广义犹豫模糊动态TOPSIS评价模型;文献[16]基于q-ROHFS的基本运算,构建了q阶orthopair犹豫模糊多属性群决策模型。文献[17]提出了基于q-ROHFS的新的距离测度,并利用该测度提出了TOPSIS多属性决策方法,并应用在能源问题中。
属性权重的确定是决策过程中一个重要问题,赋权方式是否科学直接影响评价的最终结果。基于上述文献综述可知,大量工作主要集中研究了属性权重已知的q阶orthopair犹豫模糊多属性决策问题。同时,鲜有文献考虑了决策信息之间的联系。因此,避免主观赋权的不足,有必要对这方面进行研究。本文首先简要地回顾一些有关犹豫模糊集、q-ROFS和q-ROHFS的概念以及q-ROHFS的运算法则。其次,基于q-ROHFS的概念,提出基于Theil不等系数的加权距离测度,并基于该距离测度,构建以离差最大化为目标的属性权重确定模型。基于以上工作,提出一种新的TOPSIS多属性决策方法。最后,将该多属性决策方法应用到能源方案挑选问题中,并对参数q进行灵敏度分析以及将该方法与现存多属性决策方法进行比较分析。
1 预备知识
定义1[17]设X={x1,x2,…,xn}为论域,称H={<xi,h(xi)|xi∈X>}为X上的犹豫模糊集,其中h(xi)表示X的元素xi属于H的所有可能隶属度组成的集合。
记h={h1,h2,…,hl}为犹豫模糊数,且满足条件0≤hi≤1,hi≤hi+1。
定义2[17]设X={x1,x2,…,xn}为论域,称Q={<xi,(μQ(xi),νQ(xi))>q|xi∈X}(q>1)为X上的q阶orthopair模糊集(q-ROFS),其中μQ:X→[0,1],νQ:X→[0,1]是X上的模糊集,μQ(xi)、νQ(xi)表示xi属于Q的隶属度和非隶属度,且有0≤μqQ(xi)+νqQ(xi)≤1。


2 新的q阶orthopair犹豫模糊距离测度
设Qj={Qj(xi)|xi∈X}∈q-ROHFS,Qj(xi)=Qji=<hQj(xi),gQj(xi)>q∈q-ROHFS,i=1,2,…,n,j=1,2,由于在一般情况下,Q1和Q2中的q阶orthopair犹豫模糊元素的长度不等,即l(hQ1(xi))≠l(hQ2(xi)),l(gQ1(xi))≠l(gQ2(xi))为了能够比较Q1和Q2,需要对它们进行扩充,使得它们的长度相等。
定义6[18]设#M、#N分别为l(hQj(xi))、l(gQj(xi))的最小公倍数,则Qji可扩充成:



其中,q≥1,k1=1,2,…,#M,k2=1,2,…,#N。
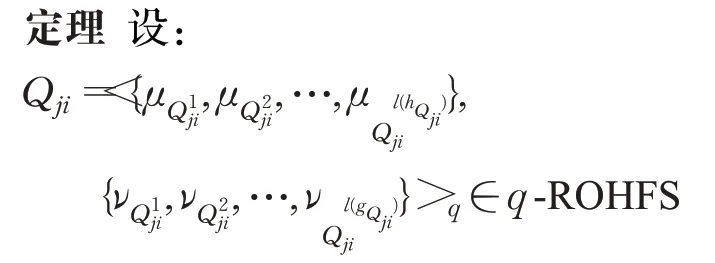
j=1,2,3,则基于Theil不等系数的q阶orthopair犹豫模糊集的加权距离测度d(Q1,Q2)满足以下性质:
(1)0≤d(Q1,Q2)≤1;
(2)d(Q1,Q2)=d(Q2,Q1);

证明

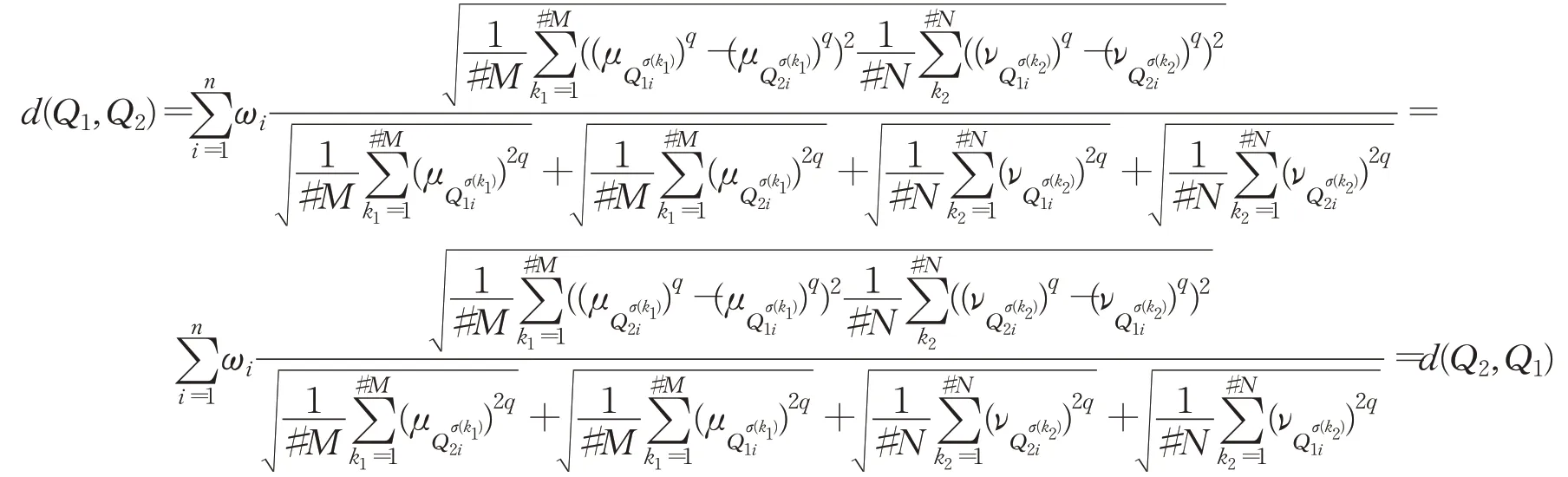
(3)根据定义7可得:
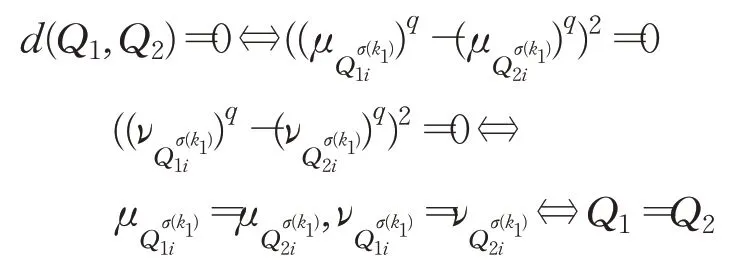
3 q阶orthopair犹豫模糊TOPSIS法
在q阶orthopair犹豫模糊决策矩阵A=(Aji)m×n=(<hAj(ci),gAj(ci)>q)m×n中,对于属性ci而言,决策方案Aj与其他方案At之间的基于Theil不等系数的q阶orthopair犹豫模糊集的加权距离测度用Dji(ω)表示,可定义为:

其中,i=1,2,…,n,j,t=1,2,…,m,k1=1,2,…,#M,k2=1,2,…,#N。
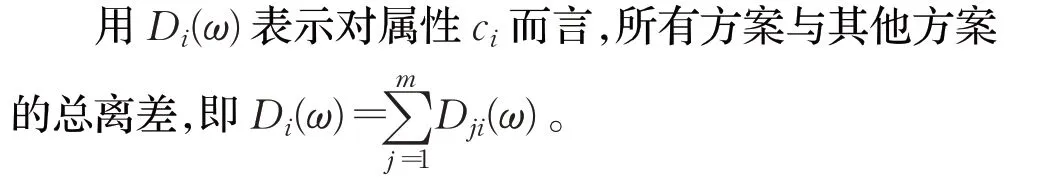
多属性决策,一般是对这些方案综合属性值的排序进行比较。因此,对方案属性值偏差越大的属性应该赋予越大的权重。
在q阶orthopair犹豫模糊信息环境下,属性权重的选择应使所有属性对所有决策方案的总离差最大。基于该思想和文献[19]的启发,为了求解属性权重,构建了如下最优化模型:
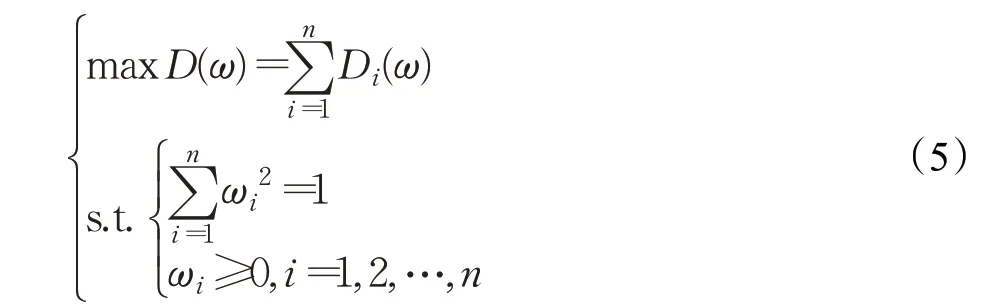
其中:

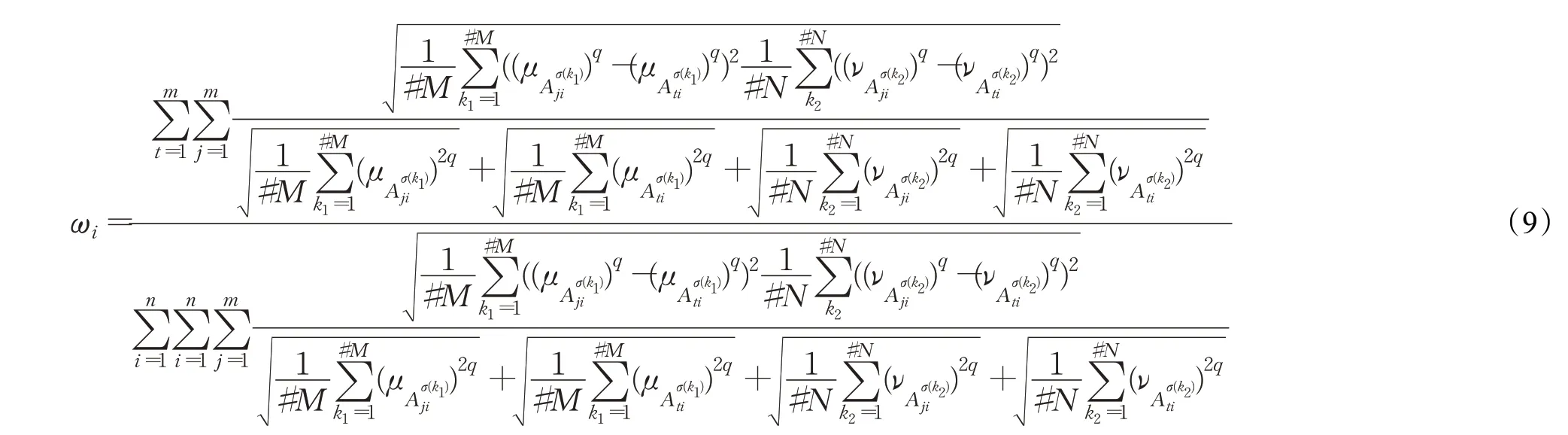
针对q阶orthopair犹豫模糊多属性决策问题,提出基于新的距离测度的TOPSIS多属性决策方法,具体步骤如下:
步骤1分别计算l(hAj(ci))、l(gAj(ci))的最小公倍数为#M、#N(i=1,2,…,n,j=1,2,…,m),将原始q阶orthopair犹豫模糊集矩阵A进行规范化处理,规范化后的矩阵为A*,可表示为

步骤3通过求解模型式(5)可得属性权重向量ω=(ω1,ω2,…,ωn)T。
步骤4根据公式(3),计算各方案Aj到A+、A-的基于Theil不等系数的q阶orthopair犹豫模糊集的加权距离:

4 q阶orthopair犹豫模糊TOPSIS法的应用
当今世界,能源发展问题已经成为许多国家共同的话题。文献[17]提出,为了全面、客观地评判能源方案,应从经济c1、科技c2、环境c3、社会政治c4等4个方面进行综合评价。假设现有5个能源方案Aˉ={A1,A2,A3,A4,A5},专家组根据自身的知识、经验以及已有的统计数据确定出每个能源方案Aj(j=1,2,3,4,5)关于属性ci(i=1,2,3,4)的q阶orthopair犹豫模糊评价信息Aji,得到的q阶orthopair犹豫模糊决策矩阵A=(Aji)5×4,如表1所示[17]。

表1 q阶orthopair犹豫模糊决策矩阵Table 1 q-rung hesitant fuzzy decision making matrix
步骤1分别计算l(hAj(ci)),l(gAj(ci))的最小公倍数为#M=12,#N=6(i=1,2,…,n)将原始q阶orthopair犹豫模糊集矩阵A进行规范化处理,规范后的矩阵为A*,则拓展后的决策矩阵为A*=(Aji*)5×4,其中:



步骤3求解模型(5)得到属性权重向量:ωi=(ω1,ω2,ω3,ω4)T=(0.216 2,0.245 5,0.286 3,0.252 1)T
步骤6根据步骤5可得η5>η4>η3>η1>η2。易知A5>A4>A3>A1>A2,即A5是最优的选择方案。
以下将讨论参数q对基于Theil不等系数的q阶orthopair犹豫模糊集的加权距离测度对决策过程的影响。图1描述了参数q对各属性权重的影响。图2描述了参数q对各方案综合评价值的影响。从图1可以看出,随着q的增大,ω1不断地增大,ω2先减小后增大,ω3先减小后趋于平稳,ω4先增大再减小后趋于稳定,虽然各属性权重变化趋势不同,但受距离测度的影响不断减弱,逐渐趋于平稳。图2表明随着q的不断增大,η1和η3先增大后趋于稳定,η2未受太大的影响,η4和η5先减小后趋于稳定,可以看出,无论参数q的取值怎样变化,方案的排序结果没有发生大变化。即方案5始终是最佳方案。

图1 参数q对ωi的影响Fig.1 Influence of q onωi

图2 参数q对ηj的影响Fig.2 Influence of q onηj
最后将验证基于Theil不等系数距离的确定属性权重的TOPSIS决策方法的优越性和有效性,首先用直觉犹豫模糊集(IHFS)代替q-ROHFS表示决策信息,它是q-ROHFS在q=1时的特殊情况,但是会发现有些决策信息不能被表示,比如上述案例中A1关于属性c1的评估值为<{0.3,0.4,0.5},{0.7,0.8}>q,其包含的隶属度0.5与非隶属度0.7之和大于1,从而体现了q-ROHFS的优越性。接着与文献[17]提出的基于q阶orthopair犹豫模糊广义加权距离测度的多属性决策方法进行比较,发现两种方法有着相同的排序结果,进一步说明了本文提出方法的有效性。相较于文献[17]提出的决策方法,本文提出了一种新的距离测度,除此之外,文献[17]的属性权重是给定的,而本文通过属性权重模型将其定量化,更好地利用了数据之间的联系,从而提供了更加客观的过程。基于相同的决策信息和信息测度,文献[20]利用得分函数和精确函数对方案进行排序择优,相较之下,本文采用的新TOPSIS法能充分运用原实时数据的信息,其结果能精确地反映各方案之间的差距。以上与现存多属性决策方法的对比,更能凸显出基于Theil不等系数距离的确定属性权重的TOPSIS决策方法的优越性。
5 结束语
多属性决策是一个很重要的实际问题,它最基础、最重要的研究方向是如何表达这些模糊信息。IHFS和PHFS均是处理模糊信息的好方法,然而,q-ROHFS适用范围更广,即μq+νq≤1,IHFS和PHFS都是它的特殊情况。因为q-ROHFS有参数q,所以它可以更灵活地表示信息,展现的空间范围更广。
基于这些优点,首先提出了基于Theil不等系数的q-ROHFS的距离测度,并讨论了它的性质。其次,提出了基于Theil不等系数距离的属性权重确定模型,用来更客观地确定属性权重。基于上述研究,提出了一种新的TOPSIS多属性决策方法。最后,通过实例与比较分析说明了该方法的可行性和有效性。
新的多属性决策方法的优点总结如下:(1)因为提出的方法包含参数q,所以可以容易地反映出决策者的风险偏好;(2)从总离差最大化的原则出发,提出了基于单目标优化模型的属性权重确定模型,使得决策过程更具有说服力。
在未来的研究中,致力于提出基于q-ROHFS其他信息测度。同时,也会将提出的方法运用到其他领域。例如物流管理、风险评估和医疗诊断[21]等。

