异构大数据环境中高效率知识融合方法的研究

汪 玉，王 鑫，张淑娟，郑国强，赵 龙，郑高峰

1.国网安徽省电力有限公司 电力科学研究院，合肥 230601

2.国网安徽省电力有限公司，合肥 230022

Web 3.0与大数据时代的到来证实了多种前期技术理论的实践与应用可行性，谷歌公司在2012年提出的“知识图谱”就是其代表性实例之一[1]。大数据环境中，知识图谱通过结合不同个体的关系、属性可视化模型与语义网技术，可使复杂的异构应用实现便捷、高效的人机信息交互。作为多种现代技术的结合，知识图谱的核心技术包含智能语义[2]、知识提取[3]、知识关联[4]、知识融合[5]、知识加工[6]等。其中，知识融合通过利用知识推理[7]、实体/本体匹配[8]等技术途径，从不同数据源、不同数据结构的大数据环境中提取、关联、合并同义或近义知识，从而实现异构知识图谱的信息交互及协作应用。

知识融合是知识图谱的关键环节，也是支撑知识图谱可用性的重要要素，其核心为实体的消歧[9]与对齐[10]。实体的消歧指大量数据中同义实体的抽取及分类，一般用于海量异构数据的知识提取及知识分类；实体的对齐指同义、近义的实体或属性间相互关系的分析，一般用于复杂异构实体的知识映射。实现实体的消歧与对齐通常采用基于机器学习技术的自然语言处理，从大量的半结构化数据中分析、提取近义实体，对齐、映射相关属性。机器学习算法主要分为监督学习算法和无监督学习算法。监督学习算法（如贝叶斯估计、支持向量机等）使用历史数据样本训练数据分析模型，通过数据预测、数据聚类等途径进行实体对齐及属性融合，具有较高的实时性，但较依赖于历史数据样本；无监督学习算法（如主成分分析、人工神经网络等）无需样本训练成本，但一般复杂度较高，尤其在多维、异构的大数据环境中较难满足知识融合的实时性。

据此，本文面向多维、异构的复杂大数据环境，提出一种结合监督学习、概念漂移检测以及无监督反向验证的高可靠、低复杂度知识融合方法。一方面，在监督学习过程中，该方法采用贝叶斯估计算法训练历史数据模型，预测待对齐实体，并周期性利用孤立深林算法检测、修正概念漂移数据样本，提高历史数据模型的可靠性；另一方面，在反向验证过程中，该方法采用一种低复杂度自组织映射（self-organizing map，SOM）神经网络算法，分析实体歧义并根据评估结果实时调整监督学习的权重系数，进一步提炼数据模型，加强知识融合的准确性。

本文提出方法在公开数据集及国网安徽省配电网知识图谱系统中进行了多项对比实验。实验结果表明，提出方法在历史模型训练、知识融合效率、算法复杂度等方面均优于常规机器学习算法。

1 知识融合技术相关研究

随着知识图谱在各行各业的迅速普及，跨业、跨界数据的知识融合技术已然引起了学术界的广泛关注。国内方面，刘峤等[11]详细解释了知识融合的概念、意义及知识融合在知识图谱应用中的重要性；于梦月等[12]分析了现代知识融合的支撑理论架构，在知识融合的各阶段列举了多种知识融合理论模型；高国伟等[13]具体分析了先网络环境的碎片化知识特征，提出了一种结合非线性融合模型的知识超网络的融合框架；侯位昭等[14]针对解决推荐服务的信息爆炸问题，通过在推荐服务提出了一种基于贝叶斯网络模型的知识图谱融合技术；程秀峰等[15]面向用户行为数据的采集与共享应用，在科研数据管理系统中通过知识融合技术分析了科研工作者的行为数据共享机制，并通过开发、应用移动行为数据采集APP开展了实证研究。异构数据的知识融合是现代知识图谱技术的关键应用，常用于多语言知识链接、融合等，余圆圆等[16]面向跨语言百科文章之间的知识融合应用，提出了一种结合双语主题模型及双语词向量的候选集排序模型，实现了中英文维基百科间的知识链接；余传明等[17]提出了一种基于机器学习，融合双语词嵌入的主题对齐模型，通过提出双语主题相似度、双语对齐相似度等新对齐指标，改进了传统双语主题模型的语义共享；赵生辉[18]针对建模藏汉双语融合型知识图谱，通过从逻辑框架、知识模板和数据实例等三个层面解析建模原理，实现了多语言知识图谱的创建及跨语言知识检索。

国际方面，Ruta等[19]针对车载自组织网络的上下文信息共享问题，提出了一种基于非标准、非单调推理服务的知识融合算法，实现了车载网络节点不一致上下文注释的自动协调及合并；Huang等[20]针对多源区间值（Interval-Valued）数据的动态融合，提出了一种将多源区间值数据转换为梯形模糊颗粒的模糊信息融合方法及增量分析算法；Sultana等[21]面向基于社交行为提示的生物识别应用，通过融合个人知识、社交行为知识和独有生物特征，增强了传统生物识别系统的性能；Liu等[22]分析了基于知识图谱的专家系统、搜索引擎及知识问答系统在害虫及作物病害的应用，介绍了知识图谱的知识融合技术在智慧农业的应用现状；Han等[23]针对电力设备电源质量问题的多样性及复杂性问题，提出了一种基于知识-数据融合的神经网络模型，在常规信息、质量信息、过程信息等异构数据中有效提高了电源质量问题的分析效率；Li等[24]面向异构知识图谱的融合应用，提出了一种基于图结构数据、图神经网络，用于融合知识图谱实体子图结构的知识融合机制，实现了知识图谱中实体的融合嵌入。

2 本体模型

本文提出的算法针对大数据环境中异构、半结构化数据的知识融合，因而采用了基于实体对齐的本体映射方法。本体（Ontology）在信息学科中，是一种对于数据的抽象概念模型，是人类与智能设备间存在的概念模式以及互交模式的形式化描述[25]。本体的建模以及匹配是大数据环境中实现知识共享、知识重用的关键要素。

本文采用了较为通用的本体模型，由实体、关系、属性三元组组成，如式（1）定义：

其中，O为本体，E为实体（Entity），R为关系（Relation），A为属性（Attribute）。实体、关系为结构化数据。其中，实体是本体的固有识别名，可以是物体、状态、现象等对象的名称，相同实体在异构数据库中可对应不同本体；关系是本体中实体所对应属性的关联规则的集合。实体、关系在同构数据集中具有同等的定义，但在异构数据集间存在潜在的歧义。属性为非结构化数据，包含实体由关联规则对应的其他实体与对应关系的集合，由式（2）描述：

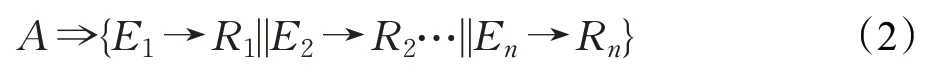
总之，本体模型中各元组的相互关系如图1所示。

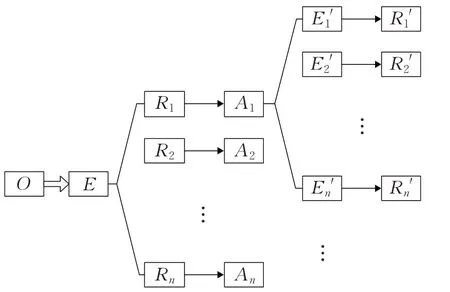
图1 本体模型关系图示例Fig.1 Example of relationship diagram of ontology model

即本体中唯一的E通过R关联A，而A为非结构化自然文本数据，可包含多项其他E′及R′的关联。该模型为二维本体，可根据应用需求及数据的信息量进一步扩展多维本体。

3 基于概念漂移检测的监督式知识融合

根据上述本体模型，分析本体的相关度，进行基于贝叶斯估计法的实体对齐，通过映射相关属性，实现知识融合。该过程的输入为一个待融合本体；分析对象为目标数据库中具备相同或近义实体的本体，近义实体则通过常规的文本相似度分析法进行判断；输出为目标数据库中相关度最高的本体集。目标本体与待融合本体的相关度F(O)的计算方法有如式（3）所示：

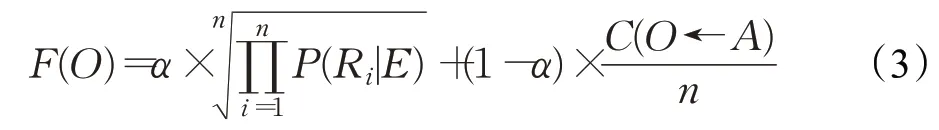
其中，O为异构数据库中与待融合本体存在相同或近义实体的本体，取决于实体名称的文本相似度；α为权重系数，默认值为0.5，根据反向验证结果持续更新，在后续章节详细叙述；n为相同或近义实体的数量；C(O←A)为目标本体与待融合本体的属性相关度，有如式（4）所示：

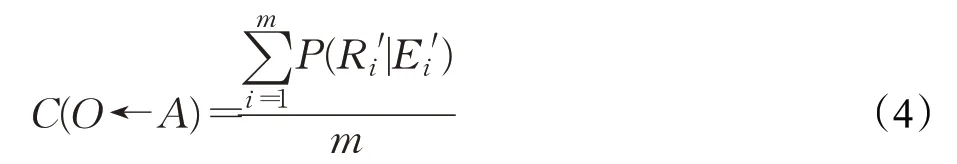
其中，m为本体O所包含属性的数量；P(R|E)为贝叶斯后验概率，由下式得出：

其中，P(R,E)、P(E)为先验概率，从数据库中统计得出；考虑到R之间无直接相关性，式（3）由后验概率的平均值估算属性相关度。

据此，通过计算本体间相关度，提取与待融合本体得出较高相关度的本体集合，对齐实体并连接相关属性，实现异构数据库的知识融合。如上公式，基于贝叶斯估计的相关度分析需充分利用历史数据模型，统计实体与关系的先验概率。而实际应用中，异常、突发事件的发生（如因突发事件，特定实体、关系的出现频度骤增）可导致历史数据的偏移，触发概念漂移[26]，从而降低贝叶斯数据模型的可靠性，如图2。

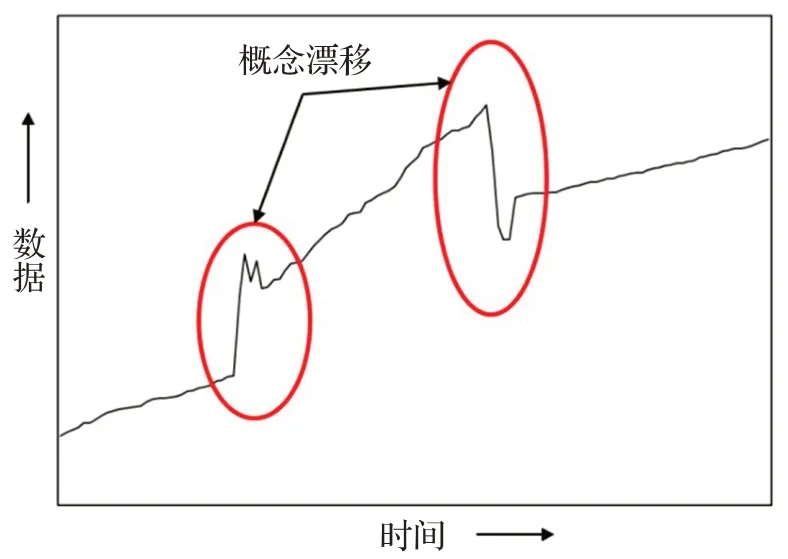
图2 概念漂移示意图Fig.2 Example of concept drifting

据此，采用基于孤立森林（iForest）的异常点检测算法，进行概念漂移的检测及数据模型的修复。该过程的具体目标为检测、聚类非预期数据，并将其拟合至常规数据模型，提高整体历史数据模型的可靠性，具体如下。

首先，在历史数据中选择定量样本，构建决策树（iTree）；随后，按均匀分布提取少量检测点，计算检测点在每棵iTree的平均高度h；最终，遍历所有iTree，计算检测点的异常概率分值，如式（6）：

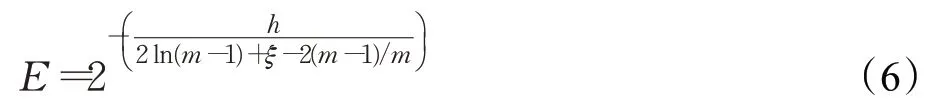
其中，E为0～1之间的异常概率分值；m为样本个数；ξ为欧拉常数。

由上式，设定异常阈值，将异常概率分值大于异常阈值的数据判断为异常数据。该过程中，离散的异常数据仅视为异常事件，从数据库隔离；而连续的异常数据则判断为概念漂移，将第一个异常数据的位置设定为概念漂移的起点，最后一个为终点，对范围内的所有数据（包括非检测点数据）进行历史模型的拟合，如式（7）所示：

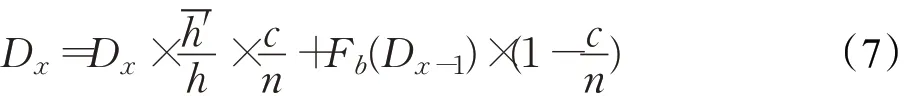
其中，Dx为第x个概念漂移数据；′为概念漂移数据在iTree的平均高度；c为概念漂移范围的异常数据总量；n为发生概念漂移前历史数据的总量；Fb为概念漂移前贝叶斯模型的预测函数。由上式，概念漂移的修正取决于异常数据的数据量及偏移量，异常数据量较多，其拟合过程偏向于数据偏移量的大小，反之，则偏向于贝叶斯历史数据模型。

4 基于自组织映射的无监督式反向验证

多维、异构的数据库中，实体名称的歧义可导致历史数据模型的分析误差，而反向验证是进行实体消歧，提炼数据模型的有效手段。本文提出一种基于自组织映射（SOM）神经网络的反向验证算法，分析已对齐实体的歧义，辅助提高知识融合过程的知识融合准确率。该算法通过逆向匹配由贝叶斯数据模型对齐的实体集，进行实体的歧义补正，进一步提炼历史数据模型的可靠性。

SOM是一种竞争型、无监督式神经网络，常用于数据聚类[27]、协同控制[28]等。该神经网络中，各神经元通过竞争、聚类、加权过程的多次迭代，实现复杂的信息处理。本文的反向验证过程中，输出神经元对应异构数据库的所有实体，输入神经元对应待匹配实体，而竞争过程则对应神经元在异构数据库间的匹配度比较过程。

提出的反向验证算法通过SOM的无监督式迭代匹配，评估已融合本体中各实体相似度，进行监督式本体融合的权值更新。首先，以首个数据库的已对齐实体为输出神经元，待匹配数据库的所有实体为输入神经元，进行匹配度比较并选择获胜神经元，如图3。

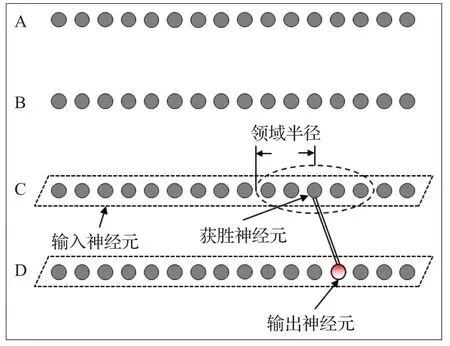
图3 基于SOM的反向验证算法（首次迭代）Fig.3 SOM-based reversing verification algorithm（first iteration）

图3中，数据库的迭代顺序由已融合本体的相关度F(O)（式（1））排序而定。获胜神经元选择过程如式（8）：

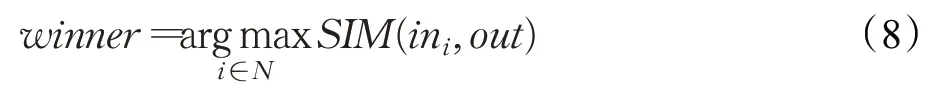
其中，winner为获胜神经元，i为输入神经元编号；N为输入神经元集合；in为输入神经元；out为输出神经元；SIM为实体匹配度，由式（9）得出：

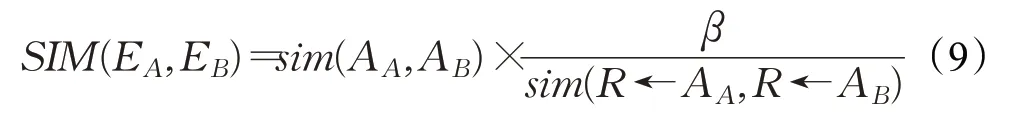
其中，E为比较本体所对应的实体；sim为文本相似度；AA、AB为两个比较实体所对应的属性中，具备最高文本相似度的属性；R为关系，R对应该属性与相关实体；β为匹配度权值，取决于已融合本体与获胜神经元的本体相关度F(O)。

下一步为基于SOM规则的近义实体聚类过程。以上一次获胜神经元为中心，计算SOM领域函数，如式（10）：

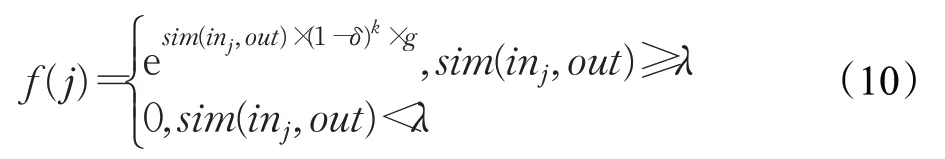
其中，j为输入神经元编号；δ为0到1的常数，根据数据库间的相关性设定；k为迭代次数；g为最高匹配值；λ为领域半径。由此，下一轮迭代的输出神经元为获胜神经元的领域半径(λ)内的所有本体，输入神经元为数据库C的所有本体，而领域值(f)则决定各输出神经元的匹配权值，获胜神经元获得最高权值，其他神经元与获胜神经元越近，则获取更高的权值，首次迭代结束。

再次进行迭代竞争，与首次迭代不同，此时的输出神经元为所有领域半径内的神经元，匹配度比较公式更新如下：

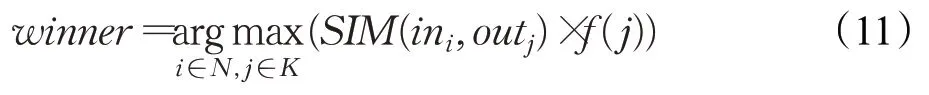
其中，j为输出神经元编号；K为输出神经元集合；f为匹配权值。

由式（11），选择该轮迭代的获胜神经元，如图4。图中，上轮的获胜神经元具备最高的匹配优先度，但在数据库B中找出最高匹配度本体的神经元是领域内其他神经元。因而，本轮获胜神经元为数据库B中与该最高匹配度本体所对应的神经元。

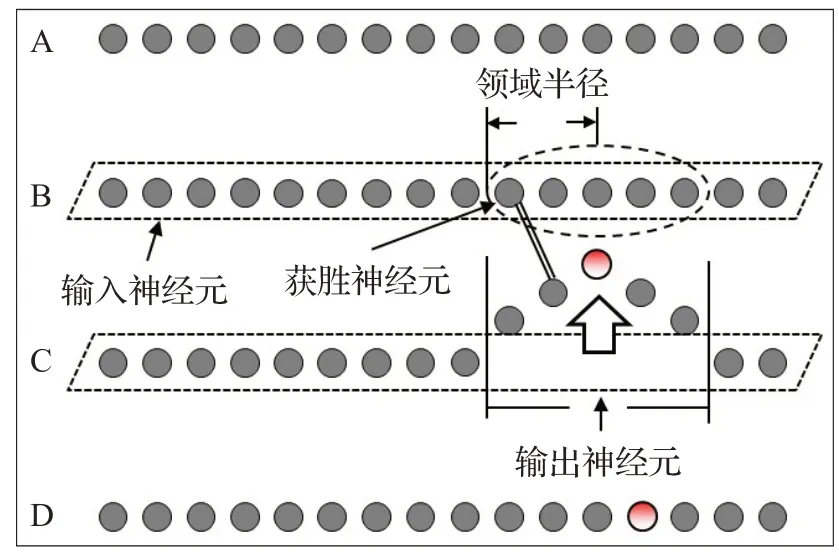
图4 基于SOM的反向验证算法（二次迭代）Fig.4 SOM-based reversing verification algorithm（second iteration）

持续迭代该过程，直到在所有异构数据库中选出获胜神经元，如图5、图6。

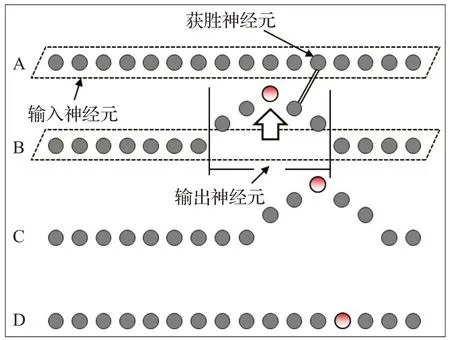
图5 基于SOM的反向验证算法（最终迭代）Fig.5 SOM-based reversing verification algorithm（last iteration）

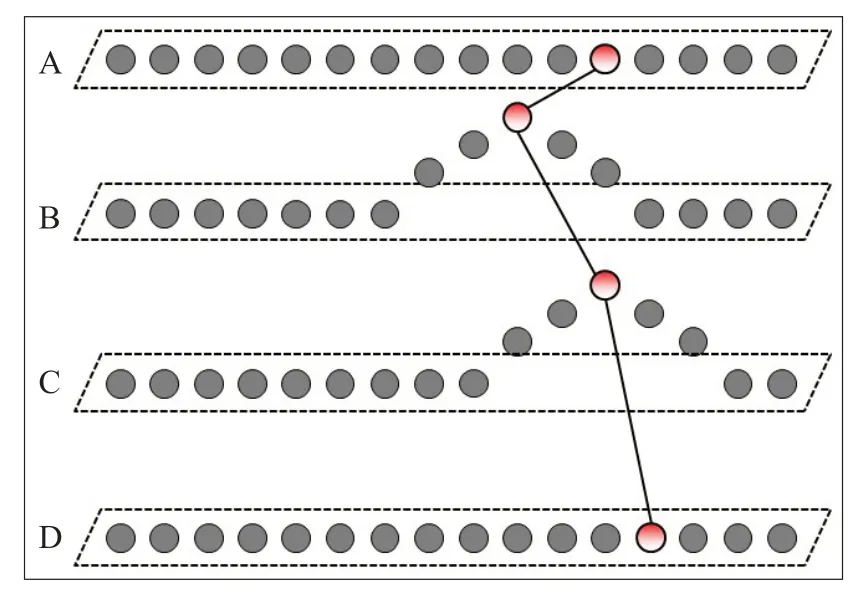
图6 提取获胜神经元Fig.6 Extracting winner neurons

最终，通过已融合本体与获胜神经元的相似度比较，更新监督式知识融合的权重系数α（式（3）），如式（12）所示：

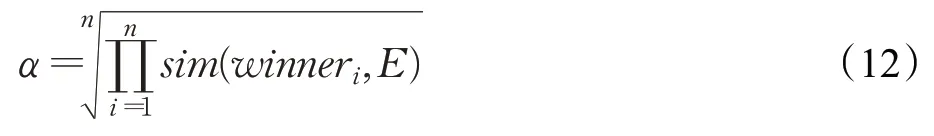
其中，n为SOM神经网络的迭代次数。

基于SOM神经网络的反向验证算法无需在数据库中获取先验知识，且相比常规的无监督式神经网络算法，在每轮迭代过程中仅在获胜神经元领域半径内进行神经元比较，从而大幅度降低了神经网络的拓扑结构复杂度，并保证了算法的收敛性。

5 性能分析与评价

通过在多维、异构数据环境中进行对比实验，分析了提出方法的知识融合效率以及应用可行性。

首先，利用加利福尼亚大学机器学习与智能系统中心的公开数据集[29]，对监督学习、概念漂移检测、无监督反向验证等提出方法的三阶段运作过程进行了比较分析。该数据集包含了2014—2017年北京市天坛、奥体中心、万柳、昌平等12个区域的空气质量、温度/露点温度、风向/风速、空气压强、降雨量等时序性环境数据。

第一阶段实验的分析对象为提出方法的概念漂移检测算法在贝叶斯历史数据模型的数据预测效率。预测对象为基于PM2.5值的某区域空气质量。实验中，使用30%的数据构建了贝叶斯历史数据模型，随后在剩余70%数据种随机删减30%的数据，对删除的数据进行了基于贝叶斯估计的数据预测，实验结果如图7所示。可以看出，基于概念漂移检测算法预测的数据分布与实际历史数据分布的吻合度相比于传统贝叶斯监督学习显著高，由此说明结合概念漂移监测算法，可以通过检测、修正概念漂移数据提高数据预测的准确率，进而提高历史数据模型的可靠性。

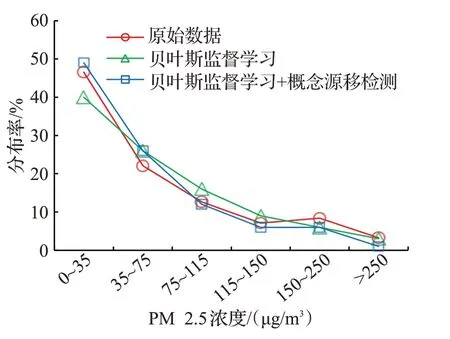
图7 原始样本分布与预测数据分布的比较Fig.7 Comparison of distributions of original samples and predicted data

第二阶段实验为整体方法的实体对齐效率。该阶段将17种风向与10类风速组合文本设定为“实体”，温度的特定区间设定为“关系”，其他对应数据（不包含时序数据）为“属性”，以对齐实体的时间相关度差值为融合指标，进行了12个数据集的本体融合。实验结果如图8。

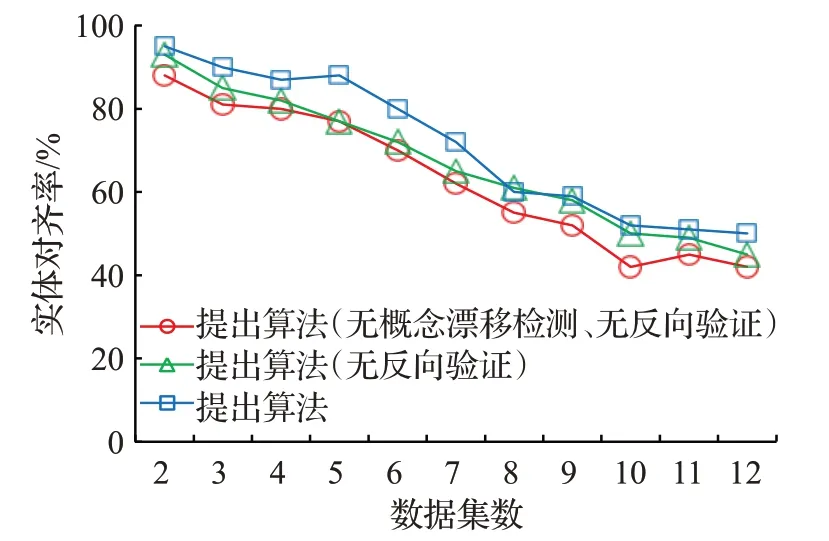
图8 融合率比较Fig.8 Comparison of fusion rate

实验比较了提出算法三种模式的实体对齐率，实体对齐率的定义为：已融合样本与目标实体（第一个数据集实体）的时间相关度差值小于一定阈值的样本所占比值。实验结果可以看出，相比常规的无监督学习，提出算法的概念漂移检测及无监督反向验证过程均在一定程度上提高了实体对齐能力。

以上实验使用了公开数据集的同构数据。随后，为证实提出方法在异构数据集的应用可行性，使用国网安徽省电力公司的实际业务数据进行了实验分析。该数据库包括营销业务应用系统、生产管理系统以及地理信息系统。实验中，将该三类数据库拆分为9个数据集，并通过在同类数据集间设置较高的数据相关度δ（式（10）），构建了多维异构数据环境。本实验选择了基于极大似然估计与K近邻算法(K=10)的实体对齐方法进行了比对分析。

实验方式如下：首先，根据预定义的语料库，对所有异构数据库进行本体关联，定义实体对齐指标。例如，异构数据中实体为“电缆”“缆线”，关系为“故障”“停役”等本体属于互映射本体，其属性为实体及关系所对应的事件（如：发生***区域大规模停电、安排***维修员进行现场抢修等）。之后，在一个数据库中随机提取一个本体，进行实体对齐、实体消歧义及属性融合。最终，根据实体对齐指标，计算已融合本体的TP（True Positive）、FP（False Positive）及FN（False Negative）指标，通过计算准确率（Precision）与召回率（Recall），比较分析F1分数，如式（13）～（15）所示：

图9为F1分数的实验结果比较。本文提出算法的两种模式均得出了较高分数。实验中，K近邻算法根据输入属性，在全局数据库间进行本体的聚类，选择数据库间离聚类中心最为接近的本体。这种方式在低维数据中可得出较好的融合效果，但在高纬度异构数据中，因持续累积的匹配误差，最终得出较差的F1分数。极大似然估计法采用了比较所有实体→属性→关系似然值的全局搜索方式，得出了近似提出算法（无反向验证）的F1分值，但其全局搜索方式需要较高的时间复杂度。

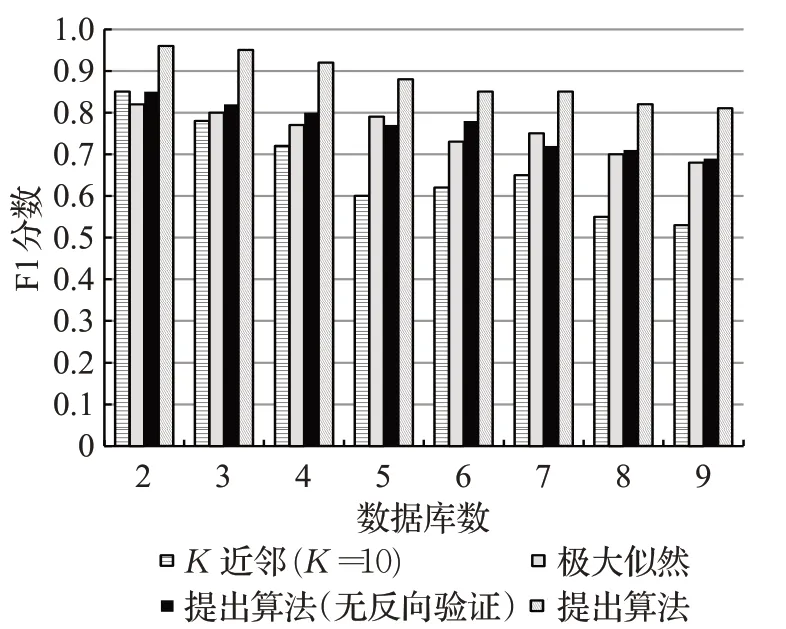
图9 F1分数的比较Fig.9 Comparison of F1 scores

K近邻与极大似然估计法均属于无监督学习算法，在多维数据库中具有较高的时间复杂度。图10中，该类算法的运行时间按数据的维度指数级增长，因而较难应用于高纬度数据集。提出算法的运行时间是线性增长，其中，反向验证过程占用了约20%的算法运行时间。实验中，概念漂移检测的进程与本体融合相互独立，因而未纳入运行时间的比较。

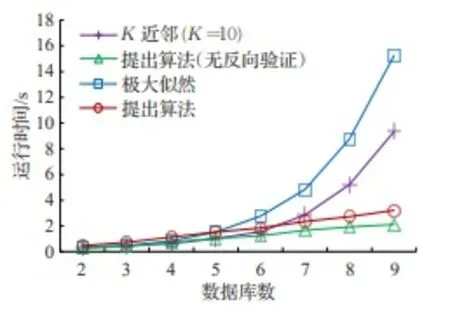
图10 算法运行时间的比较Fig.10 Comparison of run time

总之，提出算法在F1分数和运行时间上均得出了较好的数值。相比K近邻算法，得出了显著提高的F1分数；极大似然估计法与提出算法（无反向验证）得出了类似的F1分数，但提出算法具有较低的时间复杂度，因此体现了良好的算法收敛时间。上述实验证明了提出算法在多维、异构大数据环境的知识融合可行性。

6 结束语

本文面向大数据环境的复杂信息融合应用，提出了一种结合监督学习、概念漂移检测及无监督反向验证的知识融合方法。该方法通过在监督学习中引入周期性概念漂移检测，提高数据模型的可靠性及实体对其效率，并在异构数据集间利用无监督式反向验证算法，有效、高速地进行实体消歧义。目前，提出算法在国网安徽省电力公司知识图谱系统中进行着试点应用，未来工作为选择、比较及优化符合监督学习-概念漂移检测-无监督反向验证的先进算法，进一步提升知识图谱系统在异构大数据环境的应用可行性。