基于动量分数阶梯度的卷积神经网络优化方法

郭明霄，王宏伟，2，王 佳，李昊哲，杨仕旗

1.新疆大学 电气工程学院，乌鲁木齐 830047

2.大连理工大学 控制科学与工程学院，辽宁 大连 116024

3.大连医科大学 基础医学院，辽宁 大连 116041

随着人工智能科技的进步，作为人工智能的重要分支，深度学习越来越多地应用在各行各业中，为人们的社会生产和生活提供了诸多便利。卷积神经网络作为深度学习的核心组成之一，其早期的研究进展较为缓慢，1998年LeCun等人[1]提出了LeNet-5卷积神经网络，并将梯度下降算法应用到卷积神经网络的训练中，这奠定了使用梯度下降算法训练卷积神经网络的基础。进入2010年以来，随着计算机算力的提升，卷积神经网络进入飞速发展时期，相继出现了多种类型的卷积神经网 络 模 型，主 要 有AlexNet[2]、VGGNet[3]、ResNet[4]、GoogLeNet[5]、FCN[6]、DenseNet[7]等。卷积神经网络的应用范围越来越广，尤其在图片分类和分割等方面取得的效果越来越好，但与此同时，网络规模越来越大，复杂程度越来越高，这使得卷积神经网络的训练面临更加复杂的挑战。

法国科学家Cauchy于1874年提出梯度下降法，该算法常用于求解无约束最优化问题，由于算法以目标函数的负梯度方向作为寻找最小值的下降方向，故称为梯度下降法[8]。梯度下降算法常用来训练卷积神经网络，目前，有很多学者以梯度下降算法为基础提出了多种改进型梯度下降算法。常用的改进型梯度下降算法主要有动量梯度下降法[9]，该算法在一定程度上减缓了寻找极值过程中的震荡幅度，加快了收敛速度。文献[10]提出一种动态调整学习率的梯度下降算法，使用该算法训练卷积神经网络，由于学习率减小较快，导致训练后期梯度更新趋向于零，因此会使训练过程提前结束。文献[11]在文献[10]所提算法的基础上进行改进，为减缓学习率衰减速度，新算法使用前几步梯度平方的指数加权平均来进行学习率调整。文献[12]所提算法通过计算梯度的一阶矩估计、二阶矩估计并引入衰减系数来动态改变学习率和梯度下降方向，这使得该算法效率更高，收敛更快。

近几年来，对分数阶微积分的研究引起了诸多学者的兴趣，而分数阶微积分已成功应用到多个领域，如系统辨识[13]、图像处理[14-15]、建模[16]、控制[17-18]等。作为整数阶微积分的推广，分数阶微积分的阶次可为分数，因而分数阶微积分为梯度下降算法开辟了新的研究方向。文献[19]讨论了使用分数阶微分梯度下降算法求解函数最小值时不能收敛到真实最小值的问题，而后提出了可收敛到真实最小值的改进算法，这对使用分数阶微分梯度下降算法解决求取函数最小值问题提供了较强的指导意义。文献[20]指出，将传统梯度下降算法中的整数阶梯度改为分数阶梯度并不能保证算法收敛到真实极小值，并提出了一种更为简洁的、便于实际应用的、可以收敛到真实极值的分数阶梯度下降算法。文献[21]提出了一种新的改进分数阶LMS算法（MFOLMS），该算法克服了准确度和速度二者间的矛盾，既提高了参数估计的准确度又加快了收敛速度。文献[22]采用分数阶微分梯度下降算法对神经网络进行训练，文章分析了训练过程的收敛性，但文中使用的神经网络模型为BP神经网络并非卷积神经网络，后者在处理复杂识别分类任务时使用更为广泛。文献[23]首次将卷积神经网络与分数阶微分梯度下降算法相结合，证实了分数阶微分梯度下降算法在卷积神经网络训练中的可行性，但文章在训练卷积神经网络时仅使用了一个简单的数据集，没有在多个不同复杂程度的数据集上进行进一步的验证，同时文章并没有将分数阶微分梯度下降算法与整数阶梯度下降算法在同一数据集上的效果进行对比。

为了进一步验证分数阶梯度下降算法在卷积神经网络中的可行性，本文将传统梯度下降算法中的动量思想与分数阶梯度下降算法相结合，提出动量分数阶梯度下降算法。实验结果表明，该算法既保证了卷积神经网络的分类准确度，同时又极大减少了数据迭代次数和训练时间。

1 基础知识

在分数阶微积分学领域内广泛使用的分数阶微分定义有三个，分别为：RL（Riemann-Liouville）分数阶微分、GL（Grünwald-Letnikov）分数阶微分、Caputo分数阶微分，其数学表达式分别如下所示。

对于在区间[t0,t]上绝对可积函数f(t)的RL分数阶微分定义为：

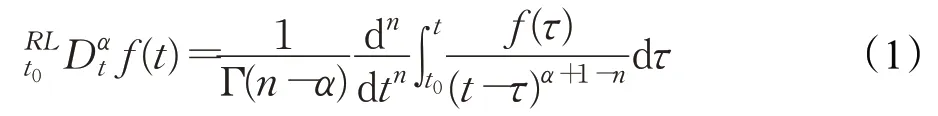
式中，α为分数阶阶次且n-1≤α＜n，n=[α]为不小于α的最小整数，Γ(·)为欧拉Gamma函数，其定义为：

当x为非负整数时可得：

对于在区间[t0,t]上n阶连续可导函数f(t)的GL分数阶微分定义为：

对于在区间[t0,t]上n阶连续可导函数f(t)，若f(n)(t)在区间[t0,t]上绝对可积，则函数f(t)的Caputo分数阶微分定义为：

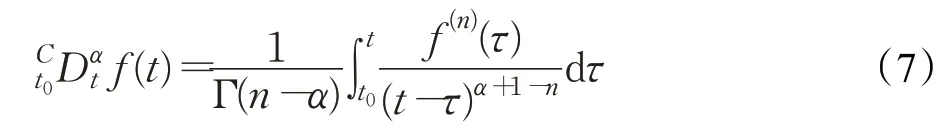
式中，α为分数阶阶次且n-1≤α＜n,n=[α]为整数。

RL分数阶微分和GL分数阶微分在实际使用中要已知信号和信号分数阶导数在初始时刻的取值，而Caputo分数阶微分则需已知信号和其整数阶导数在初始时刻的取值，因而Caputo分数阶微分在实际应用中使用更为广泛[24]。

为方便实际应用，对Caputo分数阶微分方程做无数次分部积分运算的求和形式为：

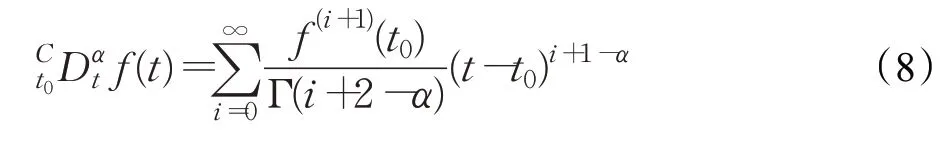
2 问题描述

在实际研究应用中，卷积神经网络常被用来完成图片分类任务，定义卷积神经网络均方误差损失函数如下：

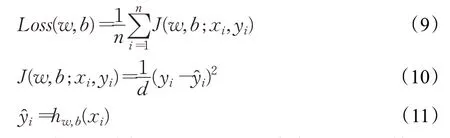
式中，n表示训练集中每一个batch含有的图片个数，xi表示输入到卷积神经网络中的第i张图片，yi代表第i张输入图片所对应的类别标签，y^i则是卷积神经网络计算后输出的第i张图片的类别标签，d为类别标签采用one-hot编码时的编码深度，w、b表示卷积神经网络中各层的链接权重值和神经元偏置值。依据链式求导法则求取误差损失函数对应于各个层的权重和偏置之间的梯度，按照给定学习率和参数更新策略对卷积神经网络各层间的权重和偏置进行更新。训练卷积神经网络的目的是为了提高分类准确率，减小损失函数值，但是随着分类任务越来越复杂，分类精度要求越来越高，卷积神经网络的复杂程度也越来越高，其层数也越来越多，训练难度也相应地越来越大，收敛速度越来越慢，这给整数阶梯度下降算法提出了严峻挑战，而分数阶微分梯度下降算法的出现为解决此项挑战提供了一个新的解决途径。

3 算法推导

文献[8]中的随机梯度下降算法使用负梯度方向对权重和偏置进行迭代更新，简称为SGD算法，结合问本文题描述，将该算法应用于卷积神经网络，则得卷积神经网络梯度更新数学表达式为：

一般，随机梯度下降算法使用整数阶梯度进行参数更新，为使用分数阶梯度下降算法，须先求取分数阶梯度，依据文献[20]给出的关于函数的分数阶梯度求取方法，同时结合本文问题描述，由式（8）可得分数阶梯度下降算法参数更新公式为：

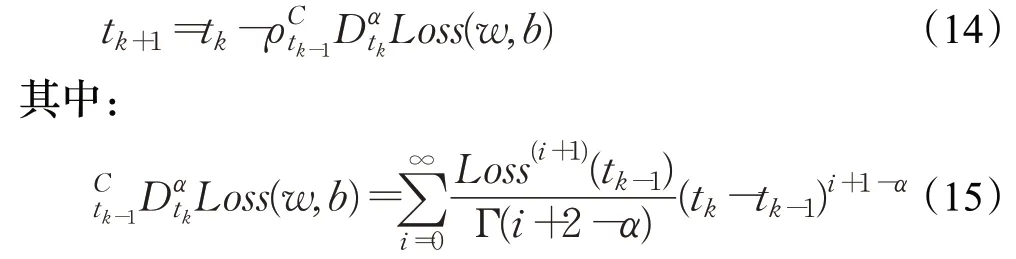
由式（15）可知，分数阶梯度为无穷数列相加，这导致该分数阶梯度算法无法实际应用，为解决此项矛盾，对其展开并取展开式的主要作用项，得分数阶梯度参数更新数学表达式为：

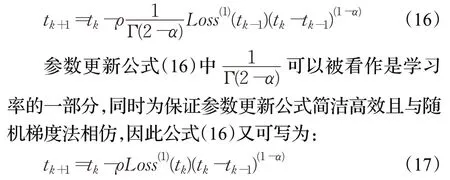
为了在寻优过程中始终保持正向梯度下降方向，同时避免参数更新公式出现奇异值，式（17）又可化为：

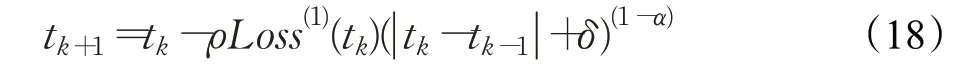
式中，δ值为极小的正数。

至此得出分数阶梯度更新公式，即FOGM算法。将式（18）应用于卷积神经网络，则基于分数阶梯度的卷积神经网络参数更新数学表达式为：

为提高分数阶梯度下降算法性能，可将动量思想与分数阶梯度下降算法相结合，为此需要构建新的梯度下降方向，新的梯度下降方向由动量项和当前分数阶梯度下降方向组成，其中动量项包含了过去时刻的分数阶梯度方向，由式（19）、（20）可得卷积神经网络的权重分数阶梯度和偏置分数阶梯度，则结合动量思想后，卷积神经网络参数更新使用的梯度下降方向为：

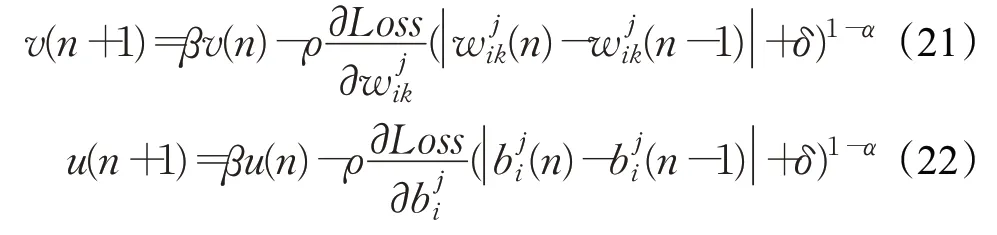
v,u分别表示权重动量项和偏置动量项，β为动量项系数且0＜β＜1,β值决定了过去时刻的梯度更新方向对当前时刻参数更新方向的影响程度。

式（21）、（22）为新的分数阶梯度下降方向构建方法，该方法包含当前时刻的分数阶梯度信息和动量项，即过去时刻的梯度信息，因此，将该方法应用于所求参数更新公式，可得动量分数阶梯度下降算法，简称为MFOGM算法。将过去时刻的梯度和当前时刻的梯度都用于实现系统寻优过程中的参数更新，这有助于减小寻优过程震荡幅度，加快收敛速度，基于动量分数阶梯度下降算法的卷积神经网络参数更新数学公式描述如下：

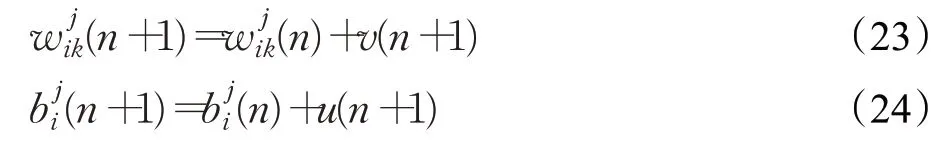
v(n+1)和u(n+1)包含了过去时刻的分数阶梯度信息和当前时刻的分数阶梯度信息，其详细计算过程分别见公式（21）、（22）。

分数阶梯度下降算法的阶次可为分数，参数设置灵活，收敛速度较快，动量项可以减缓寻优过程中的震荡，提高算法收敛速度，动量分数阶梯度下降算法结合这两项优势，既可以保证准确性又可以提高收敛速度。

4 算法测试

为了验证所提MFOGM算法性能，考虑测试函数f(x,y)=x2+y2+1。该函数最小值为f(0,0)=1，初始化坐标(x0,y0)=(0,0)，(x1,y1)=(5.0,-3.0)，动量项v(0)=0，学习率ρ=0.01。

在测试中，令β=0.9,α=(0.4,0.6,…,1.6)，观察不同分数阶阶次对算法收敛性的影响，测试结果见图1。令α=1.2,β=(0.1,0.2,…,0.9)，观察不同动量项系数对算法收敛性的影响，测试结果见图2。

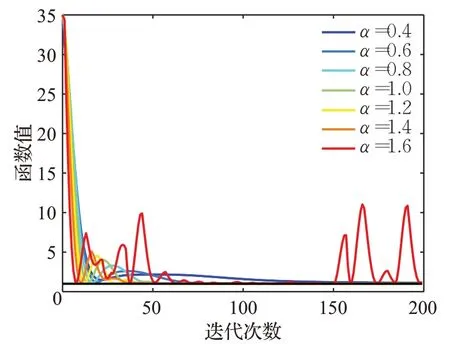
图1 不同分数阶阶次下的收敛情况Fig.1 Convergenceunderdifferentfractionalorders

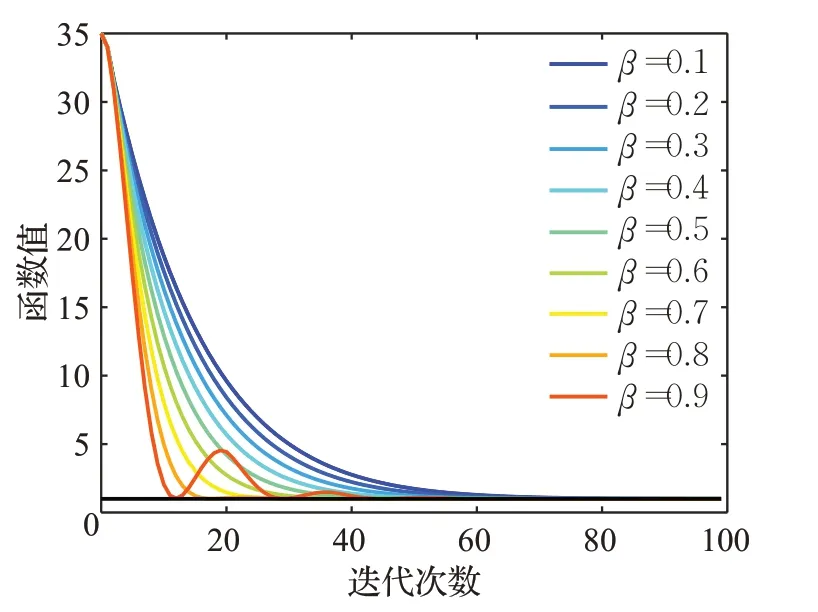
图2 不同动量项系数下的收敛情况Fig.2 Convergenceunderdifferentmomentumcoefficients

由图1可知，当MFOGM算法中学习率ρ和动量项系数β固定不变时，分数阶阶次α取值在一定的范围内由小到大变化，函数f(x,y)收敛到真实最小值的速度由慢到快，若分数阶阶次α取值过大，则会导致函数f(x,y)的值在下降过程中出现较大的震荡甚至无法收敛到真实最小值，因此使用MFOGM算法时应注意分数阶阶次α的取值。

由图2可知，当MFOGM算法中学习率ρ和分数阶阶次α固定不变时，随着动量项系数β值的增大，函数f(x,y)收敛于真实最小值的速度也随之加快，当动量项系数取值过大时会使收敛曲线产生震荡，但依然会使函数f(x,y)收敛于真实最小值。较大的动量项系数有助于在梯度下降过程中逃脱局部最小值陷阱，因此采用MFOGM算法在高维复杂空间寻找最小值时建议使用较大的动量项系数。

综上所述，在一定的取值范围内，函数值曲线随着分数阶阶次α的增加收敛速度不断加快，随着动量项系数β的增加收敛速度不断加快，动量项系数和分数阶阶次二者分别与收敛速度成正相关性。因此，使用MFOGM算法在函数寻找最小值时，通过设置适当的参数值可以保证寻找到真实最小值，从而达到收敛效果。

5 实验设计

5.1 开发环境介绍

本实验所用操作系统：Win10家庭中文版，处理器：英特尔酷睿I5-8265U，显卡：英伟达MX250，Python版本：Python3.7.764bit，开发环境：tensorflow2.1.0。

5.2 卷积神经网络结构描述

在实验中，使用改进后的LeNet-5卷积神经网络，网络模型见图3，该网络输入图片大小为32×32像素，共包含两个卷积模块和一个全连接模块。第一个卷积模块包含有卷积层、BatchNormalization、ReLU激活函数、MaxPool层，输入图片经过第一个卷积模块后生成6个分辨率为14×14的featuremap。第二个卷积模块同样包含有卷积层、BatchNormalization、ReLU激活函数、MaxPool层，第一个卷积模块输出的featuremap经过第二个卷积模块后生成16个分辨率为5×5的featuremap。网络的第三个模块为全连接模块，该模块由两个全连接层、一个输出层、两个ReLU激活函数构成，每层神经元的个数依次为120，84，10，该模块的输入来自第二个卷积模块的输出，最后的输出层没有使用ReLU激活函数而是直接输出。

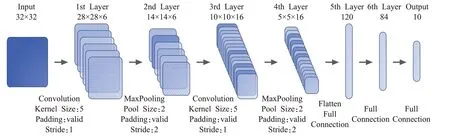
图3 卷积神经网络模型Fig.3 Convolutional neural network model

5.3 实验设计

为了验证MFOGM算法的性能，使用随机梯度下降算法（SGD）、动量随机梯度下降算法（MSGD）、动量分数阶梯度下降算法（MFOGM）在三个数据集上进行图片分类性能比较。这三个数据集分别是Mnist数据集、FashionMnist数据集、Cifar10数据集，数据集的复杂程度逐渐增加。训练时将数据集划分为训练集和验证集，在训练集上对卷积神经网络进行训练，同时记录训练误差损失值，在验证集上验证并记录卷积神经网络的分类准确率。另外，由于Mnist数据集和FashionMnist数据集中图片大小为28×28像素，因此使用这两个数据集进行训练时，需要将LeNet-5卷积神经网络中，第一个卷积层的Padding设置为same，其他一些关于算法参数的初始化见表1。

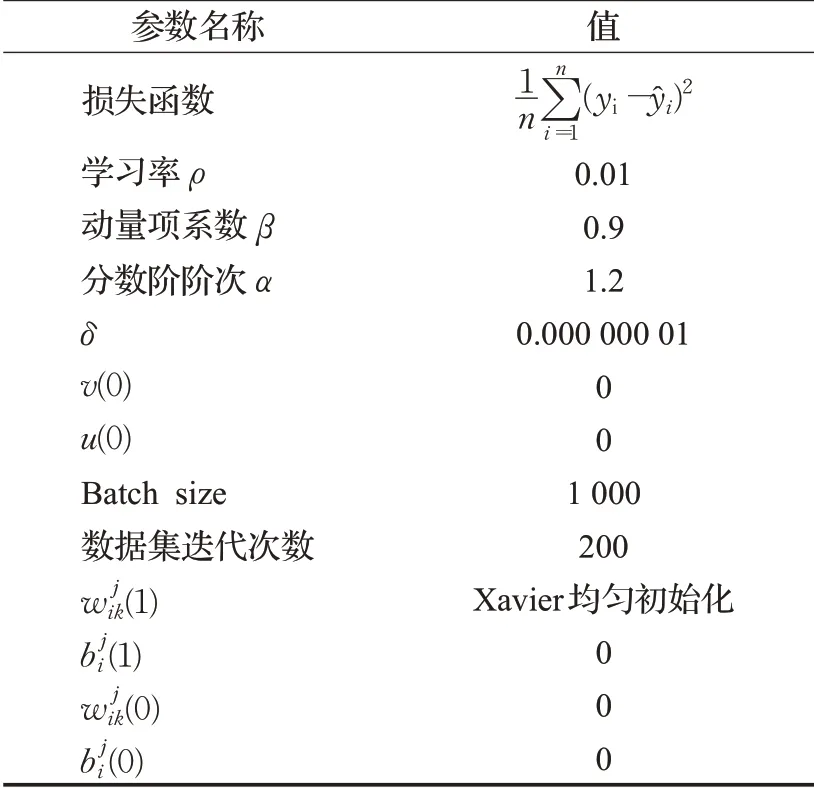
表1 参数初始化Table 1 Parameter initialization

Mnist数据集集合了0～9这10类手写数字黑白图片，共有70 000张，大小为28×28像素，其中60 000张用作训练集，10 000张用作验证集。FashionMnist数据集集合了10种人类服装的黑白图片，分别为T恤、裤子、套头衫、连衣裙、外套、凉鞋、衬衫、运动鞋、包、靴子，共有70 000张，大小为28×28像素，其中60 000张用作训练集，10 000张用作验证集。Cifar10数据集集合了10种物体的彩色图片，分别是飞机、汽车、小鸟、猫、鹿、狗、蛙、马、船、卡车，共有60 000张，大小为32×32像素，其中50 000张用作训练集，10 000张用作验证集，三个数据集中的部分图片见图4。

图4 不同数据集展示Fig.4 Display of different datasets

5.4 实验结果分析

由图5可得，在Mnist数据集上进行200次迭代训练后，MFOGM算法能够以最少的迭代次数使卷积神经网络达到收敛，且准确率较高。MSGD算法在训练初期使准确率上升较快，后期上升较为平缓，在经过200次迭代训练后未达到收敛，在快速性上落后于MFOGM算法。SGD算法的快速性与MSGD算法、MFOGM算法都有着一定的差距，未达到收敛。从图6可以看到，经过相同的训练次数后，采用MFOGM算法取得的训练误差最小，其次为MSGD算法，采用SGD算法得到的误差与前两者相比有一定的差距。由此可知，在Mnist数据集上经过相同的训练迭代次数后，使用MFOGM算法训练后的卷积神经网络性能优于使用SGD算法或MSGD算法训练后的卷积神经网络。

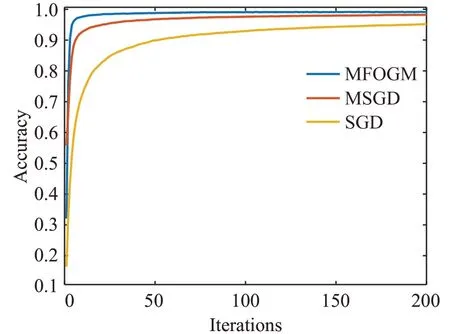
图5 三种算法在Mnist数据集上准确度对比曲线Fig.5 Accuracy comparison curves on Mnist dataset

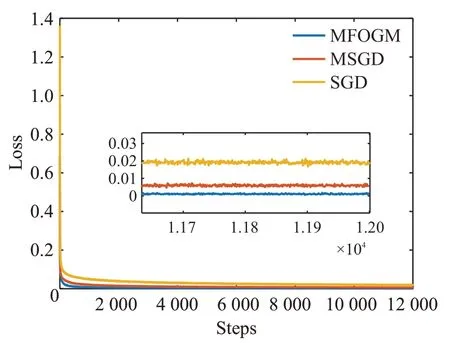
图6 三种算法在Mnist数据集上训练损失对比曲线Fig.6 Training loss comparison curves on Mnist dataset

由图7可知，在FashionMnist数据集上进行200次迭代训练后，三种梯度下降算法在验证集分类准确率上有明显区别。MFOGM算法以最快的速度使卷积神经网络达到收敛，且准确率较高。采用MSGD算法得到的准确率曲线呈现出平缓上升过程，未达到收敛。采用SGD算法得到准确率曲线与前两者有明显差距，未达到收敛。从图8可以看出，经过相同的训练迭代次数后，采用MFOGM算法得到的训练误差最小，MSGD算法次小，SGD算法的训练误差最大。因此，在FashionMnist数据集上经过相同的训练迭代次数后，采用MFOGM算法的卷积神经网络取得的整体性能最优。

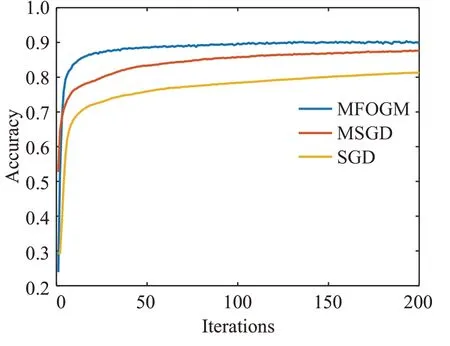
图7 三种算法在FashionMnist数据集上准确度对比曲线Fig.7 Accuracy comparison curves on FashionMnist dataset

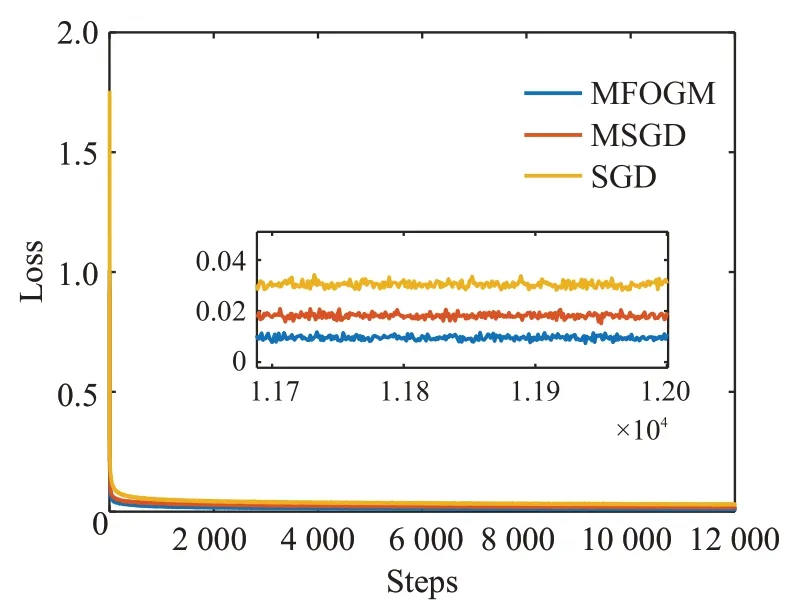
图8 三种算法在FashionMnist数据集上训练损失对比曲线Fig.8 Training loss comparison curves on FashionMnist dataset

图9显示出，在Cifar10数据集上进行200次的迭代训练后，采用三种算法得到的验证集分类准确率曲线图有了显著区别。MFOGM算法依然以最快的速度使卷积神经网络达到收敛，准确率较高，优势显著。采用MSGD算法得到的准确率曲线呈现明显上升过程，未达到收敛。SGD算法在验证集分类准确率上的效果远不如MSGD算法和MFOGM算法，未达到收敛。从图10可以看出，经过相同的迭代训练次数后，采用MFOGM算法取得的训练误差最小，采用MSGD算法得到的训练误差次小，采用SGD算法在训练损失误差中取得的误差值最大。由此可知，在Cifar10数据集上经过相同的训练次数后，采用MFOGM算法的卷积神经网络取得的整体性能最优。

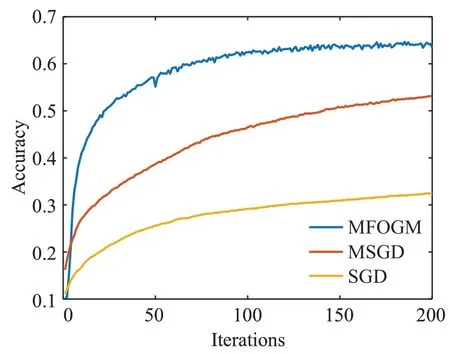
图9 三种算法在Cifar10数据集上准确度对比曲线Fig.9 Accuracy comparison curves on Cifar10 dataset

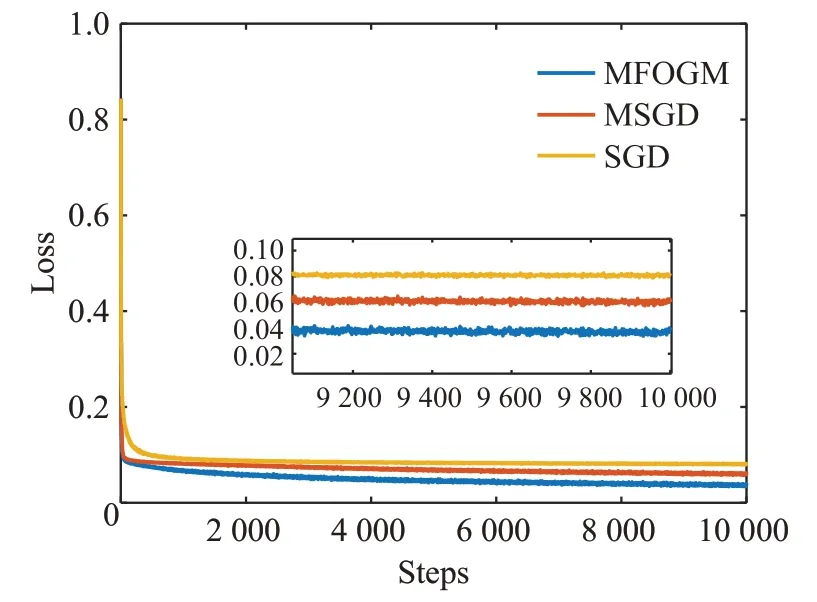
图10 三种算法在Cifar10数据集上损失对比曲线Fig.10 Training loss comparison curves on Cifar10 dataset

综上所述，通过在三种不同复杂程度的数据集上采用相同的卷积神经网络和训练迭代次数，对MFOGM、MSGD、SGD三种算法进行对比，依据得到的验证集准确度曲线图和训练误差损失曲线图可知，MFOGM算法可以使卷积神经网络快速达到收敛，且准确率较高，收敛速度优于MSGD算法和SGD算法，并且数据集越复杂，采用MFOGM算法的优势越明显。

在实际应用中，使卷积神经网络达到收敛时所花费的时间是验证算法性能的重要指标。表2、表3、表4给出了三种算法在三种数据集上取得的分类准确度、所需迭代次数和时间消耗，其中，准确度是指在验证集上的准确度。

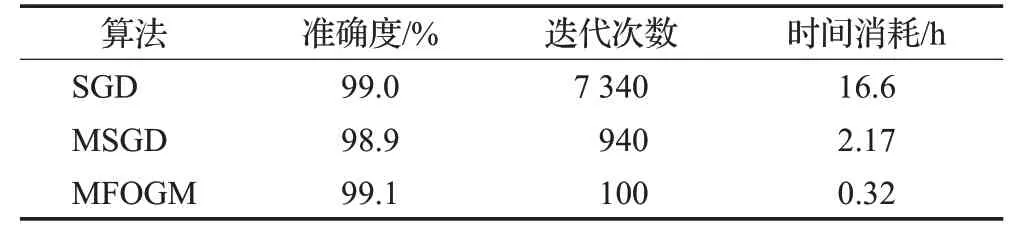
表2 三种算法在Mnist数据集上时间消耗Table 2 Time consumption of three algorithms on Mnist dataset

表3 三种算法在FashionMnist数据集上时间消耗Table 3 Time consumption of three algorithms on FashionMnist dataset

表4 三种算法在Cifar10数据集上时间消耗Table 4 Time consumption of three algorithms on Cifar10 dataset

由表2、表3、表4可知，在使用同一卷积神经网络的情况下，三个算法在同一数据集上取得的准确度无明显差别。在Mnist数据集上，MFOGM算法使卷积神经网络达到收敛所需时间比MSGD算法大约少了85.25%，比SGD算法大约少了98.07%，在FashionMnist数据集上，使用MFOGM算法达到收敛所需时间比MSGD算法大约少了76.98%，比SGD算法大约少了97.65%，在Cifar10数据集上，使用MFOGM算法达到收敛所需时间比MSGD算法大约少了78.42%，比SGD算法大约少了97.53%。总之，MFOGM算法可以以较高的准确度、较少的迭代次数、极少的训练时间完成卷积神经网络的训练，为训练卷积神经网络节省大量时间成本。

6 结束语

卷积神经网络应用越来越广泛，性能越来越强，规模越来越大，层次越来越深，训练难度也越来越大。分数阶作为近几年的研究热点，已经用到多个领域并取得了较好的实际应用效果，但将分数阶梯度应用到卷积神经网络的相关文章较少，为此，本文提出了动量分数阶梯度下降算法。首先，通过测试函数验证了所提算法的性能，并分析了不同分数阶阶次和动量项系数对算法性能的影响；接着，将动量分数阶梯度下降算法应用到卷积神经网络的训练过程中，完成卷积神经网络的训练，实验结果表明，该算法可以使卷积神经以较高的分类准确率达到收敛，同时，相对比传统的梯度下降算法和动量梯度下降算法，该算法可以极大地提高卷积神经网络的收敛速度，这为训练卷积神经网络节省了大量的时间成本，具有较强的实际应用意义。在本文中，分数阶阶次的取值为固定值，若将分数阶阶次设置为动态自适应调节，这对卷积神经网络训练的影响是下一步值得探讨的研究方向。