改进人工势场法的移动机器人避障轨迹研究

李二超，王玉华

兰州理工大学 电气工程与信息工程学院，兰州 730050

随着人工智能的快速发展，移动机器人被广泛应用于工业、军事以及医学等领域。而路径规划算法被广泛地应用在移动机器人的导航中，机器人如何从所处的环境中搜索一条从初始位置到终点的安全、无碰撞的最优路径是路径规划的关键[1]。常用的算法有A*算法、蚁群算法（ant colony optimization，ACO）、Dijkstra算法、遗传算法（genetic algorithm，GA）、快速随机搜索树法（rapidlyexploring random tree，RRT）、粒子群算法（particle swarm optimization，PSO）和人工势场法（artificial potential field，APF）等[2]。其中，A*算法引入了启发函数避免了路径规划问题中产生大量的无效搜索路径；ACO是一种启发式随机搜索算法，存在计算量大、收敛速度慢等问题[3]；Dijkstra算法主要特点是由中心向外扩散，直到扩展到终点为止，但其遍历计算节点较多，效率较低[4]GA得到的路径符合现实中路径选择需求，但运算量大且耗时长，无法满足实时性的需求[5]；RRT是一种基于采样的概率算法，其特点主要是在空间中随机生成新节点并在新节点上继续向目标点延伸，但存在路径不平滑，搜索路径一直变化的情况[6]；PSO同GA都是迭代算法，相较于GA，PSO收敛速度较快，但粒子同一化后，收敛速度较慢，且收敛精度不够。

人工势场法在路径规划中只需要根据当前机器人的位姿以及障碍物来确定下一步的运动，算法本身具有计算量小、反应速度快、生成路径平滑等优点被广泛用于运动规划系统的移动机器人中。Rostami等[7]在传统人工势场函数中加入调节因子来绕过障碍物从而克服局部最小值和目标不可达问题；Yao等[8]从强化学习的视角来解决复杂环境问题，将黑洞人工势场和强化学习结合来解决局部稳定点问题，但在路径规划过程中会出现振荡现象；赵明等[9]提出域来解决多目标点任务的局部稳定点问题，在机器人陷入局部极小值时通过域场逃离局部极小点，但未考虑多复杂环境下机器人能否到达目标点；何乃峰等[10]基于模拟退火算法，重新构建斥力势场函数模型，从而设计逃离局部极小值控制器进行全局路径，全局路径平滑，但所规划路径并不是最优路径；徐小强等[11]针对陷阱区域和局部极小值问题，提出提前预测人工势场法，但对于较多障碍物的复杂环境而言，仍不能完整规划路径；王迪等[12]提出基于虚拟目标点和环境判断的改进方法，实现移动机器人的局部路径规划，但在遇到陷入型障碍物时规划出“沿壁走”的路径存在消耗程距的问题；曹凯等[13]设计了一种由人工势场引导RRT*进行路径规划的方法来解决障碍物密集、通道狭窄的环境，但面对陷入型环境问题时，偏向区域搜索会导致可行区域的收敛性，使路径规划采样点不完整，无法完成路径的完整性；高志伟等[14]提出将轨迹跟踪和机器人动力学控制模型相结合，实现全局路径规划点作为局部目标点来得到能耗最优轨迹，但这种规划方式面对更复杂环境时全局路径规划点和局部路径规划点的判断无疑加大了计算时间和耗能。

针对上述算法的不足，本文提出了一种简化障碍物预测碰撞人工势场法（simplified obstacles and predict collision of artificial potential field method，SOPC-APF）。首先，加入预测碰撞思想，帮助机器人在未知环境中通过传感器探测进行提前预判，避免机器人陷入局部最优；其次简化机器人受障碍物影响范围内的障碍物——即只考虑目标点一侧障碍物斥力的影响；最后通过虚拟目标点的加入，采用改进斥力因子影响范围的斥力函数引导机器人快速、平稳、无碰撞地到达目标点。最后在仿真平台对SOPC-APF进行可行性的验证。

1 APF算法基本原理

人工势场法作为路径规划算法中广泛应用的一种算法，最早由Khatib[15]所提出。在人工势场算法中，将机器人的运动环境看作为一个虚拟力场，目标点和障碍物在机器人运动过程中产生引力和斥力，通过两者的合力作为机器人运动的加速度来控制机器人向目标点移动。

假设移动机器人在二维有限空间内运动受力分析如图1所示，且机器人在二维有限空间中的位置表示为q=(x,y)T，目标点位置表示为qtarg=(xT,yT)T，障碍物位置表示为qobs=(xo,yo)T。

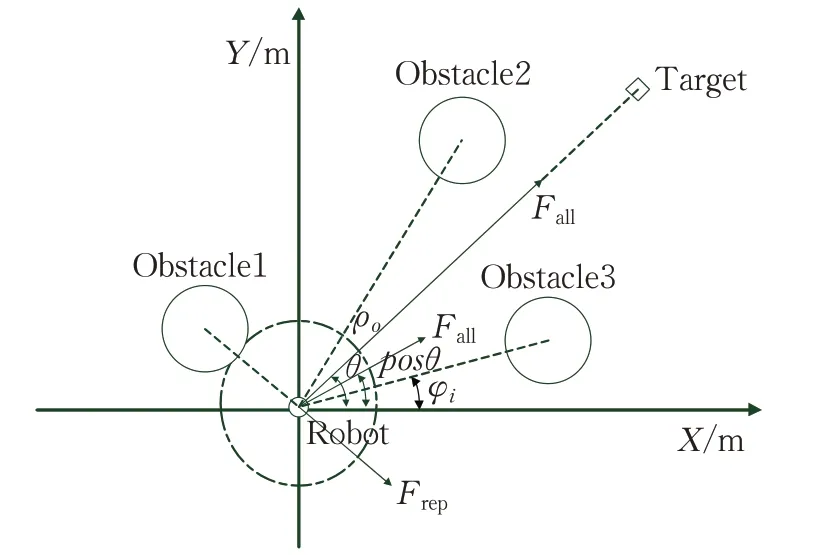
图1 传统人工势场法受力分析Fig.1 Force analysis of traditional APF

目标点对机器人产生的引力场为Uatt(q)，障碍物对机器人产生的斥力场为Urep(q)，即机器人最终所受到的合力场为Utotal(q)，则可表达为：

式中，α为斥力势场增益系数，‖q-qobs‖为机器人与障碍物之间的欧几里德距离，ρo为障碍物斥力场对机器人产生斥力作用的影响距离，若‖q-qobs‖小于该值，受斥力作用，反之不受作用。

引力势场函数的负梯度为机器人所受到的引力为：

当机器人处于各障碍物影响距离内时，机器人所受到的合斥力为，即机器人所受到的合力Ftotal为：

2 SOPC-APF算法

针对APF算法存在的缺陷，本文提出了SOPC-APF算法，该算法能够在未知场景中根据传感器探测出的环境信息，提高APF算法的全局搜索能力，减小某些局部震荡产生的局部路径消耗。SOPC-APF算法首先对机器人前方的障碍物进行预测碰撞处理，从而简化影响范围内的受限障碍物（机器人当前位置与目标点之间存在的障碍物称为受限障碍物）；在简化后的受限障碍物中通过旋转角度来设置最优的虚拟目标点；最后结合虚拟目标点的轨迹找寻真实目标点，从而生成一条路径平滑且连续的最优路径，从而使移动机器人沿着该全局优化路径快速、平稳、安全地到达目标点。SOPC-APF算法的大体流程图示意如图2所示。

图2 SOPC-APF流程图Fig.2 Flow chart of SOPC-APF

针对移动机器人在多障碍物影响范围内时受多个障碍物各个方向的影响出现合力为零或者机器人在某一范围内来回振荡的情况，本文提出一种简化障碍物的思想，即移动机器人只考虑在目标点一侧障碍物的斥力函数影响，如图3所示。在简化过程中，令移动机器人在当前位置Xj处剔除(O1,O5,O6)，若保留障碍物(O1,O5)，其产生的斥力F1,5对逃离(O2,O3,O4)组成的受限障碍物的斥力有较大影响，导致与目标点产生的引力发生不必要的振荡，使后续的路径规划算法效率降低，所有在当前位置Xj处，考虑(O1,O5)是完全没有必要的。

图3 简化障碍物图Fig.3 Map of simplified obstacles

定义1机器人处于n个障碍物影响距离内时，机器人只受m(m∈n)个障碍物斥力作用，则移动机器人所即机器人所受到的合力受到的合斥力为Ftotal为：

2.1 碰撞预测

当移动机器人通过传感器检测出地图存在陷阱区域时，如U型障碍物等复杂障碍物，传统的人工势场法由于算法自身的缺陷会出现震荡或停止的现象，以致于不能完整地规划出路径。因此本节引入了预测距离和虚拟目标点来引导移动机器人绕开陷阱区域，规划完整路径。

2.1.1 预测距离

针对陷阱区域的提前预知，如U型，陷入型障碍物，传统算法会在陷阱区域内发生震荡或者停止，无法规划出完整路径。因此引出预测距离Rp，通过比较移动机器人到简化障碍物之间的距离r0来判断自己的下一步位置，若小于，通过偏转角度来设置虚拟目标点；否则按照初始方向向目标点靠近。对于偏转角度的实现以移动机器人当前位置为圆心，m个障碍物距离机器人最远的障碍物为半径偏转角度γ来绕开m个障碍物。使每次旋转3°直到简化后的障碍物在机器人安全范围之外停止旋转。则偏转角度可表示为：

2.1.2 虚拟目标点

通过偏转角度γ，在m个障碍物中距离机器人最远的障碍物为半径的另一端设置虚拟目标点，在虚拟目标点的引导下，使机器人向虚拟目标点移动，到达虚拟目标点后主动撤销虚拟目标点。重复以上步骤，直到机器人到达目标点。找寻最优虚拟目标点的伪代码如算法1。

算法1设置虚拟目标点算法

2.2 改进斥力函数

在二维有限空间中，改进斥力场函数为：

改进受力分析如图4所示。其中，FR1是m个障碍物对机器人的斥力分量，FR2是目标点对机器人的引力分量。

图4 改进势场函数受力图Fig.4 Force analysis of improved APF

算法2改进斥力场函数算法

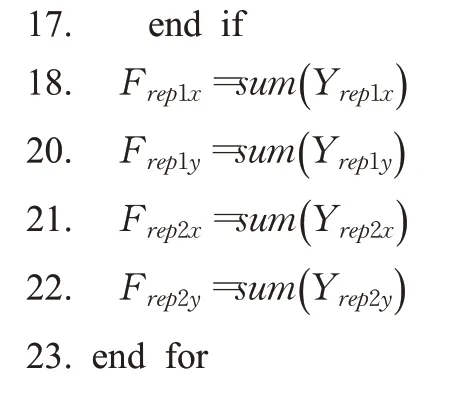
3 算法仿真及结果分析

为验证SOPC-APF算法的可行性和路径规划的效果，在实验平台中进行仿真研究，研究过程中，将移动机器人视为一个质点，分别对传统人工势场法和改进人工势场法在目标不可达、局部极小值点以及复杂环境下地图中做出对比，从而验证出SOPC-APF的优越性。

3.1 基础地图算法对比分析

若将初始参数设置如下：机器人初始位置Xo=( 0,0)，目标点位置Xg=(1 0,10)，引力系数ks=15，斥力1系数α=1.1，斥力2系数M=2，障碍物影响范围ρo=2.5，预测碰撞距离Rp=2，步长L=0.1，障碍物半径R=0.5。图5所示为移动机器人-障碍物-目标点目标点不可达问题。

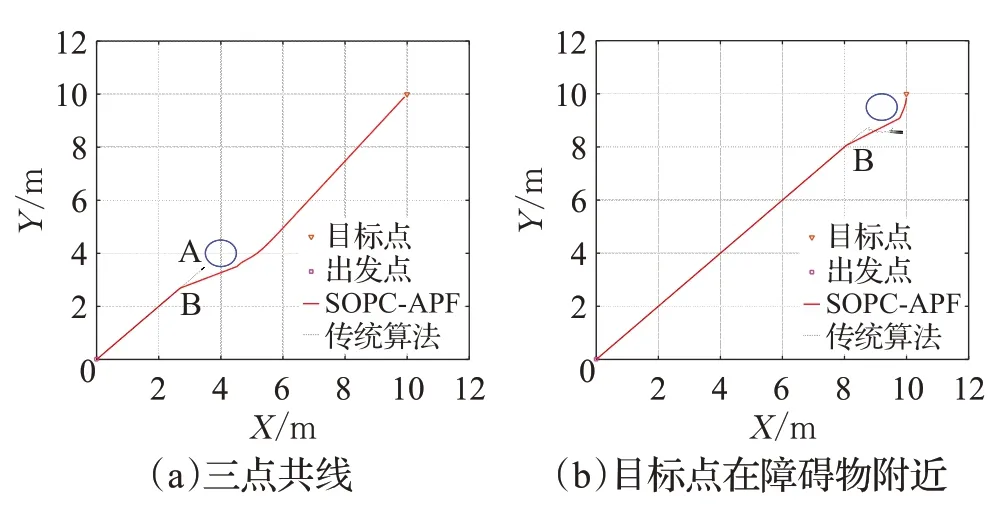
图5 目标不可达问题Fig.5 Problem of unreachable goals

图5（a）为三点共线问题，障碍物处于移动机器人和目标点两点之间的连接线上，传统算法在A点时斥力引力产生的合力在某一范围震荡，导致传统算法无法逃出该范围到达目标点；SOPC-APF在B点碰撞预测后发现障碍物，及时偏转角度脱离合力震荡范围，从而到达目标点。图5（b）中目标点处于障碍物的影响范围内且距离障碍物较近，因此传统算法会受到的斥力比较大，引力较小，会出现在目标点附近抖动现象；SOPC-APF则在B点处对障碍物的预判，从而通过偏转角度设置虚拟目标点，到达虚拟目标点后重新规划到达目标点的路径。

图6 局部极小点问题Fig.6 Problem of local minimum

设置参数如下：机器人初始位置Xo=(5 .5,2.5)；目标点位置Xg=(1 0.5,10.5)。图7为陷入陷阱区域问题，机器人起点被障碍物包围，传统算法在到达A点处受到合斥力影响，在A点处产生振荡，无法逃脱半包围障碍物；SOPC-APF在起点处通过预测距离判断出移动机器人与目标点之间已存在障碍物，则在全局障碍物中找出所有与该障碍物相连的障碍物，即受限障碍物，对受限障碍物及时旋转角度设置虚拟目标点B，从而逃出半包围障碍物，规划处达到目标点路径。

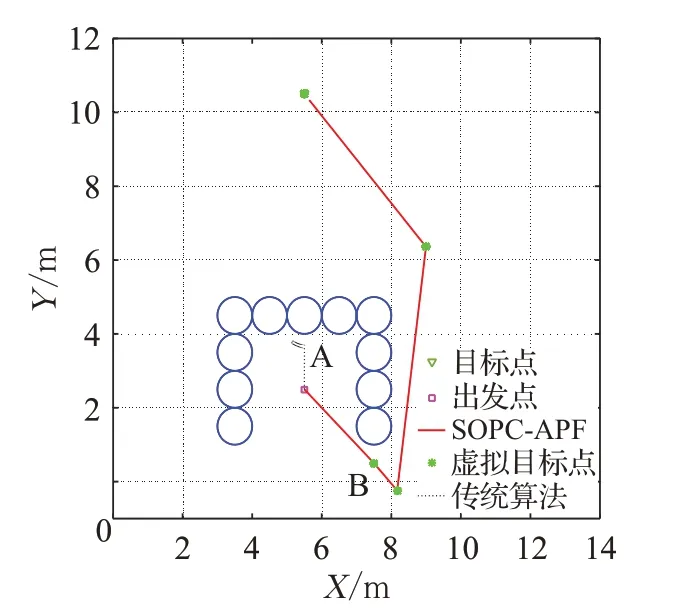
图7 陷入问题Fig.7 Problem of trapping

仿真数据结果如表1所示，验证了SOPC-APF对于目标不可达和局部极小值点问题路径规划的可行性和安全性。

表1 基础地图算法对比数据Table 1 Basic map algorithm compares data

3.2 复杂地图算法对比分析

若将基础参数设置如下：机器人初始位置Xo=( 0.5,0.5)，目标点位置Xg=(1 9.5,19.5)，引力系数ks=15，斥力1系数α=1.1，障碍物影响范围ρo=2.5，预测碰撞距离Rp=4，步长L=0.2。在不同复杂障碍物下对本文算法、传统人工势场法、文献[16]中改进的蚁群算法（记作A-ACO）、文献[7]改进的人工势场法（记作BAPF）、文献[11]改进的人工势场法（记作C-APF）进行多次比较，从而验证本文算法可以克服人工势场在复杂障碍物不适用等问题。传统人工势场法由于自身的缺陷，在复杂环境中会出现振荡现象，无法成功完成路径规划；A-ACO算法属于全局路径规划算法可以很好地避障从而完成路径规划，但相比较人工势场法运行时间较长；B-APF在遇到障碍物时通过绕过受限障碍物来规划路径，这样导致路径过长；C-APF引入预测距离和机器人安全距离，在障碍物受限之前作出反应，通过设置虚拟目标点规划出来的路径较短；SOPC-APF在C-APF基础上对受限障碍物进行简化处理，在斥力函数中加入目标点和机器人的相对距离，通过障碍物影响范围内M取值情况的分类，从而使机器人的规划路径最短且平滑。

3.2.1 随机离散障碍物地图

若障碍物环境是离散分布的，几种算法在同一仿真环境下运行，设置M=0.5，R=0.65。仿真对比结果如图8（a）所示。图8（b）为SOPC-APF的引力和斥力能量图，引力的大小趋于0，表示移动机器人已到达目标点，从图8（b）中可知机器人抵达目标点步数不超过150步，且机器人合力方向较平稳，说明生成路径较光滑。从表2数据对比可以看出，SOPC-APF相较于A-ACO算法速度提高99.05%，转折数量减少了1个；相较于B-APF算法路径缩短了37.78%，算法速度提高了67.95%；相较于C-APF算法转折数量减少了1个。

图8 离散障碍物中SOPC-APF路径规划Fig.8 SOPC-APF path planning in discrete obstacles

3.2.2 L型、离散障碍物地图

若障碍物环境中存在L型障碍物和离散障碍物，几种算法在同一仿真环境下运行，设置M=2，R=0.9。仿真对比结果如图9（a）所示，传统算法未达成功到达目标点。图9（b）为SOPC-APF的引力和斥力能量图。从表3数据对比可以看出，SOPC-APF相较于A-ACO算法路径缩短了5.48%，速度提高了99.05%，转折数量减少了6个；相较于B-APF算法路径缩短了3.50%，算法速度提高了30.0%；相较于C-APF算法路径缩短了2.13%。

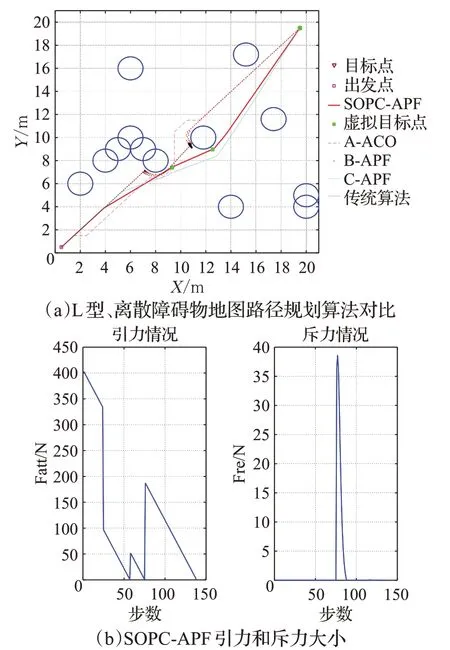
图9 L型、离散障碍物中SOPC-APF路径规划Fig.9 SOPC-APF path planning in L-shaped and discrete obstacles

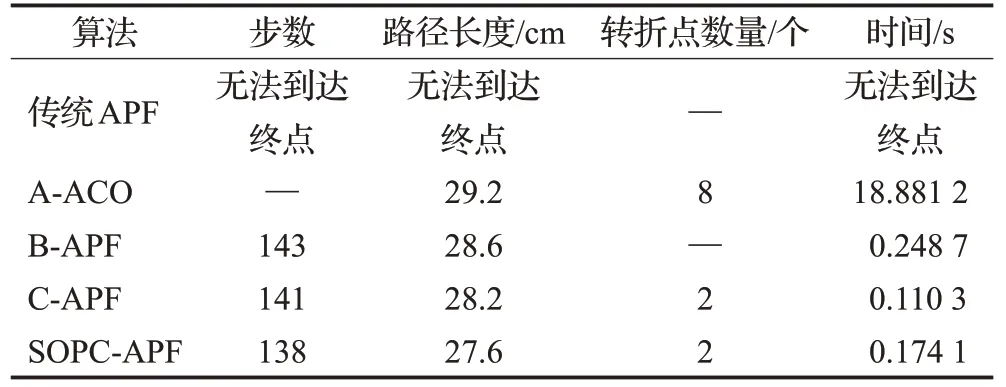
表3 L型、离散障碍物路径规划算法数据对比Table 3 Comparison of path planning algorithms for L-shaped and discrete obstacles

3.2.3 U型、离散障碍物地图

若障碍物环境中存在U型障碍物和离散障碍物，几种算法在同一仿真环境下运行，设置M=1.5，R=1。仿真对比结果如图10（a）所示，（b）为SOPC-APF的引力和斥力能量图。从表4数据对比可以看出，SOPC-APF相较于A-ACO算法路径缩短了2.05%，速度提高了99.06%，转折数量减少了10个；B-APF算法在该地图中由于陷入障碍物太深，无法通过B-APF算法绕出，因此路径规划失败；相较于C-APF算法路径缩短了2.72%。

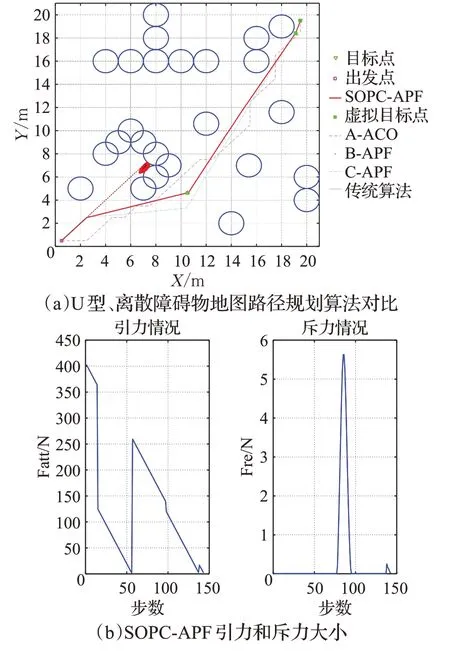
图10 U型、离散障碍物中SOPC-APF路径规划Fig.10 SOPC-APF path planning in U-shaped and discrete obstacles

3.2.4 复杂障碍物地图

（1）若存在密集障碍物等复杂环境下，几种算法在同一仿真环境下运行，设置M=1.5，R=0.5，Rp=6。仿真对比结果如图11（a），图11（b）为SOPC-APF的引力和斥力能量图。

图11 复杂障碍物中SOPC-APF路径规划Fig.11 SOPC-APF path planning in complex obstacles

从表5数据对比可以看出，SOPC-APF相较于AACO算法路径缩短了4.83%，速度提高了99.06%，转折数量减少了7个；B-APF算法路径缩短了56.15%，速度提高了94.61%；C-APF算法由于该地图过于复杂无法完整的规划出路径。

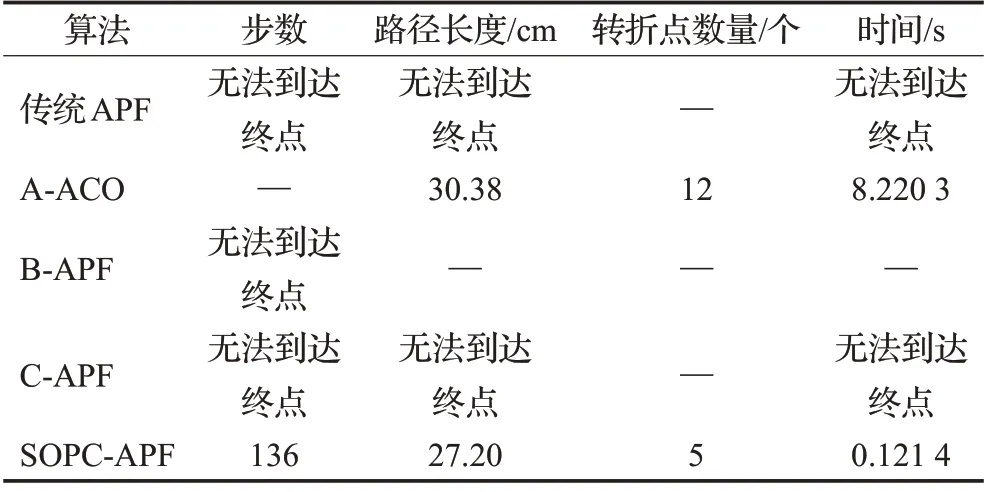
表5 复杂路径规划算法数据对比Table 5 Comparison of complex obstacles path planning algorithm data

（2）若移动机器人起点处于半包围障碍物等复杂环境下，几种算法在同一仿真环境下运行，设置M=1.5，R=0.5，Rp=4。仿真对比结果如图12（a）所示，图12（b）为对应的的引力和斥力能量图。

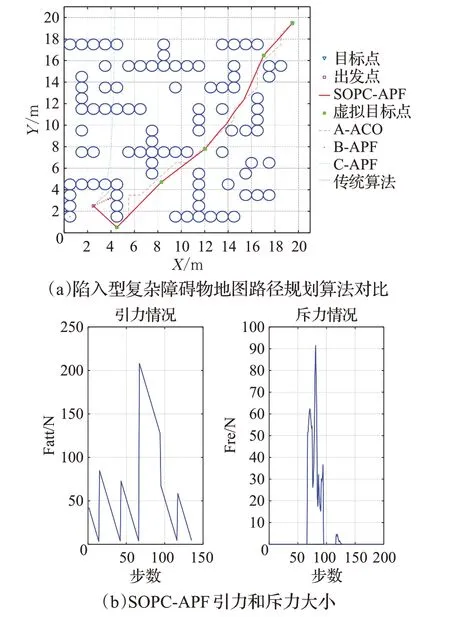
图12 复杂障碍物中SOPC-APF路径规划Fig.12 SOPC-APF path planning in complex obstacles

从表6数据对比可以看出，SOPC-APF相较于AACO算法路径缩短了1.05%，速度提高了98.52%，转折数量减少了8个；B-APF和C-APF算法由于陷入障碍物内部，无法完整地规划出路径。

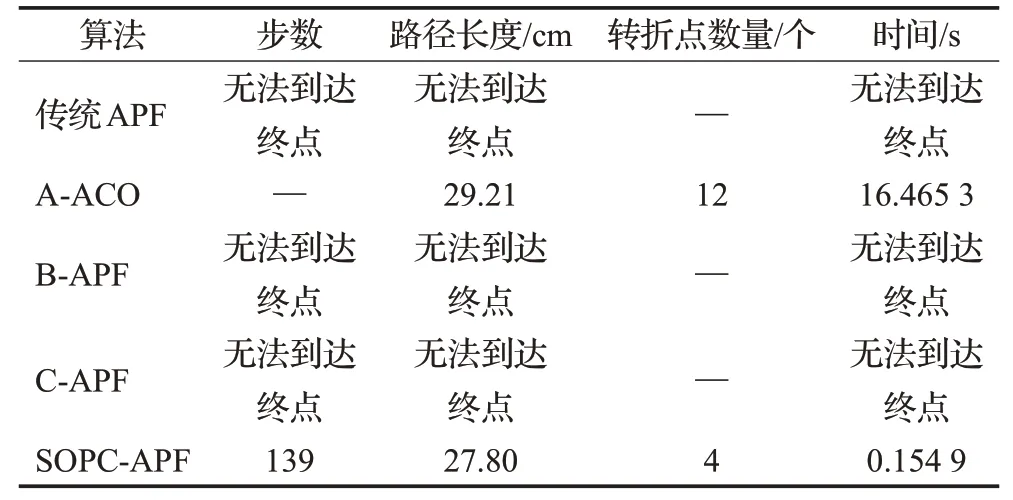
表6 复杂路径规划算法数据对比Table 6 Comparison of complex obstacles pathplanning algorithm data

图13为上述环境下移动机器人的合力方向的对比分析，而移动机器人面对目标点的角度问题也可以看作移动机器人相对路径平稳性的评估，从对比图中不难看出：在相同仿真环境下，传统算法面对目标不可达、局部极小值以及陷入问题时出现的震荡问题，使移动机器人路径波动大，稳定性不理想；SOPC-APF在设定迭代次数内可到达目标点，且运行路径较平滑，无震荡现象出现。

图13 合力方向对比分析Fig13 Comparative analysis of total force direction

通过以上仿真实验结果得到如下结论：当环境复杂，存在陷阱区域、初始位置陷入环境以及密集障碍物时，SOPC算法可以安全地逃离或避开陷阱区域和穿越密集环境，且轨迹平滑；当地图中存在较为简单的目标不可达和局部极小点问题的障碍物环境时SOPC算法也可以规划出相比人工势场法更加简洁的轨迹，且无震荡轨迹发生。

4 结论

针对传统人工势场法目标不可达，易陷入局部最优，且不适用于复杂环境下等问题导致移动机器人无法规划出完整路径，因此本文提出一种改进——基于简化障碍物预测碰撞人工势场法。首先，在机器人移动前对前方路径进行预测判断；在预测到存在障碍物后，简化受限障碍物，即机器人只受影响范围内目标一侧障碍物的斥力影响；随后在简化后的障碍物附近设置合理的虚拟目标点，经改进的斥力函数引导机器人在复杂环境中快速生成一条路径平滑、平稳、无碰撞的路径。

仿真实验表明，SOPC-APF有效解决了人工势场法不适用于多障碍物复杂环境的问题，以及传统算法容易陷入陷阱区域和局部极小点问题。下一步将考虑对于动态环境和突发情况下，机器人如何进行实时避障，为路径规划的真实性和适用性做近一步的研究。