多策略蚁群算法在机器人路径规划中的应用

刘双双，黄宜庆

1.安徽工程大学 高端装备感知与智能控制教育部重点实验室，安徽 芜湖 241000

2.安徽工程大学 安徽省电气传动与控制重点实验室，安徽 芜湖 241000

路径规划[1]指的是在环境中具有若干障碍物时，从起点开始，规划出一条到终点的有效安全路径，该路径需要具有转折点少、长度短等特点。目前使用的规划方法有A*算法[2]、人工势场法[3]、粒子群算法[4]、遗传算法[5]、蚁群算法[6]、深度强化学习[7-8]等。

蚁群算法因其具有较好的环境适应性和鲁棒性且便于融合其他算法的优点而广受关注。但蚁群算法随机性较强，易发生陷入死锁、规划路径非最优以及收敛较慢等问题。针对这些问题，不少学者也提出了相关优化方案。文献[9]中设置了一个菱形区域，并增加其内部的初始信息素含量来提高算法前期搜索效率，但是菱形区域内的信息素浓度没有区别，提高效果有限，且其奖惩策略会降低解的多样性影响得到最优解。文献[10]中增大了蚂蚁的视野范围，增加蚂蚁可行节点数来减少路径长度，但是蚂蚁的可行节点数量过多会增加算法的不确定性，且运行环境单一，未体现出算法的适应能力。文献[11]先是用基本蚁群算法得到全局路径后，根据全局路径外扩一定空间再利用蚁群算法寻找局部路径最优路径，若局部寻优得到路径更短，则更新该路径信息素，该方法虽增大了找到最优路径的概率，但是由于外扩空间的局限性依旧会陷入局部最优。文献[12]扩大了蚂蚁搜索范围，用向量夹角作为启发信息并引入了转移概率控制参数，虽然提升了算法的寻优性和收敛性，但是算法最终得到的路径并非最佳。文献[13]构建了全局优选区域，提高该区域初始信息素指导蚁群初期搜索，利用局部分块优化策略更新信息素，引入了信息素增强因子和反向学习策略，算法属性虽提升却有限，且有的路径出现回折情况。文献[14]将信息素释放在路径节点上，用先验方位引导策略和交替双向引导策略来提高蚁群探索能力和速度，有效提升算法对复杂障碍物分布大规模地图的求解能力，但算法结构的复杂度较大。

本文针对栅格环境下的路径规划问题提出一种新的改进方法，首先利用经过加权处理的A*算法启发函数对初始信息素进行非均匀化处理，使得算法前期的蚂蚁拥有一定的方向分辨性，减少无效搜寻；采用定向邻域扩展策略，扩大蚂蚁的方向选择性，提高搜索效率并缩短路径长度；在状态转移概率中增加角度引导因子以及障碍物影响因子，前者增大目的点的引导能力，加快算法中解的建立速度，后者为降低蚂蚁陷入死锁以及因下一步路径点选择不当而出现的曲折路径的概率；在更新信息素时，利用双重精英思想更新最佳路径上的信息素含量，加大蚂蚁找到最佳路径的可能，同时也可以加快迭代的收敛。

1 问题描述

1.1 环境模型的建立

为了在地图上体现出环境的相关特征，从而更加合理有效地规划出路径，对相关环境地图栅格化处理。其中，障碍物用黑色栅格表示，自由区域用白色栅格表示。首先，对环境中存在的障碍物，以机器人的尺寸半径将障碍物向外膨胀一定距离，如图1（a）所示，黑色三角形表示障碍物的原始状态，灰色表示膨化部分。之后将地图栅格化，若出现部分栅格中存在障碍物未占满整个栅格的情况，为便于算法运行，也将其认为是障碍栅格，如图1（b）。

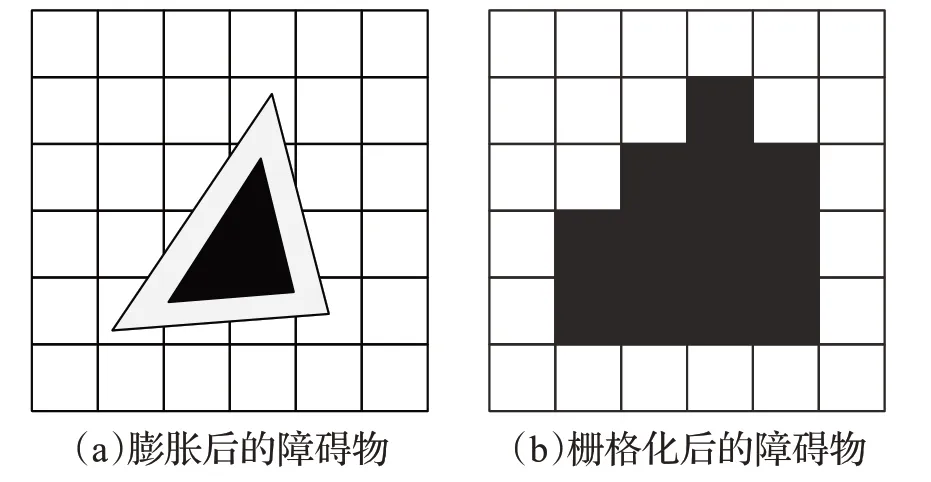
图1 障碍物膨胀示意图Fig.1 Schematic diagram of obstacle expansion

在静态的栅格地图中，采用蚁群算法规划路径时，先输入地图环境矩阵。其中，矩阵中元素1表示障碍栅格，元素0表示空白栅格，可让机器人通行。栅格的编码顺序为：由最上行最左列编号为1开始，向右依次编号到达边界后，再对下一行按照从左到右的顺序继续编码，直至每个栅格都有自己的序号为止。将地图左下角设为原点O，横坐标由左向右依次增大，纵坐标由下到上依次增大。栅格坐标和序号的对应关系如式（1）所示：

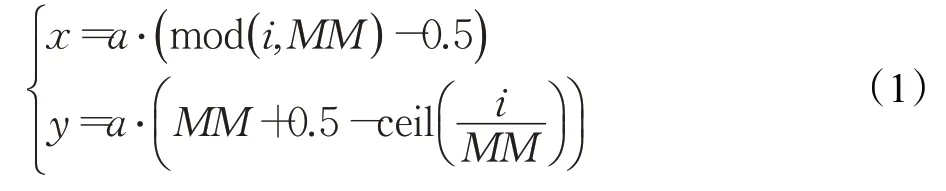
其中，x为栅格中心点的横坐标，y为其纵坐标；a为栅格边长，设为1 m；i表示栅格序号；MM表示地图中栅格的行数；mod()为求余函数，ceil()为向上取整函数。

1.2 原始蚁群算法

学者从自然中蚂蚁寻找食物的过程获得了灵感，创造出了蚁群算法。其原理是在寻找食物的过程中，蚂蚁在走过的路径上会释放信息素，后续的其他蚂蚁会比较各路径上的信息素量，倾向选择信息素更高的路径。

原始蚁群算法中，采用状态转移公式进行路径选择，该公式为：

在算法中，蚂蚁在走过的路径上遗留一定量的信息素，同时，路径上先前存在的信息素也会不断地蒸发消失，如此，信息素在越短的路径上越多，最佳路径被蚂蚁找到的可能性越大。此过程中，需要不断地更新信息素，更新方法为：

式中，τij(t+1)为更新后的路径(i,j)信息素浓度；ρ是信息素挥发系数，n是蚂蚁数目，Q是信息素增量，为一常数值；Lm为蚂蚁m所走的路径长度。

2 多策略蚁群算法

2.1 初始信息素非均匀化分布策略

在求解过程中，蚂蚁进行路径选择的主要依据之一是栅格间路径的信息素含量多寡。原始蚁群算法中，各栅格间路径的初始信息素分布均匀，为一个常数值。在算法初期，蚂蚁的启发函数值将决定状态转移概率的大小，依其计算方法可知，不同栅格的启发函数值差异很小，在没有信息素引导的情况下，蚂蚁搜索的盲目性大，搜索所得解的质量低，收敛速度慢。对栅格间路径的初始信息素进行非均匀化处理，有利于提升解的质量和加快算法的收敛速度。采用A*算法的启发函数思想，差异化处理不同栅格间路径的信息素，根据其在地图中的坐标赋予相应的信息素浓度，计算过程如下：

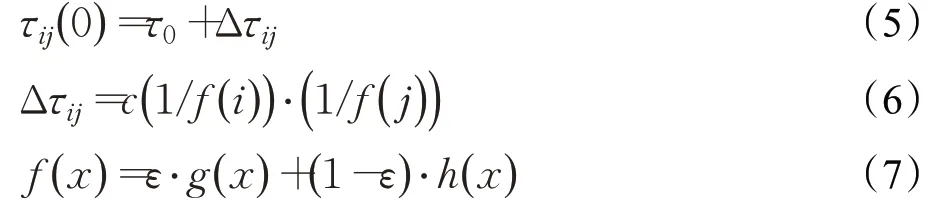
式（5）中，τ0为原初始信息素值，Δτij为另外在(i,j)路径添加的信息素；式（6）中，c为常数值，根据经验值以及栅格规模取值，f(i)和f(j)由式（7）计算得到；式（7）中，ε为加权值，g(x)为起点和当前点的间距，h(x)为当前点和终点的间距。

依据两点之间直线最短的距离可知，蚂蚁经过的路径越靠近起终点连线，该路径越优，当下一步待选栅格越靠近终点，路径越优，因此，ε应取较小值使终点起主导作用。此外，为算法的整体效果考虑，非均匀信息素值差距若过大，会造成算法过早收敛导致局部最优问题的出现，若过小，则该策略所起作用有限。因此，多次对c和ε的取值进行实验比较，确定最终取值为：c=2×4×4=32,ε=0.1。

2.2 定向邻域扩展策略

在基于栅格地图的原始算法中，蚂蚁只能够在其周围的相邻四个或者八个栅格选择下一步路径节点，搜索方向有限，因步长的限制所找到的最优路径长度也较长。文献[12]将蚂蚁的搜索方向扩展到16个，将蚂蚁的最小转角降低到了22.5°，有效扩大蚂蚁搜索范围以及缩短路径长度，但是也在某种程度上提高了算法的计算量。引入该扩展邻域的思想，根据地图起点和终点的相对位置，对邻域进行定向扩展，如图2所示。

图2中，S为起点，E为终点，i表示机器人当前位置。实线代表原始蚁群算法的可行栅格，虚线代表定向邻域扩展之后增加的可行栅格。采用定向邻域扩展策略不但能够丰富蚂蚁的搜索方向，达到通过一次搜索找到更短路径的目的，而且可以降低算法的计算量，加快算法的运行。由于改进算法中蚂蚁的可搜索栅格范围的增加，对蚂蚁的搜索方式进行重设。

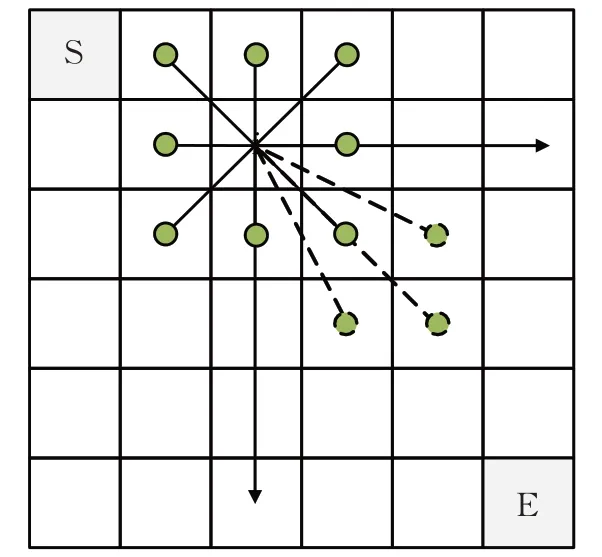
图2 定向邻域扩展后的可行栅格Fig.2 Feasible grid after directional neighborhood expansion

在当前栅格的周围八个栅格中，蚂蚁不可选择障碍栅格作为下一步的移动路径节点，在扩展得到的邻域栅格中，蚂蚁移动规则如下：若A或者C栅格中至少存在一个障碍栅格，蚂蚁不可从当前节点I直接移动到节点D；若B或者C栅格中至少存在一个障碍栅格，蚂蚁不可从当前节点I直接移动到节点J；若C栅格是障碍栅格，蚂蚁不可从当前节点I直接移动到节点K。如图3，C为障碍栅格，则蚂蚁无法从I直接移动到节点D、J、K中的任一节点。

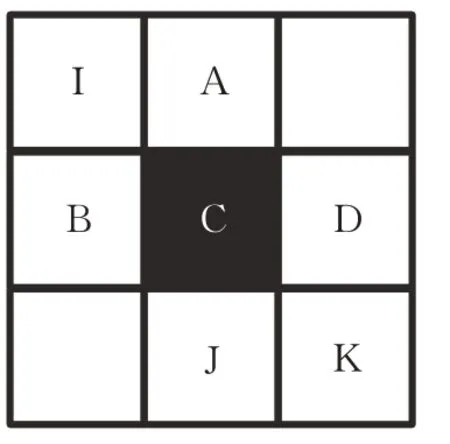
图3 定向扩展邻域移动情况分析Fig.3 Analysis of directional expansionneighborhood movement

2.3 状态转移概率公式改进策略

2.3.1 角度引导因子

在原始蚁群算法中，状态转移公式主要由启发函数和信息素含量两者组成。在算法初期，由于相邻栅格和终点之间的距离差异不明显，蚂蚁往往无法做出正确的选择导致解的质量差，搜索到最优路径的速度较慢。引入角度引导因子，可有效增加终点坐标对蚂蚁的引导作用，在保证蚂蚁具有足够大的搜索范围情况下，驱动蚂蚁向较佳方向进行搜索，使得蚂蚁可以更快到达终点。

角度引导因子定义：i为蚂蚁的当前栅格，其坐标为(ix,iy)；j为下一步可以到达的栅格，坐标为(jx,jy)；E为终点栅格，坐标为(Ex,Ey)。θij=∠jiE为角度引导因子中的角度，该角度的范围为[ ]0,180°。由于角度差值较大会影响状态转移公式计算，因此取角度的余弦值进行归一化处理后作为角度引导因子[12]νij，定义为：

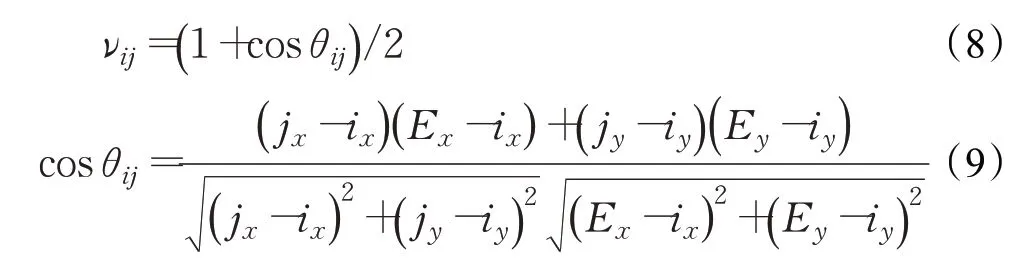
角度引导因子νij的函数变化图像如图4所示，角度影响因子值越接近1，说明蚂蚁下一步前进方向越贴近理想搜索方向，搜索效果越好。

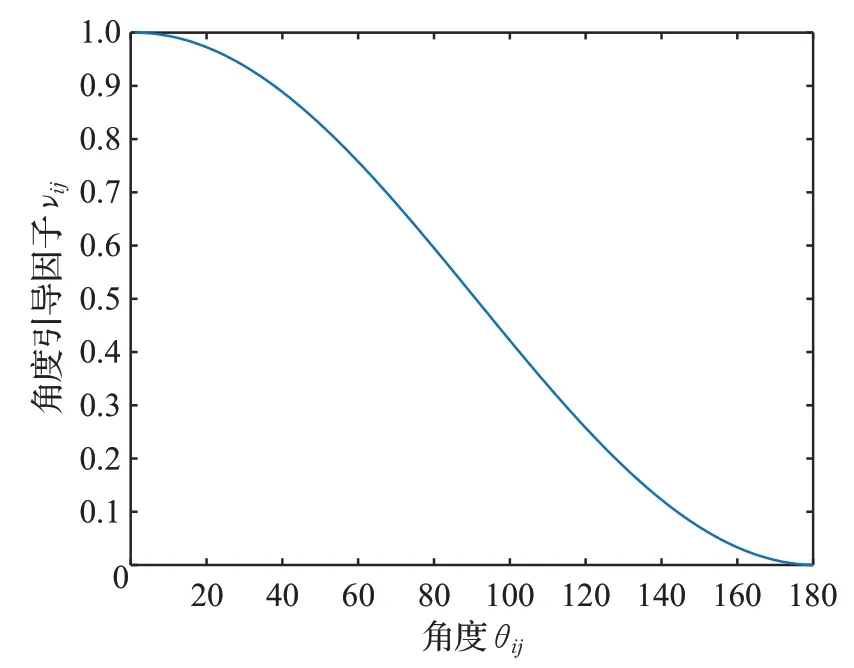
图4 角度引导因子变化趋势Fig.4 Change trend of angle guidance factor

2.3.2 障碍物影响因子

在路径规划中，障碍物的位置和分布情况也会对路径寻优产生极大的影响，原始蚁群算法并未对障碍物造成的影响进行分析并做出对应策略。如图5，令蚂蚁下一步潜在移动节点为j，若栅格4、5、6为障碍栅格，则会造成路径曲折；若栅格j周围栅格存在连续6个栅格为障碍栅格，则会极大增加蚂蚁陷入死锁的概率。一些改进算法从人工势场算法中得到启发，将障碍物斥力思想引入算法中，得到了很好的规划效果。为防止曲折路径和死锁的发生，引入障碍物影响因子Oifj(t)定义如下：

图5 障碍物影响因子设定示意图Fig.5 Schematic diagram of obstacle impact factor setting

障碍物影响因子的引入可有效降低路径曲折的概率，有效避免蚂蚁陷入死锁情况的发生，使得算法规划得到的路径更合理。

综上所述，在原始蚁群算法的基础上增加角度引导因子和障碍物影响因子，计算如式（8）～（10）所示，改进后的状态转移概率为

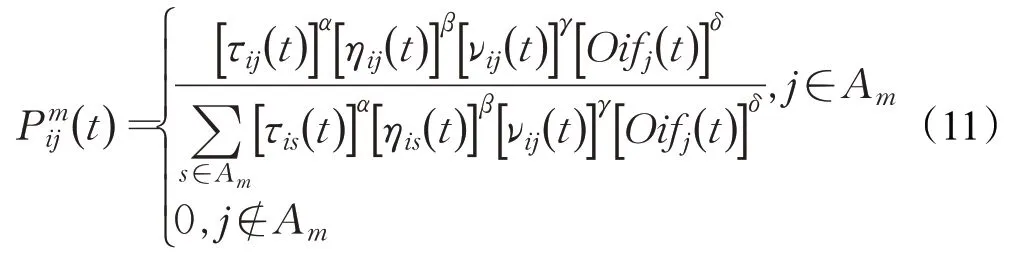
式中，除原始蚁群算法相关参数含义不变外，νij(t)表示t时刻的角度引导因子，γ为其重要程度；Oifj(t)表示t时刻的障碍物影响因子，δ为其重要程度。

2.4 双层精英蚁信息素更新策略

所有路径上的信息素部分挥发过程和蚂蚁在走过的路上留下新的信息素过程共同构成了信息素更新。但是原始蚁群算法中，算法中后期由于各路径长度差异不大，可能会出现不同长度路径上具有大致相同的信息素浓度，导致算法寻优速度过慢或者无法搜寻到最佳路径。为解决该问题，引入精英思想[15]，对每次迭代过程中的最优路径额外增加部分信息素，增强该路径对后面蚂蚁的引导作用。同时，该思想的引入有可能会造成算法收敛震荡，即因蚁群算法的随机性较强，会出现前一次迭代已经找到最优路径，但是因部分蚂蚁在一些次优路径片段上留下的信息素浓度叠加后高于最优路径，后一次迭代陷入局部最优，此类情况反复出现造成收敛震荡。为此，再次引入精英思想，对本次迭代最佳路径和历史迭代中的最佳路径进行长度对比，若前者长于后者，则加大历史最佳路径上的信息素含量。根据该信息素更新法的特点，将其称为双层精英蚁信息素更新策略，计算如下式：

3 改进算法的执行步骤

步骤1建立栅格地图的0-1矩阵，确定蚂蚁起点栅格S和终点栅格E；将算法中所有参数初始化：迭代次数K，单次迭代蚂蚁数量M，启发因子β，信息素因子α，信息素挥发因子ρ，信息素初始值τ0，信息素强度值Q、Q1以及Q2。

步骤2利用加权处理的A*启发函数对初始信息素值进行非均匀处理，根据公式（6）、（7）计算每段栅格路径的信息素增量Δτij，根据式（5）计算出栅格地图的信息素初始值τij(0)。

步骤3将M只蚂蚁放在起点栅格S中，首先将每只蚂蚁的禁忌表清零，设置路径点集合为空，路径长度为零。将起点加入禁忌表，根据起始点相对位置在当前栅格位置进行定向邻域扩展，根据式（8）～（10）计算下一步可行栅格点的角度引导因子及障碍物影响因子。

步骤4根据式（11）算出下一步每个可行栅格的状态转移概率，利用轮盘赌策略确定蚂蚁下一步栅格，更新该蚂蚁的禁忌表。

步骤5判断蚂蚁有无到达终点。若没有到达终点，则返回执行步骤3和步骤4，直到蚂蚁到达终点，否则执行步骤6。

步骤6当该次迭代中所有蚂蚁均完成搜索后，利用双层精英蚁信息素更新策略对所有成功抵达终点的蚂蚁经过的路径更新信息素。

步骤7判断迭代次数是否等于最大次数K，若等于，则输出最优路径及迭代曲线，若不等于，将迭代次数加1，再次执行步骤3到步骤6。

算法流程图如图6所示。

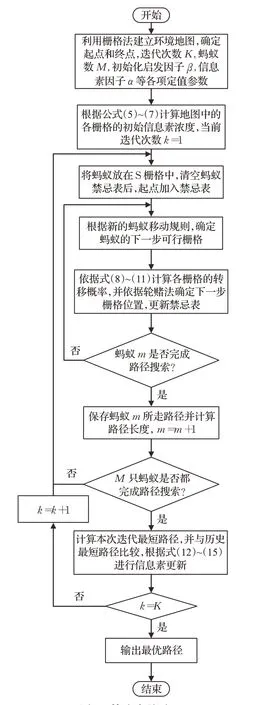
图6 算法流程图Fig.6 Flow chart of proposed algorithm

4 仿真实验及分析

通过仿真实验对本文改进蚁群算法的相关性能进行验证分析，选取障碍物分布不同的20×20和30×30的栅格地图各两个，对本文的多策略蚁群算法进行仿真，并且与原始蚁群算法以及其他的改进算法对比。仿真实验所需的运行环境：操作系统Windows 10（64位），处理器Inter®CoreTMi5-7200U，CPU 2.5 GHz，内存12 GB，仿真平台Matlab R2018a。

4.1 算法仿真参数的选取

蚁群算法中各参数的设值对算法性能影响颇大，为得到合理的参数值组合，采用试凑法对多组参数进行实验对比，选择较优值作为实验用值。本文依据经验法对算法中的主要参数在其变化范围内分别取5个不同的值，以一组默认参数组合为基准，每次只改变其中一个参数的值，为保证参数的合理性，进行10次仿真取平均值作为最终结果，仿真环境为障碍分布相同的20×20栅格地图。通过对实验结果的对比，取每个参数的最优值作为本文实验的参数参考值。

默认参数组合：α=1,β=1,γ=3,δ=3,ρ=0.4。各参数变化值：α∈{0.5,1,1.5,2,2.5},β∈{0.5,1,1.5,2,2.5},γ∈{1 ,3,5,7,9},δ∈{1 ,2,3,4,5},ρ∈{0.2,0.4,0.6,0.7,0.8}。实验中每次只改变一个参数值，其他参数值为默认值，所得实验结果如表1。

由表1可知：α的最优值在1附近，β的最优值在1附近，γ的最优值在5附近，δ的最优值在3附近，ρ的最优值在0.6附近。

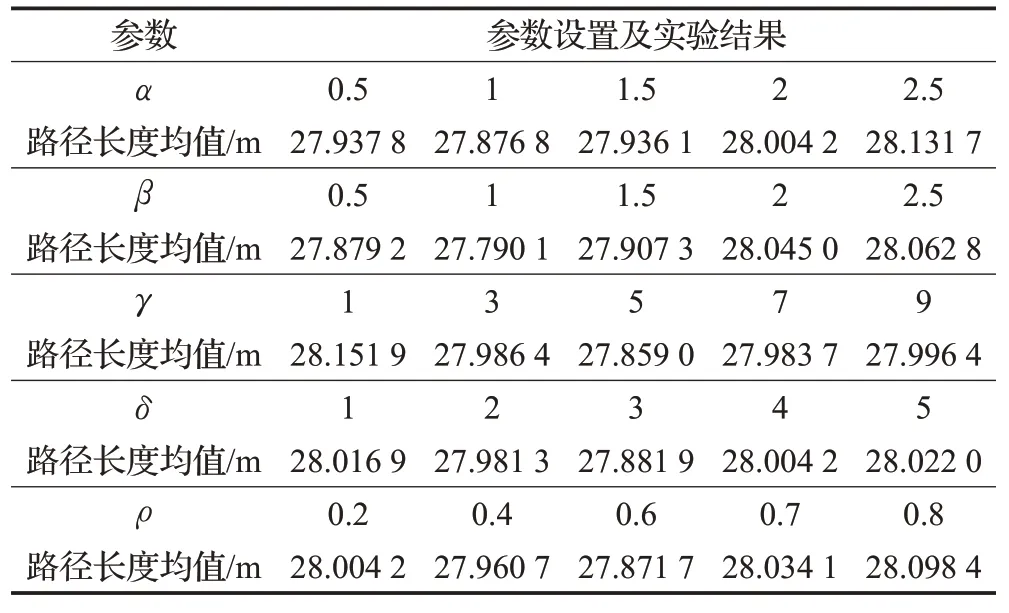
表1 主要参数测试实验结果Table 1 Test results of main parameters

Q为基础信息素强度，设为基础值1，Q1和Q2是在最优路径额外增加的信息素强度，经多次实验验证，Q1=1.2,Q2=4为宜，算法收敛速度较快且局部最优概率低。算法的具体参数设置如表2所示。

表2 仿真参数参考值Table 2 Reference value of simulation parameters

4.2 20×20栅格地图仿真实验

分别采用文献[13]和文献[16]中规格为20×20的两个障碍物分布不同的栅格地图中，对原始蚁群算法和本文的多策略蚁群算法进行仿真，并与文献[13]和文献[16]中的相关改进算法仿真结果进行对比。

4.2.1 与文献[13]算法和原始蚁群算法仿真对比

采用文献[13]的栅格环境，利用原始蚁群算法及本文改进算法进行仿真实验，结果如图7所示，与文献[13]的数据对比如表3所示。

图7 算法仿真结果对比图Fig.7 Comparison of algorithm simulation results

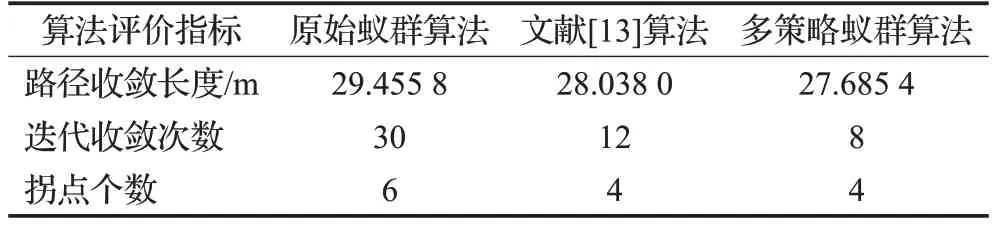
表3 算法仿真结果数据对比Table 3 Comparison of algorithm simulation results data

由表3可知，原始蚁群算法的路径长为29.455 8 m，文献[13]算法的路径长为28.038 0 m，本文的多策略蚁群算法的路径长为27.685 4 m，相较前两种算法，本文算法所得路径更短更平滑，在迭代收敛方面，本文算法只需8次即可收敛于全局最优路径，优于原始蚁群算法的30次和文献[13]算法的12次，在局部最优方面，原始蚁群算法在寻找到最优路径后依旧收敛于局部最优解，而本文由于双层精英蚁策略并未发生此类情况。由仿真结果对比得出，多策略蚁群算法的寻优性和收敛性更好。

4.2.2 与文献[16]算法和原始蚁群算法仿真对比

采用文献[16]的相应栅格地图再次进行仿真比较以验证算法的环境适应能力，结果如图8所示，路径规划仿真数据对比如表4所示。

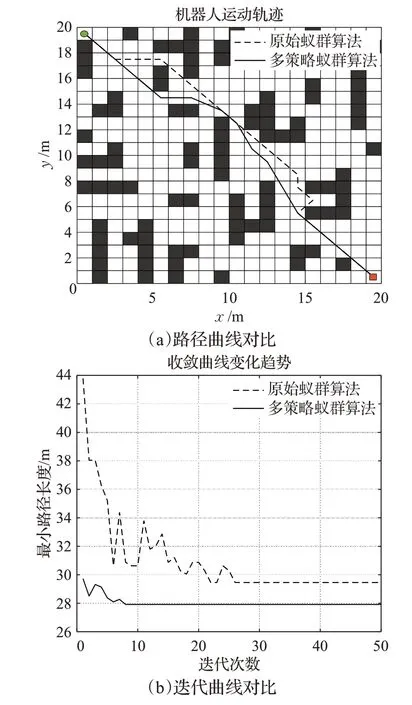
图8 算法仿真结果对比图Fig.8 Comparison of algorithm simulation results

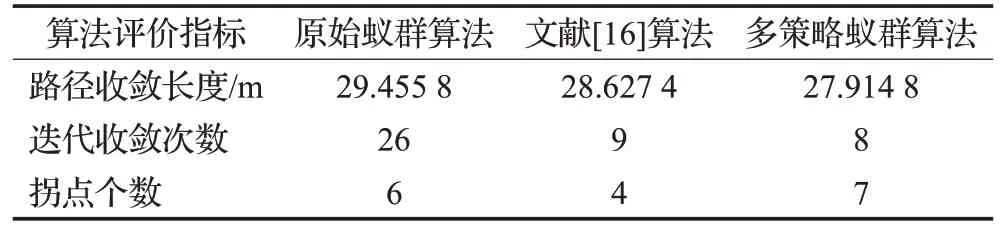
表4 算法仿真结果数据对比Table 4 Comparison of algorithm simulation results data

由表4可得，本文的多策略蚁群算法的路径收敛长度小于其他两种算法所得路径长度，迭代收敛速度高于原始蚁群算法及文献[16]算法，仅在拐点个数上由于移动规则和障碍物分布的原因，略高于另两者算法。因此，本文算法的寻优性较其他算法，有很大的改善，且收敛更快。

4.3 30×30栅格地图仿真实验

扩大栅格地图的规模，分别采用文献[13]和文献[12]提供的30×30栅格地图进行路径规划。同时，与原始蚁群算法和相应栅格地图的文献改进算法进行对比。

4.3.1 与文献[13]算法和原始蚁群算法仿真对比

采用文献[13]中的30×30规模的栅格地图，利用原始蚁群算法和本文算法进行路径规划，如图9所示，并与文献[13]算法所得仿真结果进行数据对比，如表5。

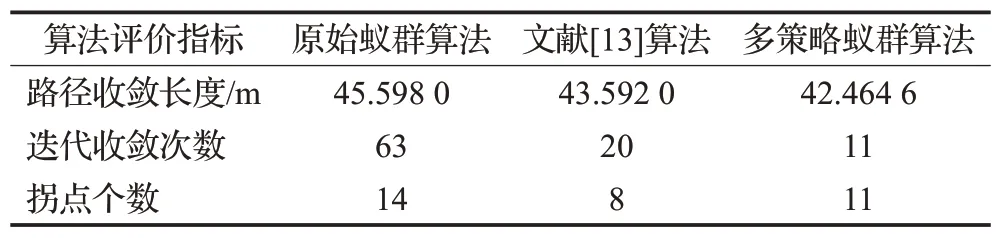
表5 算法仿真结果数据对比Table 5 Comparison of algorithm simulation results data

根据图9的对比图可知，与原始蚁群算法比较，本文算法在路径寻优方面以及收敛性方面都有了很大的提升。原始蚁群算法会出现路径曲折的问题导致路径长度加长以及转折角过小导致路径平滑度低的情况，而本文的多策略蚁群算法并没有此类情况。根据表5的仿真数据对比可知，多策略蚁群算法得到的收敛路径长度为42.464 6 m，小于其他两种对比算法的45.598 0 m和43.592 0 m，收敛速度也是最快的，仅需要11次即可收敛于最优路径，在拐点方面，本文算法得到11个拐点，少于原始蚁群算法拐点数14个，多于文献[13]算法的8个拐点，路径平滑度也具有一定的改善。从综合指标方面考虑，在30×30栅格地图中，本文的多策略蚁群算法也具有较好效果。

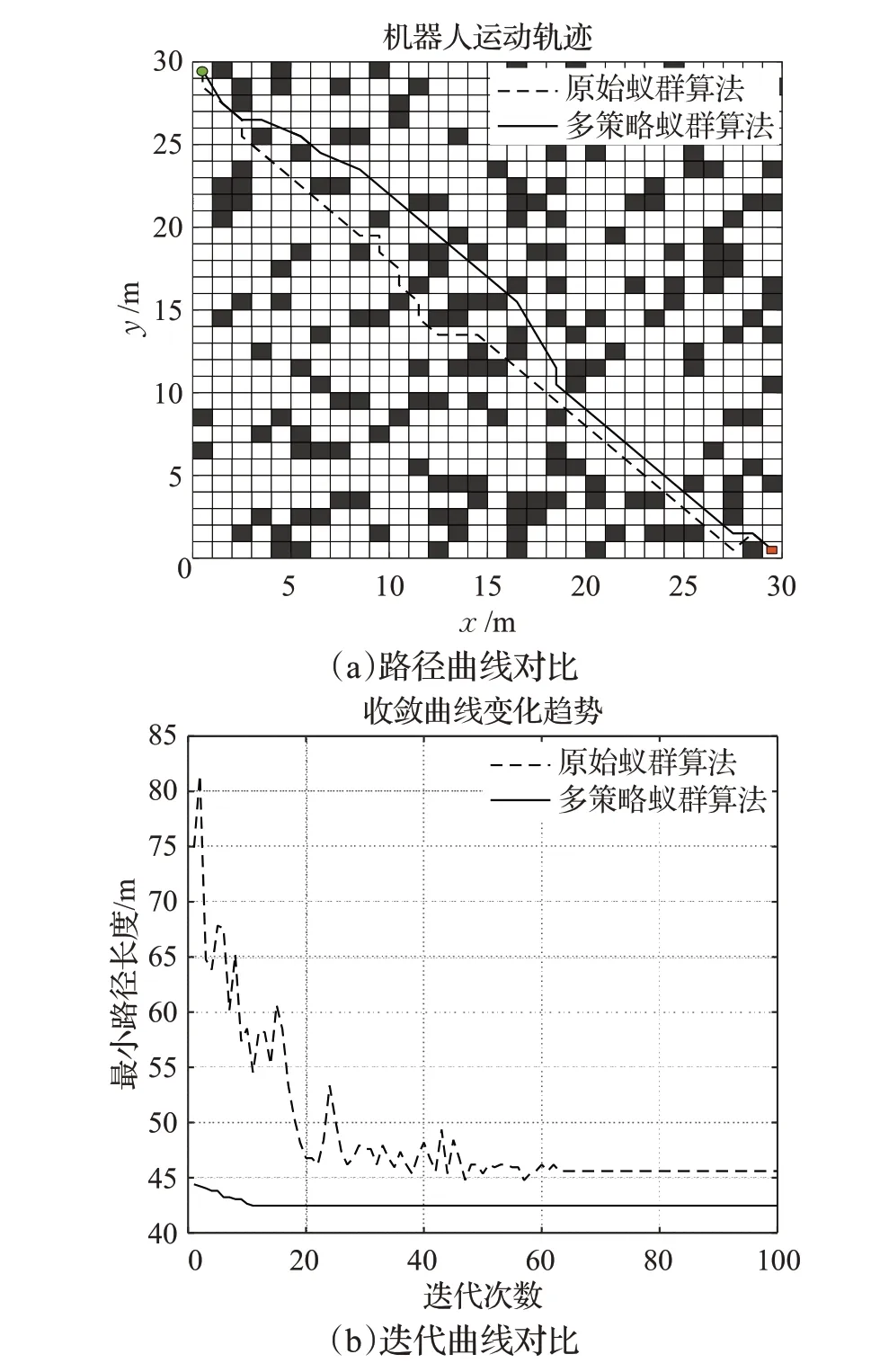
图9 算法仿真结果对比图Fig.9 Comparison of algorithm simulation results

4.3.2 与文献[12]算法和原始蚁群算法仿真对比

根据文献[12]中的30×30栅格地图，利用本文多策略蚁群算法和原始蚁群算法比较仿真结果，如图10所示。同时，选取文献[12]算法中路径长度为最优值的仿真结果作数据对比，如表6所示。

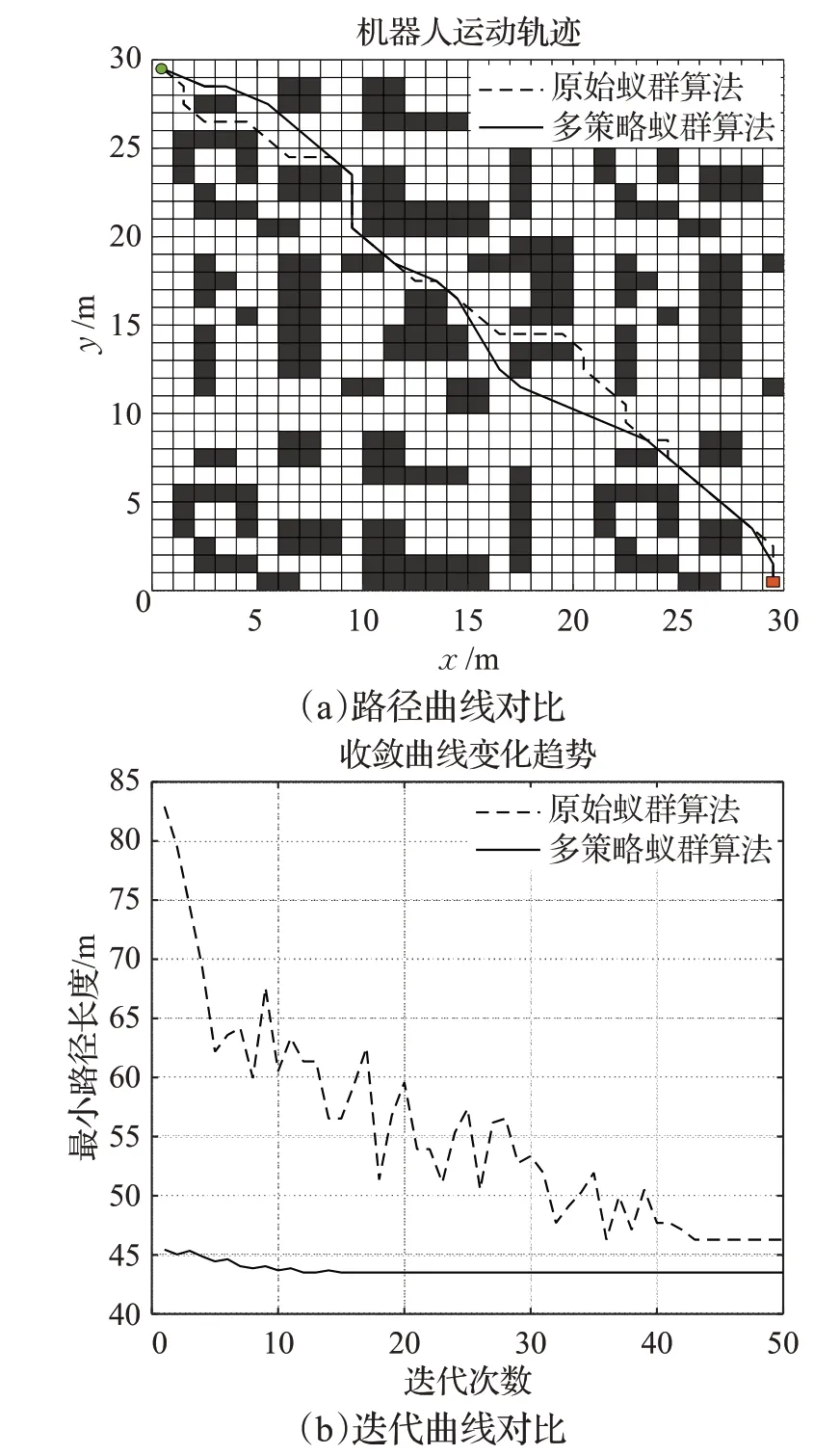
图10 算法仿真结果对比图Fig.10 Comparison of algorithm simulation results

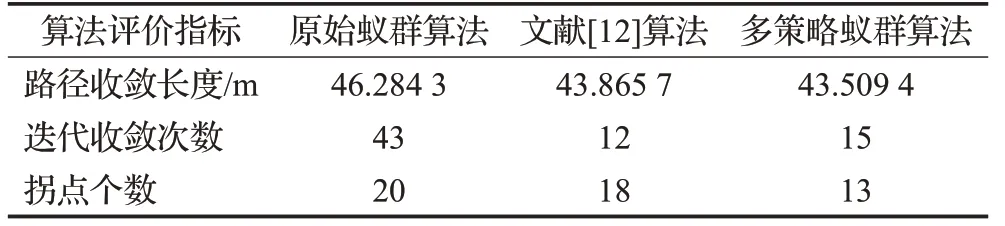
表6 算法仿真结果数据对比Table 6 Comparison of algorithm simulation results data

为进一步和文献[12]算法进行对比以验证本文算法优越性，在该栅格地图中利用本文算法共进行10次仿真实验，本文多策略蚁群算法迭代过程如图11所示。其相关数据对比如表7。

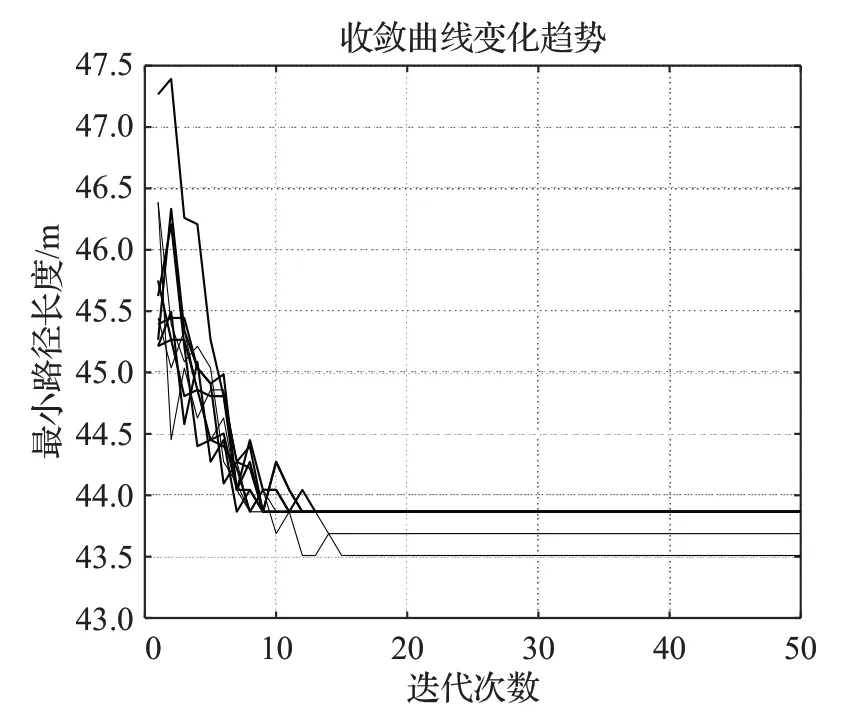
图11 10次仿真结果迭代图Fig.11 10 iterations of simulation results

由表6中数据可知，文献[12]算法和本文的多策略蚁群算法的各项指标均优于原始蚁群算法。从表7可知，本文算法搜索得到的最优路径长度为43.509 4 m，小于文献[12]算法的最优路径长度43.865 7 m。并且，本文算法10次仿真中搜索得到的所有路径长度均不大于文献[12]算法的任何一次仿真路径长度，其平均路径长度和平均迭代次数也都优于文献[12]中提出的算法。因此，该对比结果再一次地验证了本文的多策略蚁群算法具有较强的寻优能力和收敛能力。

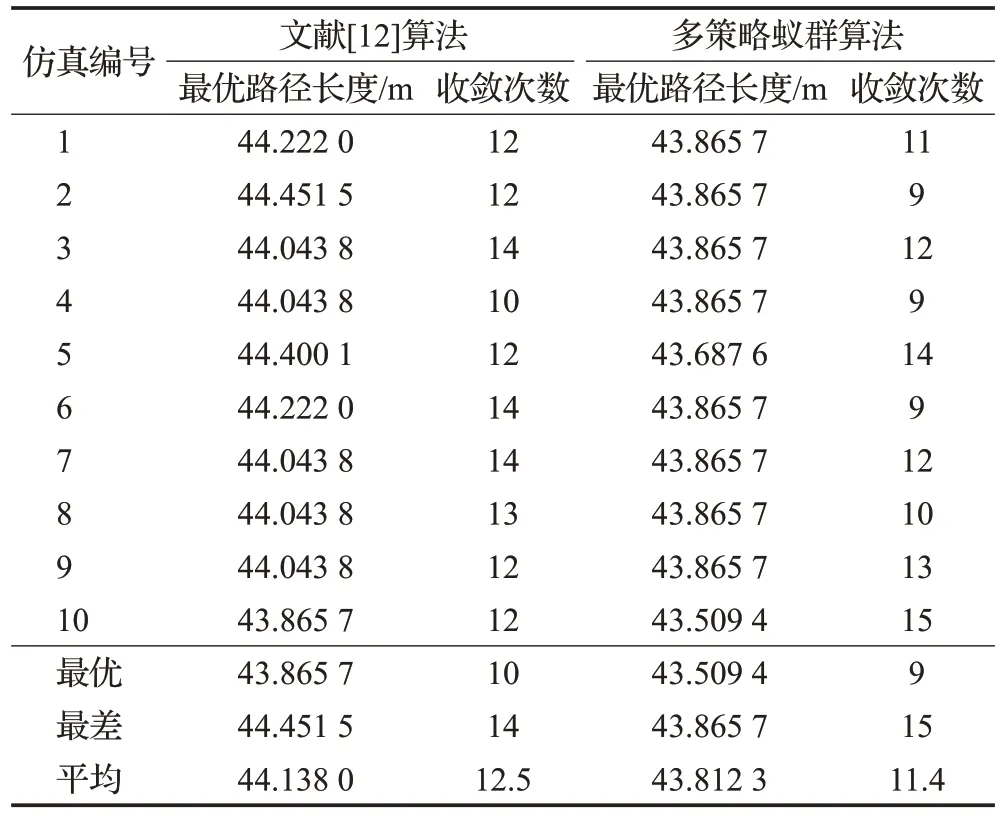
表7 10次迭代仿真数据对比Table 7 Comparison of simulation data of 10 iterations

5 结束语

针对原始蚁群算法在较复杂环境中容易陷入次优路径，找寻不到最优路径，搜索得到的路径因蚂蚁的移动规则束缚导致过长以及收敛过慢等问题，提出多策略蚁群算法。首先依据栅格所在位置利用加权的A*启发函数进行计算，额外增加该栅格的初始信息素，提高算法收敛速度；其次，利用定向邻域扩展策略增加蚂蚁的可行栅格数量，加快蚂蚁向终点搜索的速度；之后，利用角度引导因子和障碍物影响因子改进状态转移概率公式，驱使蚂蚁向有效方向进行搜索并减少曲折路径和死锁蚂蚁出现的概率；最后，采用二次精英蚁策略对路径上的信息素进行更新，加强较优路径对蚂蚁的引导作用，提高蚂蚁的全局搜寻能力，避免局部最优的产生。仿真实验结果表明，本文找到最佳路径所需的迭代次数更少，即收敛更快，找到的路径更短，即寻优性更好。