动态栅格划分的光线追踪场景绘制

陈滨，虞鸿，吴哲夫

(1.浙江工业大学 艺术学院，浙江 杭州 310023;2.浙江工业大学 信息工程学院，浙江 杭州 310023)

在光线追踪绘制真实场景过程中，加速结构是用来减少光线-图元相交检测所需要的时间［1］.早期提出的加速结构包括Bentley提出的kd树［2］，Rubin和Whited提出的 BVH［3-4］，以及 Fujimoto提出的均匀栅格法［5-6］，Sachidhar等人已经把这种算法在GPU上实现［7］.对于均匀栅格法的加速结构，它是将空间细分为具有相同大小的长方体形式的三维栅格.这种空间组织方式创建简单，主要就是把空间中的图元分配到关联的网格当中，因此它的建立速度要快于kd树和BVH，但是它的光线遍历并求交的速度要慢于kd树和BVH.对于动态真实场景的绘制，每种加速结构的效率是由两部分组成:加速结构建立时间和光线-图元求交时间.在真实复杂场景绘制的时候，由于场景中的图元分布未知，Wald等人认识到很难选择一种较为平衡的方法，最终提出了采用建立速度较快的相对比较平衡的grids方法来替代建立速度较慢的kd树和BVH等方法［8］.Shirley提出只对每个拥有图元的栅格构造对象［9］，拥有图元的栅格只存一个图元指针，该优化方法大大降低了该方法所需要的内存.然而，均匀栅格法在光线遍历的过程中还没有很好的提升，主要因为在类似由一个较小的物体和较大的房间组成的场景中，有许多没有涉及到实体的空间也会进行同样数量的栅格划分［10］.因此，这种方法就增加了许多冗余的光线与加速结构求交计算.

本文描述了一种改进后的均匀栅格方法，它根据每个栅格所包含的图元数量动态分割栅格，在那些比较空旷的空间就不进行栅格划分了，除去了因为没有必要的栅格划分而带来的多余计算量.最后，在CPU上实现动态栅格加速结构的光线追踪方法.

1 栅格数据结构

建立栅格数据结构过程包括把整个空间中所有物体的包围盒分割成大小相同的栅格(本文把空间中的一个长方体体元当作一个栅格)，并把组成物体的图元(一般为三角形)放入这些栅格中.在均匀栅格法当中，栅格的数量是根据整个空间中图元的个数决定的，每个维度的栅格数量nx、ny、nz可进行如下计算［11］:

式中:wx、wy、wz为空间中所有物体包围盒 x、y、z方向的跨度，m用来改变栅格数量的系数，通常取2，s为每个栅格的边长.由于它均匀地分割成相同大小的栅格，可将这些栅格根据对应的坐标序号放入一个一维数组当中，如图1.栅格数组中的每个栅格对象保存着指向与该栅格关联的三角形图元指针，若栅格没有关联的三角形图元，那么可以把这个栅格对象设置为空.

图1 均匀栅格法的空间划分和数据结构表示Fig.1 Uniform grids space partition and data struct presentation

动态栅格法的空间划分也是基于均匀栅格划分策略，但是动态栅格划分并不是一下子均匀地划分成相等大小的栅格，如图2.栅格树的根部代表整个空间所有物体的包围盒，每个子节点表示父节点进行一次均匀划分4个部分的子栅格.和均匀栅格的数据表示一样，每个栅格对象保存着指向与该栅格关联的三角形图元指针，若没有关联图元对象可以设置为空.栅格树有2个重要的性质:1)涉及多个栅格图元，它的指针可能会保存在多个栅格节点;2)树左侧节点中图元离视点距离一定小于树右侧节点中图元离视点的距离，并且随着树的深度变化，节点中的图元离视点的距离也越远.这样在光线遍历的过程中，如发现与某个图元相交，那么就结束该光线的遍历.

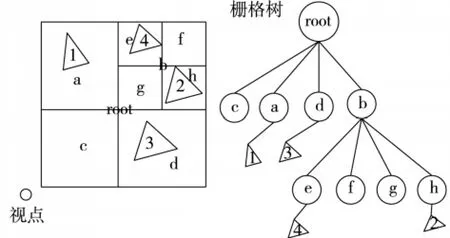
图2 动态栅格法的空间划分和数据结构表示Fig.2 Dynamic grids space partition and data struct presentation

2 基于视点距离的栅格建立

为了提高光线追踪中光线与栅格遍历速度，许多方法在建立加速数据结构的时候都进行了排序［12-13］.根据从顶层到底层的顺序建立栅格树，这个从顶层到底层的顺序对应着栅格节点中的图元距离从近到远.先把根节点初始化，对空间中所有物体的包围盒做一次均匀栅格划分，此次划分在x、y、z方向一分为二，即在三维空间中把物体包围盒分成8个栅格.然后根据离视点的距离，从左到右依次作为根节点的子节点.在本文的实现当中，视点放在z轴的负半轴上，因此栅格的z轴序列号较小的就是离视点较近的.最后判断这些子节点中的图元是否到达栅格的饱和状态，若没有到达栅格的饱和状态，那么用相同的方法继续划分子栅格，反之则停止.图3描述了一个栅格的饱和状态，左图中的栅格中有2个三角形图元a和b，如果对这个栅格再进行每个维度二分的栅格划分，那么它的每个子栅格还是关联着2个图元三角形，这样的重复操作将会消耗很大的递归栈空间，因此在实现当中，针对遇到这种情况就停止栅格划分.

图3 栅格的饱和状态Fig.3 Saturation state of the grid

如上所述的栅格数据结构构造方法，显然比较适合一些非规则分布的模型，例如当视点对着广阔的天空，天空中排布这零星的物体，这些物体相对天空就比较小.因此在天空这部分做栅格划分的时候，很快就到达了栅格饱和状态，而划分物体的时候会划分地比较密，算法1给出了本文的动态栅格划分方法.

算法1 动态栅格建立

输入:空间中三角形图元数组objects，这些图元的包围盒bbox，栅格根节点recursivecells

1)if recursivecells equal null then

2)初始化根节点的子栅格数，numcells=2×2×2，并把根节点recursivecells的8个子栅格都设置为null;

3)for each objectsi，do

4)objbbox=objectsi-＞bbox;

5)根据单个图元包围盒objbbox的位置，把它分配到父节点包围盒bbox其中8个子栅格当中，得到这个图元在父节点当中的3个维度最大最小序列号 cellminx，cellminy，cellminz，cellmaxx，cellmaxy，cellmaxz

6)for iz from cellminz to cellmaxz

for iy from cellminy to cellmaxy

for ix from cellminx to cellmaxx

7)获得子栅格序列号cellindex=ix+iy×2+iz×2;

8)if recursivecells［cellindex］equal null then

9)构造一个类型和根节点一样的栅格对象recursivecell，把 objectsi分配到 recursivecell

10)else then

直接把objectsi分配到recursivecell

11)for each recursivecelli

if recursivecelli has reached saturate state then break;

else then继续调用该函数;

3 动态栅格建立算法分析

算法1在实现动态栅格建立的过程当中采用函数递归的方法，必须考虑到算法效率和调用栈空间开销中寻求平衡.首先有以下假设:整个空间中图形元组成的包围盒是一个正方体，这个包围盒中有N(8的幂次数)个三角形图元;每个栅格的饱和状态为容纳一个三角形图形元.

算法1消耗的时间主要由均匀栅格划分时间、分配图元时间组成.无论栅格大小、均匀栅格划分时间Tgrid都是一样的.分配图元的时间与图元的数量成正比，Tprimitive为分配单位图元的时间.算法1中，最坏的情况就是每次栅格都分割为8个子栅格，用图4中的递归树分析可得，算法1在最坏情况下的消耗时间T为

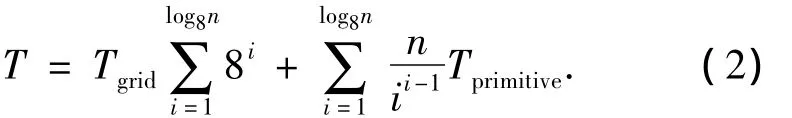
式中:i表示在递归树中的深度，根节点的深度为0.深度为i的子节点个数为8i，每个子节点中的图元数目为n/8i-1.进一步可得到化简式:

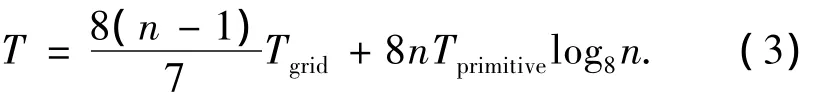
从式(3)可得算法1的时间复杂度为O(n)，与均匀栅格划分方法的时间复杂度是一个数量级别的［14］.

图4 算法1的递归树Fig.4 Recursive tree of algorithm 1

为了验证算法1的时间复杂度和均匀栅格划分的时间复杂度一致，在Intel i5 CPU，2 GB内存的PC机上进行实验，取4个不同大小的Stanford大学网站上的模型Bunny，其图元数量大约为4k、10k、16k、69k，分别测量栅格结构的建立时间.测量结果如表1所示.从表1中可以看出，本文方法的运行时间略慢于均匀栅格法，由前文分析可得，该方法需要对每个栅格判断是否处于饱和状态，然而均匀栅格法是不需要这些判断的.本文方法和均匀栅格法的运行时间增长趋势是一致的，说明该方法在建立栅格结构的运行时间是合理的.

表1 不同模型下均匀栅格法和本文方法的建立时间Table 1 Building time of uniform grid and our method by different models

4 基于动态栅格法的光线遍历

和均匀栅格光线遍历方法一样，每根光线只与它穿过的栅格内部图元做相交运算［15］.这比没有加速结构的时候能节省许多时间，特别是当场景中有大量物体的时候，光线只与其中一部分物体做相交运算.本文的光线遍历方法也继承了以上的优点，并对场景中存在较大空旷区域的情况进行了优化.

图5 一条光线的动态栅格结构遍历Fig.5 Dynamic grids struct traversal of a ray

图5所表示的就是一条光线穿越本文提出的动态栅格结构的情景.斜杠标记的栅格即光线穿越的栅格，光线将根据栅格与视点距离进行求交运算，顺序依次为(c，0)- ＞ (d，3)- ＞ (g，0)- ＞(h，2)- ＞(f，0).括号中的第1项为栅格编号，第2项为该栅格中的图元编号.第2章节中已经提到，本文的栅格划分方法就是基于栅格与视点的距离建立的.把这个顺序对应到图2中去，这个操作顺序是非常方便的，栅格树同一深度的子树，操作顺序一定是从左往右，不同深度的子树，操作顺序一定是从上往下，这在一定程度上增强了算法性能.

本文动态栅格结构光线遍历方法关键在于如何沿着光线方向依次遍历栅格，如图5，即如何沿着(c，0)- ＞ (d，3)- ＞ (g，0)- ＞ (h，2)- ＞ (f，0)该路径遍历栅格.观察到图5的动态栅格结构是把根节点均匀划分为a、b、c、d 4个栅格，然后再把b节点划分为e、f、g、h 4个栅格.因此可以对根节点采用均匀栅格的光线遍历方法，当检测到节点b时，再一次采用均匀栅格的光线遍历方法，即动态栅格结构光线遍历方法就是一种均匀栅格结构光线遍历方法的递归模式.

均匀栅格结构中为了沿着光线方向计算遍历步进，采用以下比较巧妙的方法.即使光线和栅格边的交点不是均匀的，如图6(a)，但是在x方向和y方向上的交点是均匀的，如图6(b)和图6(c).这样允许分别从x、y方向计算光线参数t，每个方向的光线参数t的步进为

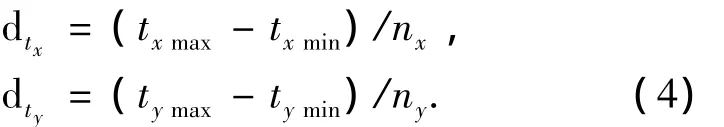
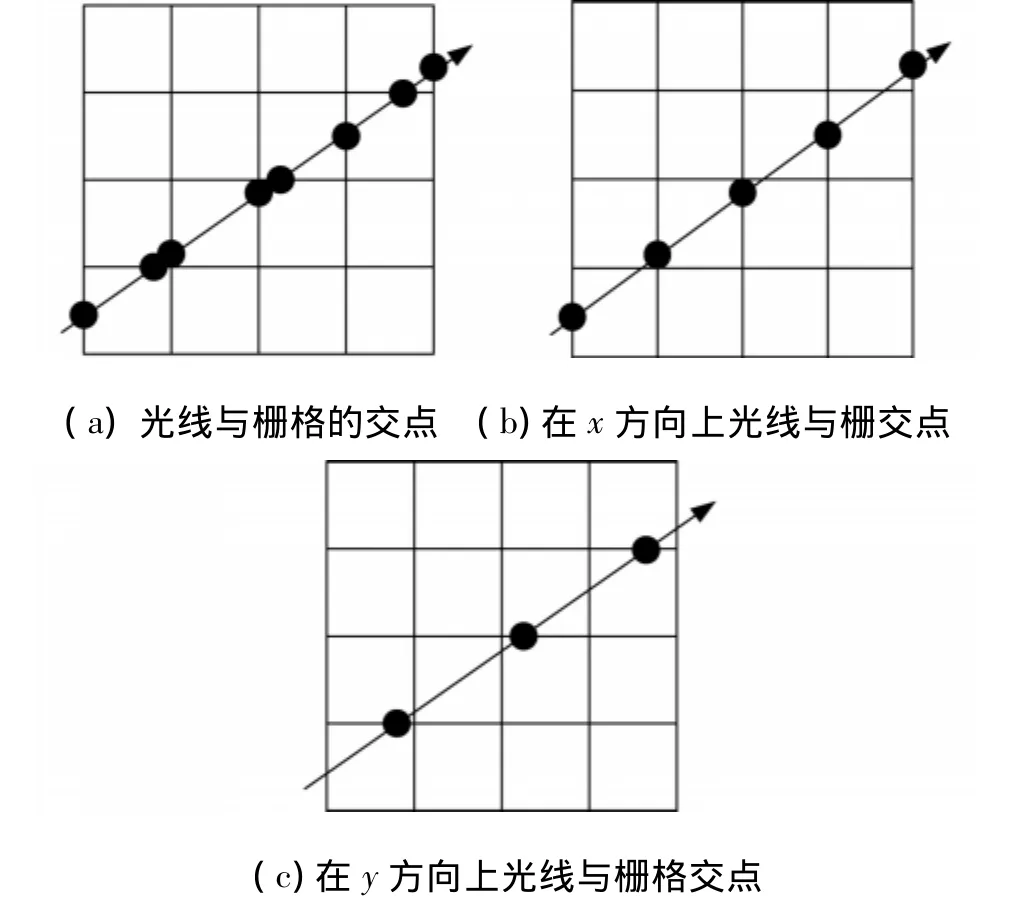
图6 每条光线的动态栅格结构遍历Fig.6 Dynamic grids struct traversal of every ray

针对每个栅格，必须算出下一个光线经过的栅格，在二维栅格的情况下，通过x方向步进和通过y方向的步进得到的下一个栅格是不一样的，图7说明了这2种不同情况，黑色的正方形就是应该选择的下一个栅格.在图7中，假设光线刚进入初始栅格时，在x方向最小的光线参数为tminx，在y方向最小的光线参数为tminy，横斜杠标记的栅格为当前进入的栅格，竖斜杠标记的栅格为下一个进入的栅格，计算txnext和tynext，它们分别为x方向和y方向的下一个光线经过栅格的光线参数.如果txnext＜tynext，就把x方向的下一个栅格作为光线下一个经过的栅格，反之把y方向的下一个栅格作为光线下一个经过的栅格.

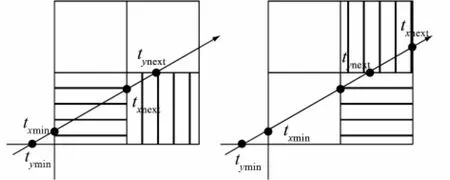
图7 决定下一个光线经过的栅格过程Fig.7 Process of next grid a ray pass through

本文的动态栅格光线遍历方法也是基于以上方法，它决定下一个光线经过的栅格之后，必须还要判断这栅格是否还有子栅格，如果有子栅格的话还需要重复上述过程，反之则检测这个栅格和图元的求交情况.算法2给出了本文光线遍历算法，为了简化算法描述，假设光线的起点位于空间所有物体的外面.

算法2 动态栅格光线遍历

输入:当前光线对象ray，光线参数tmin，当前父栅格的包围盒bbox，光线图元求交之后的信息hitrecord，栅格树 recursivecells.

1)初始化光线进入空间栅格区域每个方向的栅格序号ix，iy，iz;每个方向的栅格光线参数步进dtx=(txmax-txmin)/nx，dty=(tymax-tymin)/ny，dtz=(tzmax-tzmin)/nz;

2)计算出每个方向下一个栅格的光线参数，每次步进的栅格个数，已经遍历的最后的栅格序号.

算法2递归次数由某个空间区域的图元数量决定，数量少的区域很快完成递归，数量多的区域会进行多次递归.

5 动态栅格法光线遍历算法分析

与第3节分析动态栅格建立算法一样，采取相同的假设:整个空间中图形元组成的包围盒是一个正方体，这个包围盒中有N(8的幂次数)个三角形图元;每个栅格的饱和状态为容纳一个三角形图形元.

由算法2可知，光线遍历算法消耗时间由2部分组成:确定初始化栅格具体序号的时间、光线与它经过的栅格检测相交的时间.每条光线只需进行一次初始化栅格具体序号的确定，把这段时间定为Tinit，第2部分消耗时间则与空间内部具体图元分布有关，每个栅格求交时间为Tintersect.考虑最坏情况，即空间的图元是分布均匀的，那么空间动态栅格建立的子栅格也是均匀分布的，光线在这种情况下沿着对角线经过子栅格，并且光线到达最后一个子栅格才检测到与图元相交.对角线上的栅格数量也是与N有关，如图4空间中物体包围盒每个方向可以分成8log8N个栅格，那么物体包围盒最长对角线的数量Nray可以由式(5)得到.那么在最坏情况下，每条光线的遍历时间Ttraversal如式(6)所示.因此，本文算法计算复杂度为O((log8N)2/3).这个数量级和均匀网格遍历方法是一样的，但是在实际场景中，特别是针对空旷的场景性能是有明显提升的.式(6)只是给出了本文算法的估计的一个运行数量级时间，与实际往往有比较大的偏差，主要原因在于Tintersect这个变量在每个栅格中并不是都是一样的，可能在某些栅格它的饱和图元数量为c1，其他栅格的饱和图元数量为c2.这会影响光线与当前栅格的求交时间.

6 实验及结果分析

在Intel i5 CPU，2GB内存的PC机上进行了实验.实验以如下方式进行:选择若干典型模型，它们都处于由三角形图元组成的地面.分别对这些场景用均匀栅格法和本文提出的动态栅格法进行光线追踪，最后把这2种方法进行比较.

实验实用的模型包括多个不同大小的Bunny、Horse、Fish、Hand，为了体现空间的空旷性，在它们的下方放着由三角形图元组成的地面，图8为使用本文方法光线追踪绘制的模型图.实验一共分为2组，第1组使用均匀栅格方法并记录运行时间和划分的栅格数目.第2组使用本文提出的动态栅格光线追踪方法并记录相同的数据项目.表2给出了这些模型具体图元数目，采用2种方法的栅格划分数目以及这2种方法的运行时间.为了突出本文算法在空旷场景的作用，本次实验的模型包括三角形图元的地面，这样更加凸显出场景的空旷性.

图8 用本文方法光线追踪绘制的场景Fig.8 Scenes drawn by ray tracing through our method

实验结果如表2所示，采用本文提出的动态栅格光线追踪方法绘制场景确实提高了绘制速度.注意到Horse、Fish、Bunny4k的图元个数虽然远远小于其余的模型，但是绘制时间还是比较长，这是由于放大了渲染模型.可以看到，本文方法所需要的栅格远远小于均匀栅格所需要的栅格，这从算法的初衷就可以猜测到:采用均匀栅格结构光线追踪算法没有对模型进行任何判断，直接对场景按照式(1)进行均匀栅格划分，然后本文算法是根据场景的疏密程度动态地进行栅格划分，因此所需要的栅格会大大减少.表2中还可以看到不同图元的Bunny随着图元数量的增加本文方法的运行时间并没有减少，这和栅格划分数有关，在图元集中的区域栅格数量的增加是可以加速场景绘制速度的，从另一个角度说明本文算法随着场景图元疏密程度增加性能就越高.

表2 不同模型下均匀栅格法和本文方法绘制场景运行时间Table 2 Scene drawing time of uniform grid and our method by different models

7 结束语

对于光线追踪绘制场景的加速均匀栅格结构，本文提出了一种新的动态栅格加速结构.与已有的方法相比，本文的方法对需要绘制的场景根据不同分布特征进行按需栅格划分.在建立动态栅格加速结构的时候，不同深度从根节点到叶子节点，同一深度从左边节点到右边节点，都是随着离视点的距离逐渐增大，这有利于光线的遍历.实验结果表明，本文方法在处理空旷场景的时候，优于同类的已有工作，本文的方法还能推广到基于GPU光线追踪加速结构上，这也是未来将扩展的工作.

［1］ANDREW S.An introduction to ray tracing［M］.London:Academic Press，1989:201-204.

［2］BENTLEY J L.Multidimensional binary search trees used for associative searching［J］.Communications of the ACM，1975，18(9):509-517.

［3］RUBIN S M，WHITTED T.A 3-dimensional representation for fast rendering of complex scenes［C］//Proceedings of the 7th Annual Conference on Computer Graphics and Interactive Techniques.New York，USA，1980:509-517.

［4］KIRILL G，SIMON P，ALEXANDER B，et al.Grid-based SAH BVH construction on a GPU［J］.The Visual Computer，2011，27(6/7/8):697-706.

［5］TANAKA T，IWATA K.Arts:accelerated ray-tracing system［J］.IEEE Computer Graphics and Applications，1986，6(4):16-26.

［6］童星，袁道华.基于GPU和均匀栅格法的光线追踪算法研究［J］.计算机工程与设计，2011，32(10):3499-3502.

TONG Xing，YUAN Daohua.Research of ray-tracing algorithm based on GPU and uniform grid method［J］.Computer Engineering and Design，2011，32(10):3499-3502.

［7］GUNTURY S，NARAYANAN P J.Raytracing dynamic scenes on the GPU using grids［J］.IEEE Transactions on Visualization and Computer Graphics，2012，18(1):5-16.

［8］WALD I，IZE T，ANDREW K，et al.Ray tracing animated scenes using coherent grid traversal［C］//Proceedings of ACM SIGGRAPH.New York，USA，2006，485-493.

［9］SHIRLEY P，ASIKHMIN M，GLEICHER M，et al.Fundamentals of computer graphics［M］.2nd ed.Wellesley:AK Peters，2005:224-226.

［10］KALOJANOV J，BILLETER M，SLUSALLEK P.Two-level grids for ray tracing on GPUs［J］.Computer Graphics Forum，2011，30(2):307-314.

［11］KALOJANOV J，SLUSALLEK P.A parallel algorithm for construction of uniform grids［C］//Proceedings of the Conference on High Performance Graphics.New York，USA，2009:23-28.

［12］GARANZHA K，LOOP K.Fast ray sorting and breadthfirst packet traversal for GPU ray tracing［J］.Computer Graphics Forum，2010，29(2):289-298.

［13］PANTALEONI J，LUEBKE D.HLBVH:hierarchical LBVH construction for real-time ray tracing of dynamic geometry［C］//Proceedings of the Conference on High Performance Graphics.Switzerland，2010:87-95.

［14］VACLAV S.An efficient space partitioning method using binary maps［C］//Proceedings of the 11th International Conference on Telecommunications and Informatics.Wisconsin，USA，2012:121-124.

［15］PERROTTE L，SAUPIN G.Fast GPU perspective grid construction and triangle tracing for exhaustive ray tracing of highly coherent rays［J］.International Journal of High Performance Computing Applications，2012，26(3):192-202.