空泡螺旋桨诱导的双桨船脉动压力数值预报

叶金铭，熊鹰，孙海涛，王展智

(海军工程大学 船舶与动力学院，湖北 武汉 430033)

螺旋桨是船舶水下主要的振动和噪声源，对于高速舰船，螺旋桨空泡往往不可避免，空泡的产生会使螺旋桨脉动压力急剧增加，研究空泡螺旋桨脉动压力的预报方法，对于提高水面舰艇螺旋桨的设计水平，减小其引起的船尾振动和辐射噪声是极其重要的[1-4].由于船舶吨位和航速上的需要，相当一部分船舶特别是军船很多采用的是双桨共同工作，但目前国内外关于船体脉动压力计算的文献中基本上只考虑了单个桨螺旋桨的影响 ，因此建立考虑双桨共同作用下船体脉动压力的计算方法具有理论意义和工程使用价值.由于双桨之间转速和相位之间的差别，双桨共同工作时对船体产生作用比单桨要复杂得多、本文提出了空泡螺旋桨诱导的双桨船脉动压力数值预报方法，通过计算比较，探讨了考虑双桨作用与只考虑单桨作用时脉动压力计算结果的差别，并研究了双桨相位差对脉动压力计算结果的影响.

1 空泡预报

要计算空泡螺旋桨诱导的脉动压力，首先需要对螺旋桨非定常空泡进行计算.本文采用基于速度势的低阶面元法计算螺旋桨非定常空泡.对于局部空泡流动，关于扰动速度势的方程为:

式中:P表示控制点，Q 表示负荷点，SWET、SC、SW分别表示桨叶、空泡和尾流的表面.桨叶用双曲四边形面元进行离散，这样螺旋桨表面就形成一系列的弦向条带.

螺旋桨空泡计算的主要困难在于计算时空泡的范围和厚度分布都是未知的.为了便于求解，本文空泡的计算是分别在桨叶的每一弦向条带上迭代求解的，每一弦向条带上的空泡范围和厚度分布通过该条带上的迭代过程求解，在求解该条带时，主叶其他条带及其他桨叶的影响当成已知，并可以通过迭代更新.当该条带上的空泡计算完成后，将计算对象转移到下一条带上，当所有条带上的解都收敛后，展向迭代过程结束[8-11].在每一弦向条带上应用Bernoulli方程，有

定义空泡数

则VC可以表示:

认为VC由两部分组成:切向速度和横向速度，并认为横向速度与切向速度相比可以忽略不计，所以扰动速度vC可以表示成:

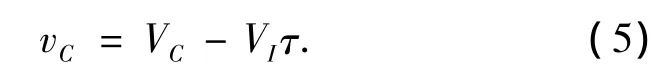
应用式(5)，则空泡表面上的速度势可以表示成:

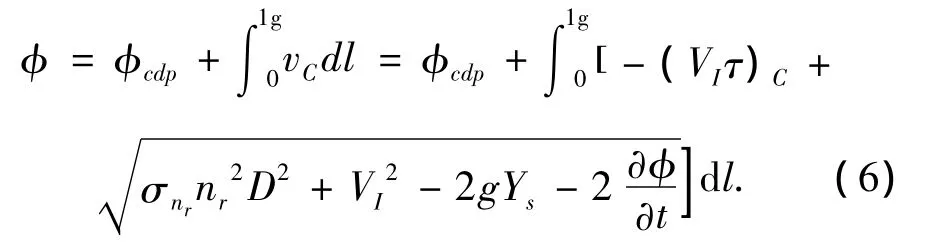
空泡厚度可以通过空泡表面的运动学边界条件求解，并认为空泡厚度的非定常性是小量，可以忽略不计，则空泡厚度的表达式为

2 脉动压力预报

2.1 无限流场中的诱导速度势

在势流理论中，不论用何种方法确定了螺旋桨扰动速度势后，即可按Bernoulli方程确定与之相应的脉动压力.杨建民[1]和熊鹰[2]假定螺旋桨工作于无限自由流场中，对于船体表面和自由表面的影响，通过引入“固壁因子”加以修正.Huse和王国强[3]对船体和自由表面的影响作了研究，提出了估算“固壁因子”和“自由表面因子”的方法.Cox[4]等人在船体表面布置源汇，求解Neumann边值问值，求解过程中必须求出诱导速度的3个分量，计算量大.Breslin[5]在船体表面布置偶极子，将Neumann边值问题转化为Dirichlet边值问题，计算量减少.分别以自由的、刚性的表面模拟自由表面的存在，即将自由表面的影响近似用关于自由表面的船体的正或负映像来表示，从而等同于求解一个绕潜体的流动问题，从而避免了采用“固壁因子”修正引起的误差.Breslin关于船体边界和自由表面的处理方法比较简单且便于编程计算，近年来受到了重视.

叶金铭等[6-7]根据Breslin的思想，在船体表面布置奇点，不同的是，在计算无限流场中螺旋桨诱导的速度势时，是直接通过空泡计算的结果，在桨叶面元和尾流面元布置强度已知的源汇和偶极子，通过格林公式积分得到螺旋桨诱导的速度势，螺旋桨厚度、负荷以及空泡的影响都包含在其中，从而避免了将各部分的脉动压力分开求解;而且船体上的奇点包括源汇和偶极子，求解船体未知偶极子的控制方程中包含了源汇的影响.对空泡问题进行求解后，桨叶面元和尾流面元上的奇点强度已知，可以计算得到螺旋桨对流场中任一点上的诱导速度势:

从式(8)可以看出，只要知道无界流场中任一点的位置(坐标)，就可以通过计算得到螺旋桨对该点的诱导速度势.

2.2 脉动压力

为了便于分析，首先只考虑左桨存在的情况，且船体和螺旋桨处在无限流场中，求解船体表面偶极子强度的控制方程为

如果考虑自由液面的影响，可以采用映像法，给船体和螺旋桨也建立一个映像，建立重叠模型，重叠模型以自由液面为对称面.

如果用高频自由液面条件((2πnZ)2≫g，n为螺旋桨转速，Z为桨叶数)，在自由表面上应该满足条件φ=0，所以映像上的奇点分布始终和原像对应点上的起点强度相等，符号相反(包括船体和螺旋桨).

建立上面的重叠模型后，得到求解船体表面偶极子强度的控制方程为:

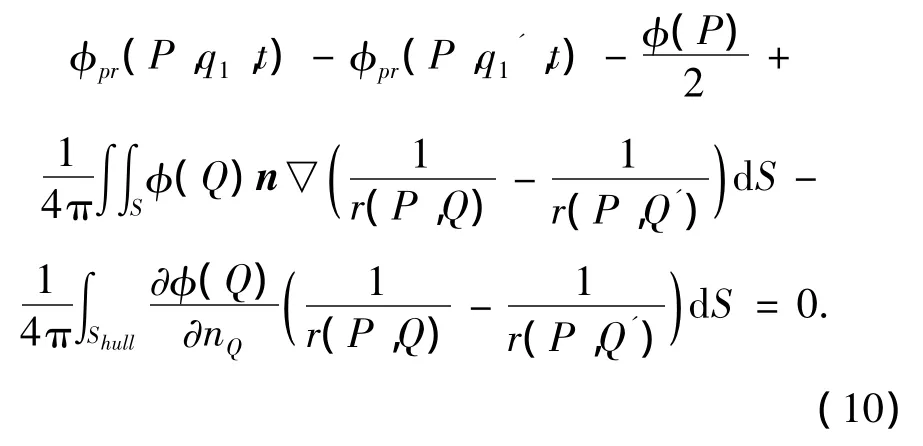
式中:螺旋桨映像的诱导速度势φpr(P，q1'，t)可以通过 φpr(P，q1，t)得到，即

上面的控制方程只考虑了左桨单独存在的情况，若考虑左、右桨同时存在的情况，形成如图1所示的四桨重叠模型.

图1 双桨船重叠模型Fig.1 Double hull model of two-screw ship

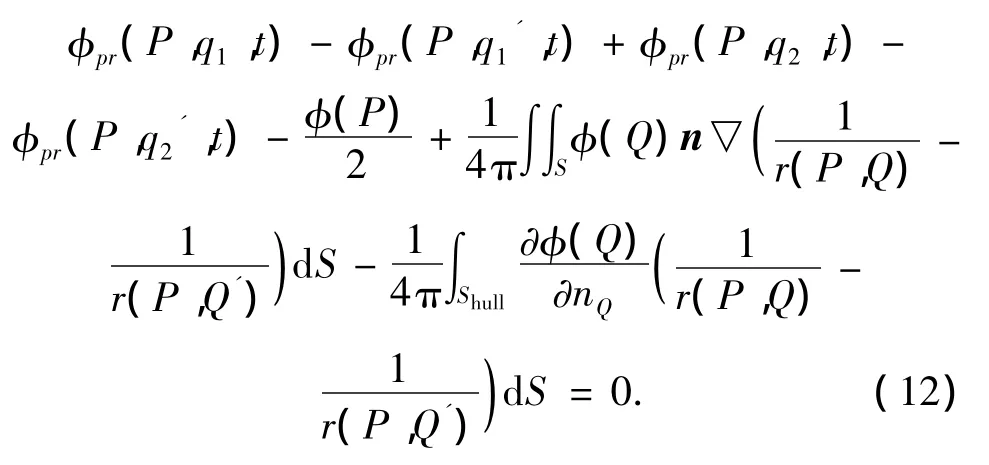
则上面的求解方程变为

如果左桨和右桨旋转角度完全对称，这样右桨q2和它的映像q2'对船体的诱导速度势可以用左桨q1及其映像q1'对船体表面的诱导速度势 φpr(P，q1)、φpr(P，q1')转换得到，即

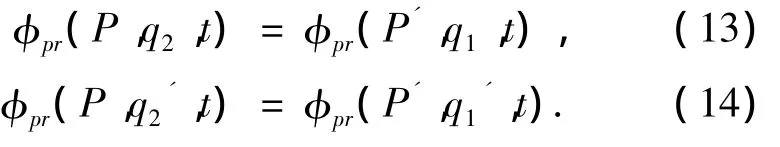
其中，点P'是点P关于船中纵剖面的对称点.

如果左桨和右桨存在的相位差为Δθ，则存在下面的结果:

在脉动压力模型实验中，经常是以平板代替自由液面，在自由表面上应该满足条件，所以映像上的奇点分布始终和原像对应点上的奇点强度相等，符号相同(包括船体和螺旋桨).这时求解双桨船脉动压力采用的控制方程变为

对积分方程进行离散可以求解得到船体偶极子强度分布，然后可求出船体表面的速度分布，用Bernoulli方程就可以求出船体表面的脉动压力.再用Fourier分析就可以得到各阶叶频脉动压力幅值.

2.3 结果及分析

对两艘双桨船H1和H2的脉动压力进行计算，螺旋桨桨模的主要参数见表1.

式中:P为场点，t为时间，pk为第阶叶频脉动压力，Z为桨叶数，εk表示第阶叶频相位角，并将压力幅值无因次化，得到各阶叶频脉动压力系数:

表1 H1和H2主要参数Table 1 The main parameters of H1and H2

在H1的脉动压力模型试验中，对船体上8个点的脉动压力进行了测量，测点布置如图2，其中6#测点位于螺旋桨的正上方;在H2的脉动压力模型试验中，也是对船体上8个点的脉动压力进行了测量，测点布置如图3，其中2#测点位于螺旋桨的正上方.计算工况见表2，轴向伴流分布见图4.

图2 H1脉动压力计算点分布Fig.2 The positions of the measurement points of H1

图3 H2脉动压力计算点分布Fig.3 The positions of the measurement points of H2

表2 H1和 H2计算工况Table2 The work conditions of H1and H2

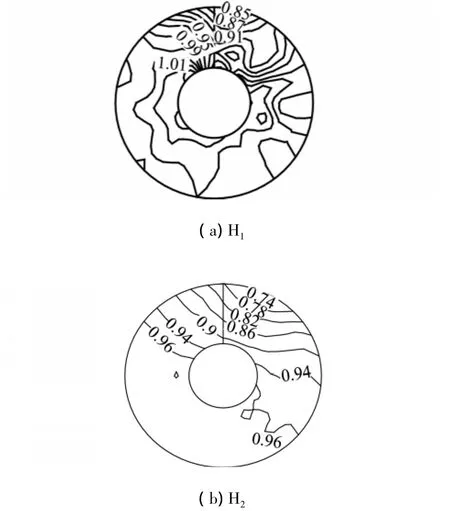
图4 H1and H2伴流分布Fig.4 Wake distribution of H1and H2

首先只考虑左桨对船体诱导的脉动压力.因为在试验中用平板代替自由液面，为了和试验中的边界条件相吻合，用低频自由液面条件的控制方程式(17)但排除右桨的作用进行求解.计算得到的H1和H2左半船体上的一阶叶频脉动压力系数分布云图分别见图5和图6，图中x轴沿着船体纵向，指向船后为正，z轴指向船侧，向左舷为正，原点为船体上螺旋桨正上方的点.从图可以看出，脉动压力幅值位于螺旋桨的右上方，也就是说，脉动压力峰值偏向于高伴流区.

图5 H1船体一阶叶频脉动压力分布Fig.5 The 1st blade frequency pressure fluctuations contour of H1

图6 H2船体一阶叶频脉动压力分布Fig.6 The 1st blade frequency pressure fluctuations contour of H2

各测点脉动压力预报值和试验值的比较见图7和图8.

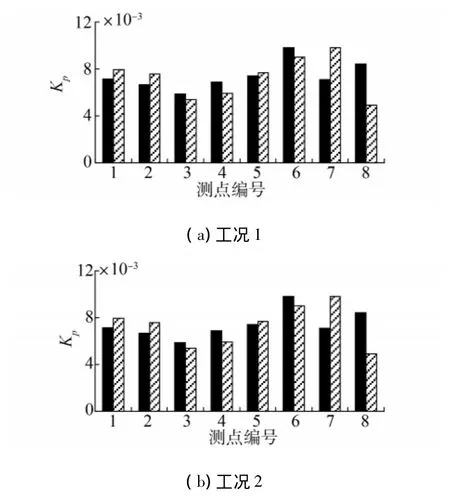
图7 H1各测点一阶叶频脉动压力计算值和试验值比较Fig.7 The 1st blade frequency pressure fluctuations comparison of H1

图8 H2各测点一阶叶频脉动压力计算值和试验值比较Fig.8 The 1st blade frequency pressure fluctuations comparison of H2

图中每个测点上的2个直方图分别表示试验测量值和本文计算值.从比较结果可以看出，大部分测点脉动压力的计算值和试验值吻合得很好.其中，H1中7测点和8测点误差较大可能的原因是这2个测点靠近船体内侧，右桨对这2个测点脉动压力的影响较大，如果计算中不考虑右桨的影响，对于离船中纵剖面较近的点，脉动压力计算的误差必然会比较大.H1中3#测点的误差以及H2中2#测点和7#测点的误差也较大，可能的原因是这些测点附近，脉动压力的梯度很大，这可以从图7和图8看出，导致传感器安装位置的微小误差，也会使测量结果产生相当大的误差.

为了计算双桨共同作用下的脉动压力，并研究双螺旋桨相位差对脉动压力的影响，令螺旋桨间的相位差分别为 0°、12°、24°、36°、48°、60°，计算双桨对船体上各面元上产生的脉动压力，进而进行Fourier分析得到各面元各阶叶频脉动压力.由于各测点不一定正处在面元的中心，根据各测点的坐标进行插值可以得到测点的各阶叶频脉动压力.H1和H2脉动压力计算结果分别见图9和图10

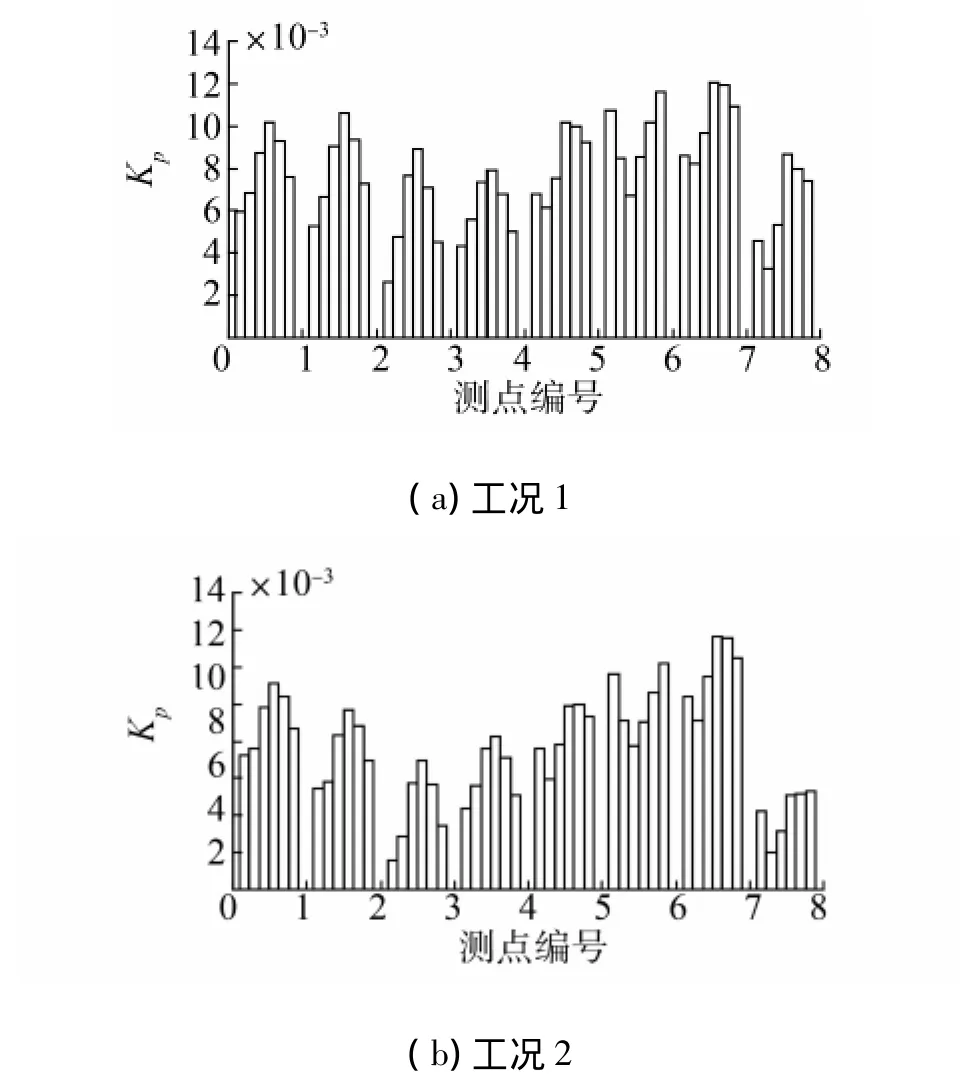
图9 H1不同相位差下的脉动压力计算值结果Fig.9 The pressure fluctuations at each angel-difference of H1

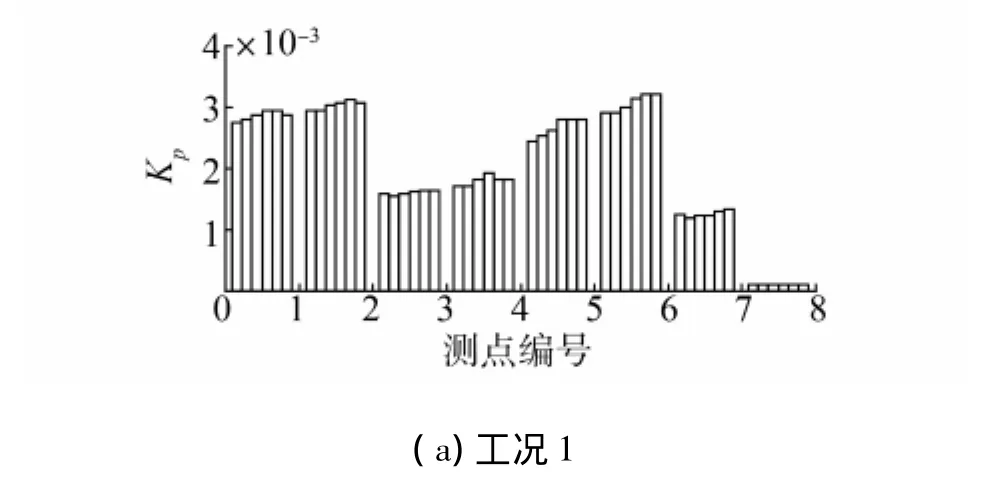
图10 H2不同相位差下的脉动压力计算值结果Fig.10 The pressure fluctuations at each phase-difference of H2

图中每一计算点上的第一个直方图表示只考虑左桨对船体脉动压力影响时的计算值，其他直方图分别对应双桨相位差为 0°、12°、24°、36°、48°、60°的脉动压力系数.从计算结果可以看出，计算螺旋桨对船体的脉动压力时，只考虑单桨和同时考虑双桨的影响得到的计算结果不同，而且双桨的相位差对脉动压力的计算结果有影响，相位差不同得到的计算结果有明显差别，以船体靠近内侧的点最为显著，可能的原因是，船体内侧的点离两只桨的距离都比较近，双桨的作用都比较显著，所以相位差的影响就比较明显.

比较H1和H2的计算结果可以看出，H1船各计算点脉动压力变化的幅度明显比H2船大，可能的原因是，H2船的双桨相对间距大，相位差的影响较小.可见相位差对脉动压力的影响程度和双桨之间的距离有关.双桨的距离较近时，相位差的影响显著，随着双桨距离加大，相位差的影响减小.

3 结束语

本文对双桨船脉动压力进行了计算，计算时考虑了左右螺旋桨之间的相位差对脉动压力计算的影响，结果证明计算双桨船的脉动压力时，只考虑单桨和同时考虑双桨的影响得到的计算结果不同，同时考虑双桨影响时，相位差的影响不能忽略，不同的相位差得到的计算结果有明显差别.

越靠近船体内侧，相位差的影响越大.相位差的影响还同双桨的距离有关系，双桨的距离较近相位差的影响显著，随着双桨距离加大，相位差的影响减小.

在进行脉动压力模型测试和实船试验时，在相同的工况下，前后2次测量分析得到的叶频脉动压力可能有明显差别，上面的结论可以部分解释这种现象.这也提醒试验人员在进行双桨船脉动压力试验时，如果双桨的距离比较近时，在能保证双桨转速完全相同的情况下，还要注意双桨之间的相位差的影响.

[1]杨建民，空泡螺旋桨激振力及船体尾部振动的计算[D].上海:上海交通大学，1987:1-15

[2]熊鹰.空泡螺旋桨诱导的船体表面力的计算[C]//武汉造船工程学会论文集.武汉，中国，1991:73-80.

[3]HUSE E，WANG G Q.Cavitation-induced excitation forces on the hull[J].Trans SNAME，1982，90:85-109.

[4]COX B D，VORUS W S，BRESLIN J P，et al.Recent theoretical and experimental development in the prediction of propeller-induced vibratory forces on nearby boundaries[C]//Proceedings of 12th Symposium on Naval Hydrodynamics.Washington，D C，USA，1978.

[5]BRESLIN J P，HOUTEN R J，KERWIN J E，et al.Theoretical and experimental propeller-induced hull pressures arising from intermittent cavitation，loading and thickness[J].Trans SNAME，1982，90:111-151.

[6]YE Jinming，XIONG Ying.Predicting pressure fluctuations on ship hulls due to intermittently cavitating propellers[J].Journal of Ship Mechanics，2005，9(6):21-29.

[7]叶金铭，熊鹰，韩宝玉.预报脉动压力的几种数值方法[J].哈尔滨工程大学学报，2008，29(12):1266-1271.YE Jinming，XIONG Ying，HAN Baoyu.Several methods for predicting pressure fluctuations[J].Journal of Harbin Engineering University，2008，29(12):1266-1271.

[8]叶金铭，熊鹰.螺旋桨非定常空泡数值预报中的几个问题[J].武汉理工大学学报，2006，30(6):961-964.YE Jinming，XIONG Ying.Numerical and experimental research on pressure fluctuations induced by propeller cavitation[J].Journal of Wuhan University of Technology，2006，30(6):961-964.

[9]叶金铭，熊鹰.螺旋桨空泡数值研究[J].哈尔滨工程大学学报，2006，27(2):172-175.YE Jinming，XIONG Ying.Numerical analysis of propeller cavitation[J].Journal of Harbin Engineering University，2006，27(2):172-175.

[10]XIONG Ying，YE Jinming，WANG Dexun.Prediction of unsteady cavitation of propeller using surface panel method[J].Journal of Hydrodynamics，Ser.B，2005 ，17(1):43-49.

[11]YE Jinming，XIONG Ying.Prediction of podded propeller cavitation using unsteady surface-panel method based on velocity potential[J].Journal of Hydrodynamics，2008，20(6):912-918.

[12]YE Jinming，XIONG Ying，LI Fang.Numerical prediction of blade frequency noise of cavitating propeller[J].Journal of Hydrodynamics，Ser.B，2012，24(3):371-376.