RSA乘法同态的数据库密文检索实现
魏占祯,杨亚涛,陈志伟,2
(1.北京电子科技学院 通信工程系,北京 100070;2.西安电子科技大学 通信工程学院,陕西 西安 710071)
目前,由于部分的网络数据库大量使用明文来保存用户密码,用户的信息隐私保护面临着巨大的风险,尤其在数据库中用户敏感信息的保护与数据泄漏的防止正在越来越受到关注.
相对于单服务器模式的数据库安全[1],在网络环境下,数据库中数据的安全存储以及安全检索目前采用的数据加密与身份认证手段,都只是一次性的将明文信息隐藏化[2],能在一定程度上达到保护隐私数据的目的,但随着用户与网络数据库服务提供商之间交互信息的增多,隐私信息和身份认证信息很容易因被跟踪而导致信息泄露[3].
数据库加密方法可以应用在单机环境和网络环境下,但存在一个共同的问题,即对于所形成的密文数据库无法进行操作,即对于密文数据库,若要对某些字段进行统计、平均、求和等数学运算时,必须先对这些字段进行解密运算,然后对明文进行数学运算,之后再加密.这样首先增大了时空开销;其次,在实际应用中,对于某些重要或敏感数据,无法满足用户对其进行操作但又不能让用户了解其中信息的需要.如果在数据库中存储用同态加密[4]方式加密的数据,就可以实现对密文的检索和计算.
同态密码(homomorphic cryptograph)可认为由Rivest、Adleman等于1978年最早提出的,也称为保密同态(private homomorphic)[5].
Craig Gentry提出的基于理性格的完全同态算法[6-7]运算效率比较低,虽然许多研究者对该算法进行改进[8-9],但是在实际应用中仍存在不少困难.
目前,国内外对密文数据库存储与检索的研究还比较少,至今还没有看到高效可用的同态加密数据库密文检索算法.Yong Zhang等提出一种数据库密文索引策略[10],通过SQL语句翻译器将SQL检索语句转换为对索引的快速匹配.
Yong Zhang还提出一种字符型数据密文的分区索引方法[11].Lianzhong Liu等提出一种基于 Bloom Filter的数据库索引方法[12],根据数据库索引的匹配可将部分不符合检索条件的数据库记录排除.Youssef Gahi等[13]在文献中提出一个利用完全同态加密技术对加密数据执行SQL语句的安全数据库系统,利用Gentry提出的完全同态算法和文献[14]中提供的计算方法,运用普通的同态加密算法实现了对密文数据库的查询、更新、删除等操作,但实现效率非常低.
1 密文检索方案设计
在网络存储环境中,为了保护用户的数据安全和防止隐私信息泄露,用户与数据存储服务提供商之间多次交互时可以利用密文进行操作,这些数据是以密文的形式存在数据库中.常规的思路是,把明文数据记录加密为密文之后,上传到网络存储服务器,需要的时候执行对数据库的查询操作并获得数据记录.但这样的思路在数据记录的发送阶段、查询阶段以及接收与解密阶段涉及到多个加/解密操作,并且因为在查询阶段,用户的数据被完全打开,处于明文状态,也就无法保证用户隐私数据在查询阶段的私密性.所以,采取同态加密的思路来实施对网络环境中的数据进行同态加密存储和安全获取,以便保证在适当增加计算开销的情况下,确保用户数据的私密性.
1.1 RSA密码体制的同态性分析
使用RSA密码体制在完成加解密运算时,首先选取2 个大素数 p、q,计算 n=pq,φ(n)=(p-1)(q-1);随机选取一个整数e要求满足:1<e<φ(n)-1,(e,φ(n))=1,求出 d,0 < d < φ(n),ed=1 modφ(n).此时,公钥为(e,n),私钥 d;加密过程:c=memodn,解密过程:m=cdmodn.
对于明文m1、m2,采用RSA体制加密后,可以得到所以RSA公钥密码体制满足乘法同态特性.
举例:假定RSA的公钥、私钥分别为(5 437,189 781)与(49 269),2个明文信息分别为m1=56 947,m2=64 413,根据RSA的乘法同态特性,可以得到:

1.2 数据库中密文检索协议构造
假定数据库中的数据记录以密文存放,采用的加密算法为RSA,数据拥有者O(即提供者)和数据获取者D是同一实体,即数据拥有者发送自己的密文数据C到数据库服务器,自己需要时,再获取这些数据.假设密文C对应的明文是M,选用的具有乘法同态特性的公钥密钥体制可以为目前通用的RSA.
1)向数据库服务器发送数据
O发送数据M时,可以对M用自己的公钥进行加密,形成密文C,把C发送到数据库服务器;同时,选定 t个 M 对应的关键词 kw1,kw2,…,kwt,t的选取以能够恰当表达M的属性为原则,同时,要考虑到引入的计算量,实际中可以t=3;对t个关键词分别用t个公钥进行加密,得到t个密文关键词ckw1,ckw2,…,ckwt;然后获得如下乘积:Ckw=ckw1ckw2…Ckwt,把Ckw也一并发送到数据库中.详细说明如下:
例如,3个关键词 kw1,kw2,kw3分别用3个公钥进行加密:

式中:n是2个大素数p,q的乘积,n=pq,φ(n)=(p-1)(q-1);Ri是随机选取的素数,满足1<Ri<φ(n)-1,(Ri,φ(n))=1;所以,此时可以认为,数据拥有者自己采用的RSA加密算法的密钥(与RSA算法中的公钥不同,在这里称他们为密钥)为Ki=(Ri,n)(i=1,2,…,k);
其次,数据拥有者把t个密文关键词ckw1,ckw2,…,ckwt的乘积Ckw=ckw1ckw2…ckwt也一并发送到数据库.
2)从数据库服务器获取数据阶段.
当D(也就是O),想从数据库服务器获取想要的记录时,用明文输入关键词KW,可以对kw1,kw2,kw3进行联合加密,根据加密算法的乘法同态特性:E(kw1)E(kw2)…E(kwt)=E(kw1kw2…kwt),
即ckw1ckw2…ckwt=Ckw;服务器在数据库中查询与KW匹配的数据记录,如果匹配的关键词存在,就提取该记录.把C以密文形式下载到D,所以当D得到这些密文分片后,就可以得到C.详细如下:当数据获取者(也就是数据拥有者)取定3个检索的关键字kw1,kw2,kw3后,并根据数据库中的 R(R=R1R2R3),就可以对 kw1,kw2,kw3进行联合加密:
EPK(kw1kw2kw3)=C≡(kw1kw2kw3)Rmodn,R是k个随机素数的乘积R=R1R2…Rk,所以,此时数据获取者所采用的RSA加密算法的公钥为PK=(R,n),这也是数据拥有者向外公布的RSA加密算法的公钥.
3)然后利用自己的私钥即可解密得到明文M.
需要说明的是,上述方案中数据拥有者仅仅上传了Ckw和R到数据库服务器中,为数据获取者提供一次性多个(例如3个)关键词的快速检索;也可以另外把3个关键词的密文及其公钥(kw1,R1),(kw2,R2)(kw3,R3)上传到服务器,以便供数据获取者提供单个关键词的检索.
通过上述过程,数据库服务器上存放的是数据的密文C和Ckw,也就是说,数据的私密性和安全性得到保障;方案利用RSA的乘法同态特性,提供了t个关键词的一次性快速检索,提高了检索效率.
1.3 带有隐私保护的同态密钥协商
现在假定,数据拥有者O(即提供者)的RSA公私钥对为(PK0,SK0),数据获取者D的RSA公私钥对为(PKD,SKD),数据库服务器S的RSA公私钥对为(PKs,SKs),则可以设计如下的同态密钥协商协议:
1)数据拥有者O(即提供者)向服务器S发出数据上传请求EPKS(IDO)=(IDO)PKS,IDO是数据拥有者O的身份标识(可以是IP或MAC地址,或其他序列号).
2)服务器S生成一个随机数RS并用O的公钥加密后返回给 O,即 EPKO(Rs)=(IDO+1‖ID‖SRS)PKO,IDS是服务器S的身份标识(可以是IP或MAC地址,或其他序列号).
3)0用自己的私钥解密数据EPKO(RS)=(ID0+1‖IDS‖RS)PKO,可以得到 RS,同时可以验证服务器S的身份是否合法.
4)O生成一个随机数R0,然后可以得到用于数据上传的数据加密密钥K=RORS.
5)O用生成的数据加密密钥K,采用对称加密算法(例如AES)加密要上传的数据Data,即EK(Data).
至此,数据的加密上传已经完成,由于数据服务器无法生成数据加密密钥K=RORS,即其无法解密由用户上传的数据,用户数据的私密性得到了保障.
当数据获取者D检索到合适的数据,打算下载并使用EK(Data)时,可以采取如下思路:
①数据获取者D分别向数据拥有者O和数据库服务器S发出请求,他们分别返回用数据获取者D的公钥加密的随机数,即
②利用RSA加密体制的乘法同态特性,数据获取者D做如下运算,然后解密,就可以得到K=RORS.
③用密钥K,就可以解密得到明文数据Data.
1.4 协议的安全性证明
BAN逻辑是由Burrows等提出的一种基于信仰的逻辑[15],下面基于BAN逻辑对提出的协议进行安全性分析.本文提出的协议主要目的是在三方之间建立起逻辑密钥,该协议的初始假设为:
三方交互协议的步骤可以形式化为:
4)S◁{#Data}EK
见规则,D可以构造K=RORS
由新鲜规则、看见规则和4),可以得到:
与S、D之间的会话公钥是K”
由上述步骤看出,提出的协议是安全的.流程实现了安全的密钥协商.协议中,随机数的传输都是用对方的公钥进行加密,只有合法接受者的私钥才能解密数据,保障了随机数和数据的安全性,实现了接收方的不可抵赖性.另外,步骤1)~3)可以看作是一个双向认证流程,有效防止了中间人攻击和重放攻击.
2 方案分析与密钥获取性能测试
对所提出的方案进行如下分析:
1)解决了联合授权问题,特别适宜于有三方关联需求的商业应用场景.方案中,数据提供者提供自己的数据,数据服务器提供数据展示的平台,数据获取者期望获得想要的数据服务.通过该方案,数据获取者必须在获得数据提供者和服务器双方共同授权的情况下(同时获得RO和RS),才能解密得到数据Data,即:1)数据获取者可以向数据提供者和服务器双方支付相关的费用或发出请求授权,以便来获得想要的数据资源和服务;2)也有利于数据提供者和服务器对所拥有的相关资源进行有效管理和控制.
2)保护了数据隐私.由于数据服务器无法生成数据加密密钥K=RORS,即其无法解密由用户上传的数据,用户数据的私密性得到了保障.
3)减少了计算开销.在第7)步,数据获取者D只需1次乘法操作和1次解密操作,即可得到K=RORS;即采用方法1(RSA乘法同态机制)来获取会话密钥:

相反,如果不利用RSA的乘法同态特性,数据获取者D只能方法2来获取会话密钥:

需要做2次解密操作和1次乘法操作,即2次解密分别得到RO和RS,再用乘法得到K=RORS.由于RSA的解密操作比较耗时,所以提出的思路提升了解密密钥的获取效率.为了验证这2种情况下获取密钥的性能,实施了实验仿真并进行了效能测试.实验采用 Openssl密码算法库中的 256、512、1 024、2 048 bit RSA生成的密钥,采用无密文填充的加密方案,实现了基于RSA乘法同态特性的密钥获取效率对比.服务器环境为:AMD Athlon(TM)II X2 250 Processor双核CPU,DDR3 1 333 MHz 2G 内存,Windows XP SP3,Visual Studio 2010 Win32 Console Application,其中模拟测试核心部分伪码如下:


首先,采用512 bit的随机数RO和512 bit的随机数RS,在RSA模数n的不同取值(n=256,512,768,1 024,2 048,4 096)情况下,分别采用乘法同态和不采用乘法同态的2种RSA算法,对比测试了2种密钥获取方式,得到了2种机制情况下的所获得密钥K的生成时间对比结果,如图1所示.

图1 RSA算法获取密钥的2种方案效率对比Fig.1 The performance comparison between the two encryption key generators based on RSA
由图1可知,利用乘法同态所获取密钥的时间基本上是不采用乘法同态的一半,即密钥获取效率几乎提升了50%.
其次,改变随机数RO和随机数RS的位数,让它们分别取值为 64、128、256、512 bit,选取 RSA 的模数n=1 024 bit,分别采用乘法同态和不采用乘法同态的RSA算法,测试了2种密钥获取方式,得到了2种机制情况下所获取密钥K的计算耗时对比结果,如图2所示.
由图2可知,利用乘法同态所获取密钥的时间基本上也是不采用乘法同态的一半,即密钥获取效率也提升了近50%.同时,从图2平稳的折线中可以明显看出获得不同位数的解密密钥K所消耗的时间在 2种方法下变换不大.也就是说,获取1 024 bit的解密密钥与获取较短长度的解密密钥耗时几乎相当.
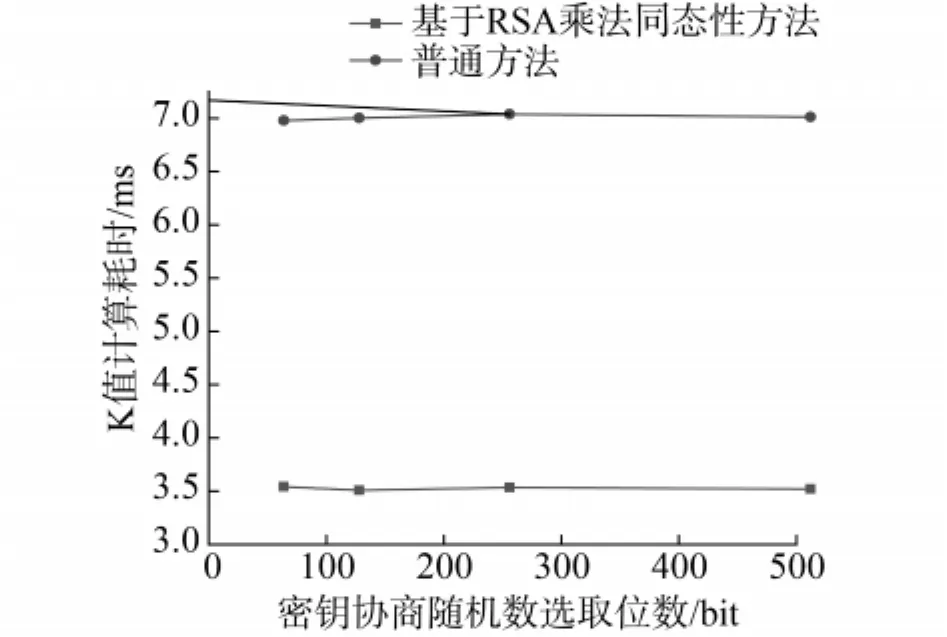
图2 K值进行密钥获取的2种方案效率对比Fig.2 Performance comparison between the two encryption key generators based on different size of Keys
3 结束语
本文以网络环境下数据存储的安全问题综合分析为切入点,提出了一种新的带有隐私保护的同态密钥协商方案,保障了用户在数据记录的发送阶段、查询阶段以及接收阶段用户数据的私密性,并对所设计的协议进行了安全性证明;对密钥获取的性能进行了对比测试,仿真表明,利用RSA的乘法同态性质所获取密钥的时间基本上相当于不采用乘法同态的一半,即数据获取者获取解密密钥的效率提升了近50%.本方案为网络数据库的数据隐私与安全提供了一条有效解决思路.研究基于ECC公钥密码体制同态特性的密文存储与检索算法将是本文下一步的研究方向.
[1]CASTAGNOS G,CHEVALLIER M B.Towards a DL-based additively homomorphic encryption scheme[C]//Proceedings of 2007 Information Security Conference(ISC 2007).Berlin:Springer-Verlag,2007:362-375.
[2]陈康,郑纬民.云计算:系统实例与研究现状[J].软件学报,2009(5):1337-1348
CHEN Kang,ZHENG Weimin.Cloud computing:system instances and current research[J].Journal of Software,2009(5):1337-1348.
[3]SADEGHI A R,SCHNEIDER T,WINANDY M.Tokenbased cloud computing secure outsourcing of data and arbitrary computations with lower latency[C]//Proceedings of 3rd International Conference on Trust and Trustworthy Computing(TRUST 2010).Berlin,Germany,2010:417-429.
[4]GENTRY C.A fully homomorphic encryption scheme[D].Stanford:Stanford University,2009:25-88.
[5]RIVEST R L,ADLEMAN L,DERTOUZOS M L.On data banks and privacy homomorphism [M].New York:Academic Press,1978:169-179.
[6]GENTRY C.Fully homomorphic encryption using ideal lattices[C]//Proceedings of 41st ACM Symposium on Theory of Computing(STOC 09).New York,USA,2009:169-178.
[7]GTOTH J.A verifiable secret shuffle of homomorphic encryptions[C]//Proceedings of 30th International Cryptology Conference(Crypto 2010).Berlin,Germany,2010:546-579.
[8]SMART N P,VRECAUTEREN F.Fully homomorphic encryption with relatively small key and ciphertext sizes[C]//Proceedings of 13th International Conference on Practice and Theory in Public Key Cryptography.Berlin,Germany,2010:420-443.
[9]DIJK M,GENTRY C,HALEVI S,et al.Fully homomorphic encryption over the integers[C]//Proceedings of 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques(EUROCRYPT 2010).Berlin,Germany ,2010:24-43.
[10]ZHANG Yong,LI Weixin,NIU Xiamu.A secure cipher Index over encrypted character data in database[C]//Proceedings of 2008 International Conference on Machine Learning and Cybernetics.Kunming,China,2008:1111-1116.
[11]ZHANG Yong,LI Weixin,NIU Xiamu.A method of bucket index over encrypted character data in Database[C]//Proceedings of 3rd Intelligent Information Hiding and Multimedia Signal Processing(IIHMSP 2007).Piscataway,USA,2007:186-189.
[12]LIU Lianzhong,GAI Jingfen.Bloom filter based index for query over encrypted character strings in database[C]//Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering.Piscataway,USA,2009:303-307.
[13]GAHI Y,GUENNOUN M,KHALIL E K .A secure database system using homomorphic encryption schemes[C]//Proceedings of the 3rd International Conference on Advances in Databases,Knowledge,and Data Applications(DBKDA 2011).st.Maarten,The Netherlands Antilles,2011:54-58.
[14]SHOR P.Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J].SIAM Journal on Computing,1997,26(5):1484-1509.
[15]BURROWS M,ABADI M,NEEDHAM R.A logic of authentication[J].ACM Transactions on Computer Systems,1990,8(1):18-36.

