基于改进蚁群与动态窗口法的AGV动态路径规划

杨 周，刘海滨

北京工业大学 材料与制造学部，北京 100124

路径规划是自动导引车（automatic guided vehicle，AGV）研究领域的一个重要课题，其目的是在有障碍物约束的环境下，根据已知的起点与终点，以最短路径、最短时间等为目标寻找一条最优或接近最优的安全、无障碍路径[1-2]。根据应用场景的不同，可将路径规划算法分为全局静态路径规划算法和局部动态路径规划算法。全局静态路径规划算法主要应用于全局信息已知的静态环境，常用的算法有Dijkstra算法[3]、A*算法[4]、蚁群算法[5]等；局部动态路径规划算法主要应用于全局信息未知或部分已知的动态环境，常用的算法有动态窗口法[6]、强化学习[7]等。

蚁群算法因具有良好的搜索能力、正反馈特性、并行计算、易与其他算法融合等特性，在全局静态路径规划中得到大量应用。但传统蚁群算法也存在搜索时间长、易陷于局部最优、前期盲目搜索导致收敛性差等缺陷。葛志远等[8]针对传统蚁群算法搜索效率低，耗时长等问题，通过改进启发函数确定搜索方向并利用优胜劣汰机制更新全局信息素，保证算法多样性的同时提高算法收敛速度；王晓燕等[9]针对传统蚁群算法各节点初始信息素均匀分布导致算法初期搜索范围大，收敛性差等问题，提出初始信息素不均衡分配策略，降低了初期搜索盲目性，提高了算法搜索效率。

动态窗口法是常用的局部动态路径规划算法，具有很好的躲避动态障碍物能力，可以实时在线路径规划，且路径较为平滑，符合AGV运动特征。但由于缺少全局信息的指导，规划路径质量较差，且经常无法到达目标点。殷绍伟等[10]利用改进的A*算法改进蚁群算法，然后融合滚动窗口法进行局部实时路径规划，最后使用贝塞尔曲线对路径进行平滑度处理，使路径更加接近AGV实际运动特征；槐创锋等[11]将传统A*算法的3×3搜索领域扩展到7×7，解决了传统A*算法折点多，路径不平滑的问题，然后根据全局最优路径设计动态窗口评价函数，实现了机器人在复杂环境下的实时动态路径规划。

由上述文献可知：全局静态路径规划算法可以有效利用全局信息规划出全局最优路径，但无法躲避动态障碍物；局部动态路径规划算法可以实时在线规划路径，有效躲避动态障碍物，但由于缺少全局信息，易陷入局部最优解，经常出现无法到达目标点的现象。针对这两类算法的缺陷，许多学者将两类算法融合，并在实时动态路径规划方面取得了较好的效果。为在动态环境中实时规划全局最优路径，本文参考融合思想提出了一种结合改进蚁群算法和动态窗口法的全局动态路径规划算法。首先，对蚁群算法提出改进：初始信息素不均匀、双向分布，为蚁群算法双向搜索提供大体方向；引入放大系数A增大相邻栅格启发信息差异，增大蚂蚁选择更优节点的概率；更新信息素选择最优路径时考虑转弯次数的影响，得到更平滑的路径，提升AGV运行效率。然后，设计新的动态窗口法距离评价子函数并动态设置AGV初始航向角。最后，提取改进蚁群算法规划的全局最优路径上的转折点作为改进动态窗口法的子目标点，引导动态窗口法沿着全局最优路径方向进行实时动态路径规划，最终实现有效躲避动态障碍物的同时规划全局最优路径。

1 蚁群算法及改进

1.1 蚁群算法工作原理

蚁群算法是一种来源于自然界的智能随机搜索算法，有很强发现较优解的能力[12]。其工作原理为蚂蚁在觅食过程中通过释放信息素进行群体间信息传递，信息素浓度与路径长度成反比，浓度越高表示路径越短，该路径被其他蚂蚁选择的概率就越高，通过这种正反馈机制能够很快搜索出到达目标位置的无碰撞最优路径。

1.2 蚁群算法的改进

1.2.1 初始信息素不均匀、双向分布

传统蚁群算法初始信息素采用均匀分布的方法，简单易行，但各栅格信息素浓度相同导致算法初期存在盲目搜索，收敛性差等问题[13]。由于双向搜索策略能大大提高算法全局搜索能力、加快前期搜索效率、增大前期有效解，因此本文在基于双向搜索策略下提出初始信息素不均匀、双向分布，为蚁群双向搜索提供大体方向，避免算法初期盲目搜索、收敛性差等问题，并满足任意起点与终点的应用场景。

假设AGV的起点坐标为( xS,yS)，终点坐标为( xE,yE)，则过起点与终点的直线可以用方程L表示：

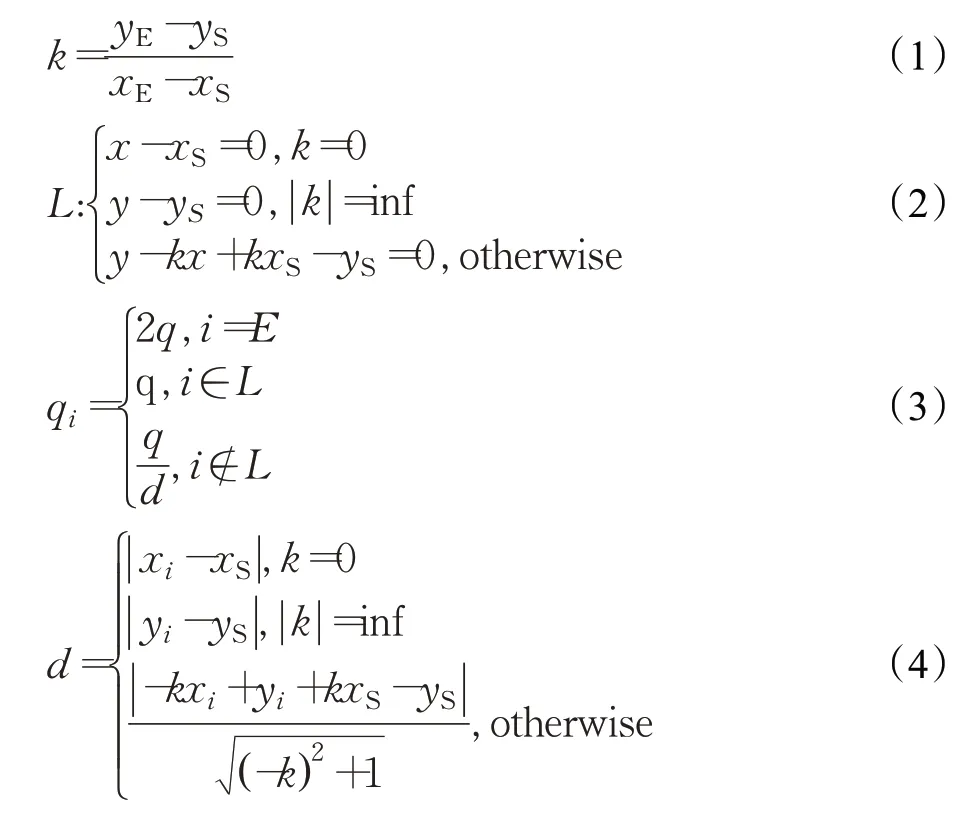
式中，k为连接起点与终点的直线斜率；q为初始信息素均匀分布时的初始值；i为栅格点数；qi为改进后各栅格信息素初始值，d为节点i到方程L的距离。

1.2.2 改进启发信息函数

传统蚁群算法的启发信息函数ηij与栅格i和栅格j之间的距离成反比，但相邻栅格之间的距离差异很小，对路径搜索的引导作用不大。目前，对有效的改进是将蚂蚁下一可选栅格到终点的距离与当前栅格到下一可选栅格的距离的加权和倒数作为启发信息函数[14]。该方法虽然考虑当前栅格转移到下一栅格所付出的代价，但相邻栅格距离差异较小，对整体的启发信息影响也不大。为此，本文引入放大系数A来增大相邻栅格的启发信息差异，从而增大蚂蚁选择更短节点的概率。

式中，ηij为启发信息函数，表示蚂蚁从节点i转移到节点j的期望程度；dij为节点i到下一节点j的欧氏距离；djE为下一节点j到目标节点E的欧式距离；A为放大系数；μ为常数。

1.2.3 改进信息素更新规则

传统蚁群算法采用全局信息素更新方式，只有最短路径上信息素被更新，虽然可以很好地利用最优解信息，但蚁群会过早集中在同一条路径上，降低算法的全局搜索能力，易陷入局部最优解。另外，在更新最短路径上的信息素时，很少有人考虑到最短路径可能并非只有一条，大多只更新其中一条最短路径上信息素，可能会丢失最优解（本文定义的最优解为路径长度最短，转弯次数最少的路径）。针对上述问题，本文提出所有到达终点的路径都进行信息素更新，并找到所有的最短路径，然后在额外奖励最优路径时首次引入转弯次数影响因素（转弯次数的增加会大大降低AGV运行时的工作效率，过于频繁地转向还会加速AGV的损耗，缩短使用寿命），选择转弯次数最少的最短路径作为最优路径更新信息素，从而得到平滑度更高，更符合AGV运行特征的路径。改进后的信息素更新公式为：

式中，ρ为信息素挥发系数，0＜ρ≤1；τij表示t时刻信息素；Δτij为信息素增量，初始时刻Δτij=0；Q为信息素总量；Δτbestij为最优路径上的信息素增量；Lm为到达终点的路径长度；Lbest为最优路径长度。

2 动态窗口法及改进

2.1 动态窗口法基本原理

动态窗口法[15]是在充分考虑到AGV自身机械特性限制以及环境对速度的约束下，在速度二维空间中采样多组速度对（线速度、角速度），在一定时间间隔内同时模拟AGV在这些速度对下的轨迹。获取多组可行模拟轨迹后，根据设计的评价函数，AGV以最优模拟轨迹所对应的速度对，完成局部路径规划。

2.1.1 速度组采样

在速度空间中存在无穷多组速度对(v,ω)，根据AGV自身限制及环境因素，对采样速度范围进行约束：

（1）速度约束

设AGV初始状态下的速度为Vs，则：

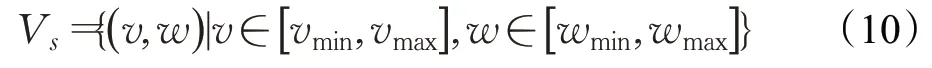
式中，v、w分别表示速度和角速度；vmin、vmax和wmin、wmax分别表示速度和加速度最小值与最大值。

（2）最大加速度约束

由于电机力矩有限，存在最大加速度限制，因此使得AGV轨迹的前向模拟周期内，存在一个动态窗口vd，该窗口的速度集合是AGV在下一个时间间隔内实际能够达到的速度，则：

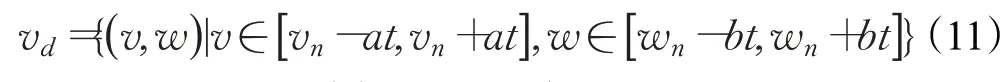
式中，vn、wn分别表示AGV当前状态下的速度与角速度；a、b分别表示AGV的加速度与角加速度。

（3）制动距离约束

为保证AGV的运行安全，在最大减速度下，当前速度应能在撞到障碍物前减速为0，即：

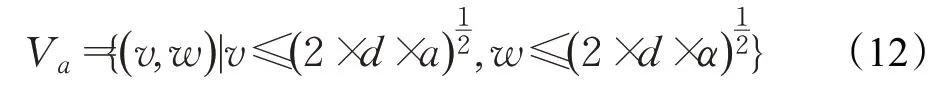
式中，d为速度(v,w)对应轨迹终点到障碍物最近的距离。

2.1.2 设计评价函数

动态窗口法评价函数设计准则是AGV尽量避开障碍物，朝向目标快速前进。设计的评价函数为：

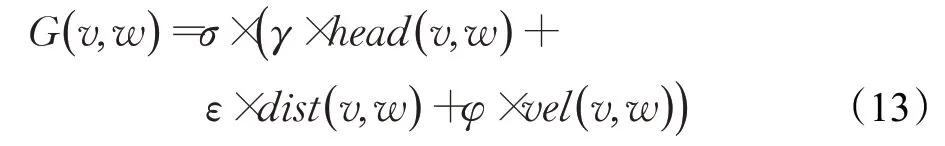
式中，head( v,w)为方向角评价子函数，表示在当前速度下，模拟轨迹终点方向与目标点之间的方向角偏差；dist( v,w)为距离评价子函数，表示在当前速度下，模拟轨迹终点到障碍物最近的距离；vel( v,w)为当前速度大小评价子函数；σ为平滑函数；γ、ε、φ为各评价子函数加权系数。

2.2 改进动态窗口法

2.2.1 改进距离评价子函数dist( v,w)

传统距离评价子函数dist(v,w)，并未考虑模拟轨迹其余点到障碍物的距离，这可能会出现模拟轨迹终点绕开了移动障碍物，但轨迹上的其余点与移动障碍物发生了碰撞的情况，如图1所示。针对这种情况，本文提出了改进的距离评价子函数，以模拟轨迹上所有点到障碍物的最小距离为评价距离，di st越大，表示AGV离障碍物越远。

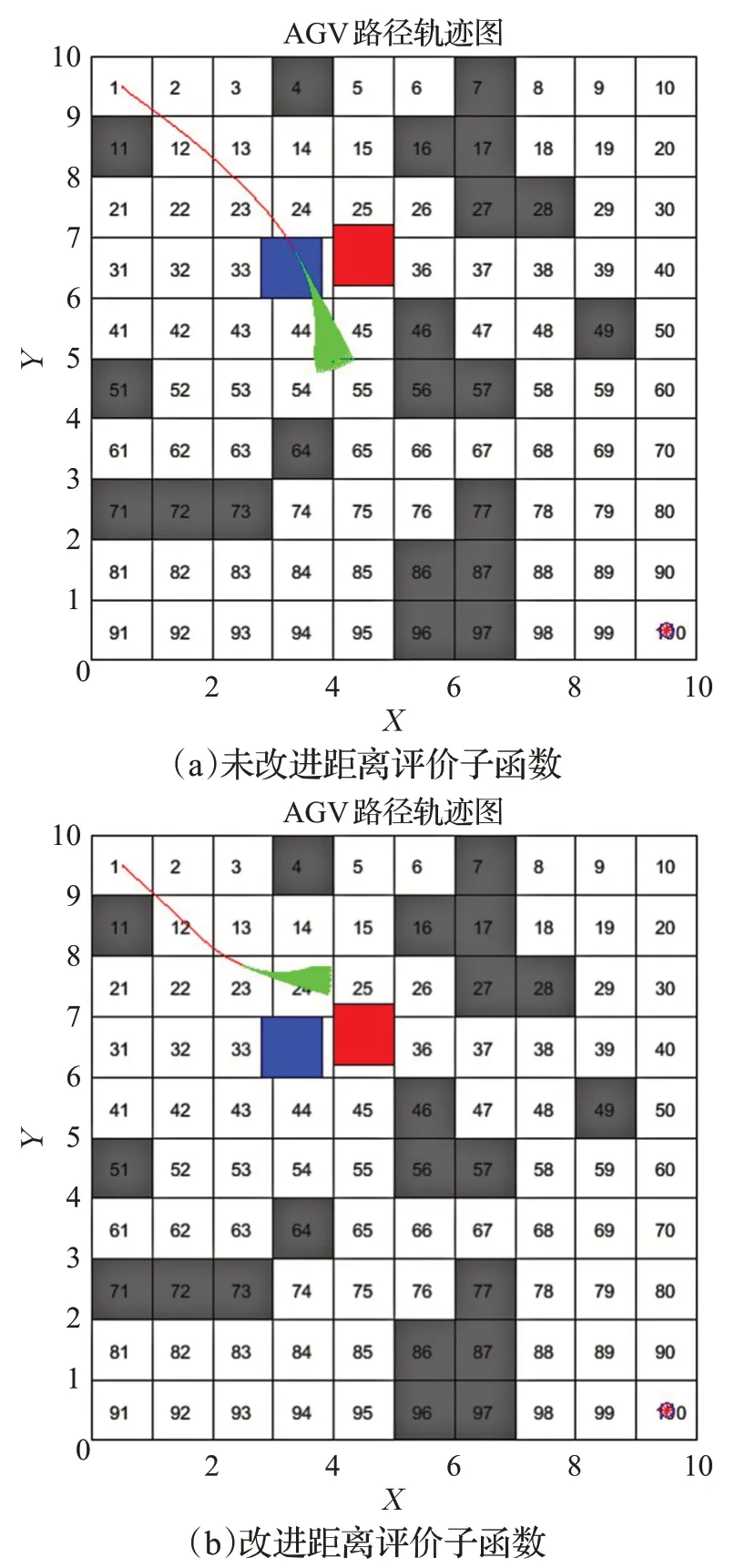
图1 距离评价子函数的影响Fig.1 Influence of distance evaluation sub-function

2.2.2 动态设定AGV初始状态航向角

AGV初始航向角是随机设定的固定角，当与目标点角度偏差较大时，会出现初期搜索路线绕行的现象，增加AGV运行路径的冗余，如图2所示。因此，本文提出了以起点与第一个子目标点的连线与水平方向的夹角来动态设定AGV初始航向角，明确搜索路径的前进方向，避免绕行。

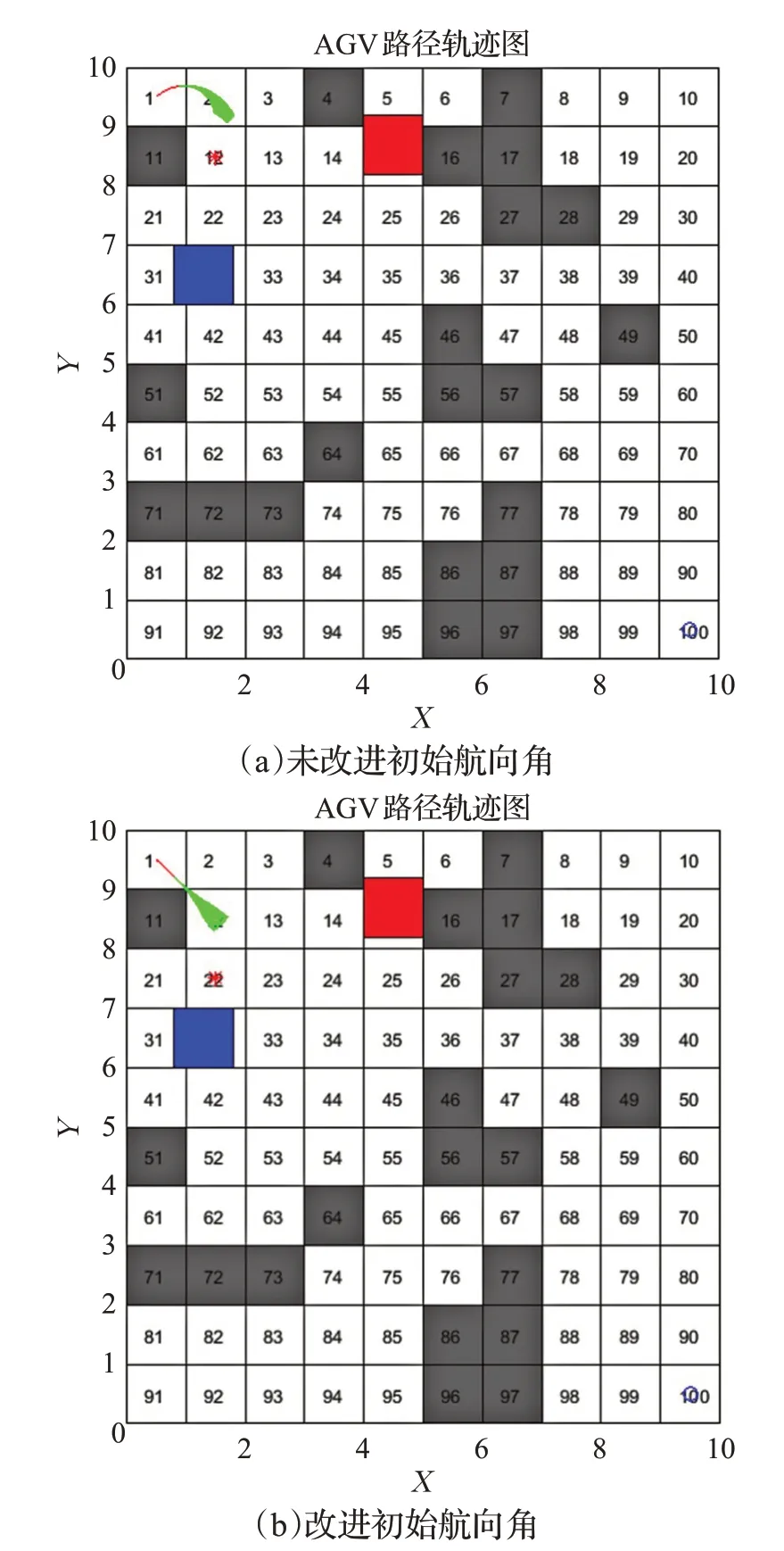
图2 初始航向角的影响Fig.2 Influence of initial heading angle

设起点坐标为(XS,YS)，第一个子目标点的坐标为(X1,Y1)，则AGV的初始航向角φ为：

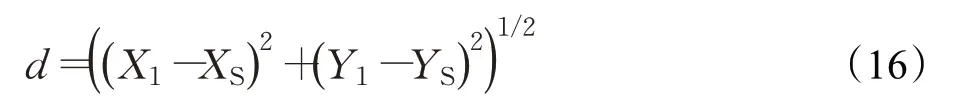
式中，c为初始航向角的正弦值；d为起点与第一个子目标点的欧式距离。

2.3 全局动态路径规划算法

动态窗口法根据AGV检测到的局部环境信息，实时动态规划路径，具有良好的避障能力，但由于无法有效利用全局环境信息，存在易陷入局部最优、无法到达目标点等致命问题。因此，本文提出利用改进蚁群算法进行全局静态路径规划，然后将规划的最优路径上各转折点依次作为改进动态窗口法的子目标点，终点为总目标点，分步指引动态窗口法沿全局最优路径方向进行实时动态路径规划，以保证动态规划路径的全局最优性。若在行程后期出现目标位置转移的情况，可以根据目标点转移状态分为两种情况：（1）若目标点一直移动，则可以利用改进的动态窗口法动态追踪移动目标点，但路径质量可能较差；（2）若目标点转移后静止不动，则可以将当前位置设为起点，转移后的目标位置设为终点，重新调用全局动态路径规划算法进行实时动态路径规划。这里仅简单讨论两种目标转移情况的解决方法，在下文实验中并不考虑目标转移的情况，因此全局动态路径规划算法的具体流程如图3所示。

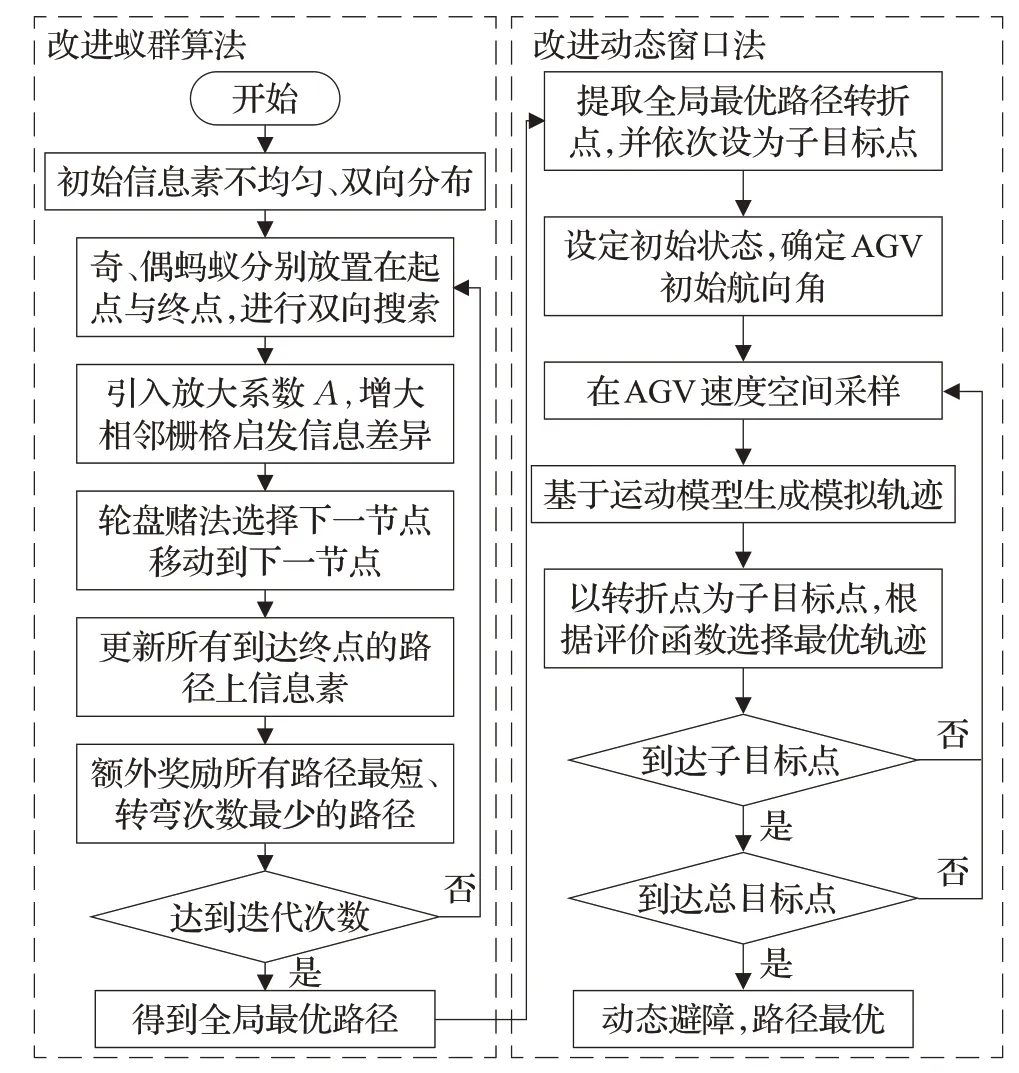
图3 全局动态路径规划算法流程图Fig.3 Flow chart of global dynamic path planning algorithm

3 仿真实验

3.1 基于改进蚁群算法的全局静态路径规划

为了验证改进蚁群算法的可行性和有效性，本文利用编码简单、易于实现的栅格地图法建立模拟环境[10]，在不同模拟环境下，通过Matlab进行传统蚁群算法和本文改进蚁群算法的仿真实验对比。相关实验数据如下：迭代次数K=100，蚂蚁数量M=50，信息素启发因子α=1，期望启发因子β=8，信息素挥发系数ρ=0.4，信息素增量Q=10。

（1）仿真实验环境一（图4～图6）

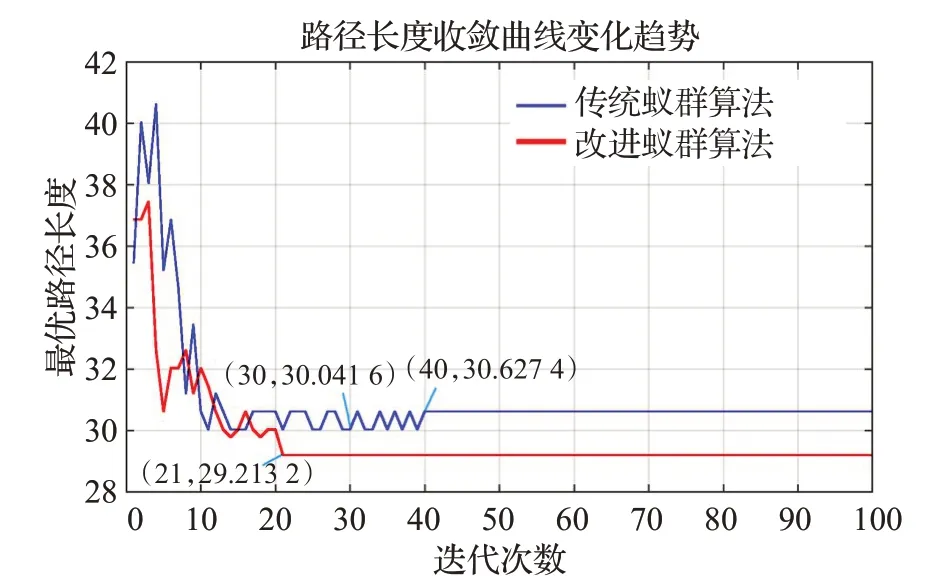
图4 传统与改进蚁群算法的路径长度收敛对比（实验1）Fig.4 Comparison of path length convergence between traditional and improved ant colony algorithms（E1）

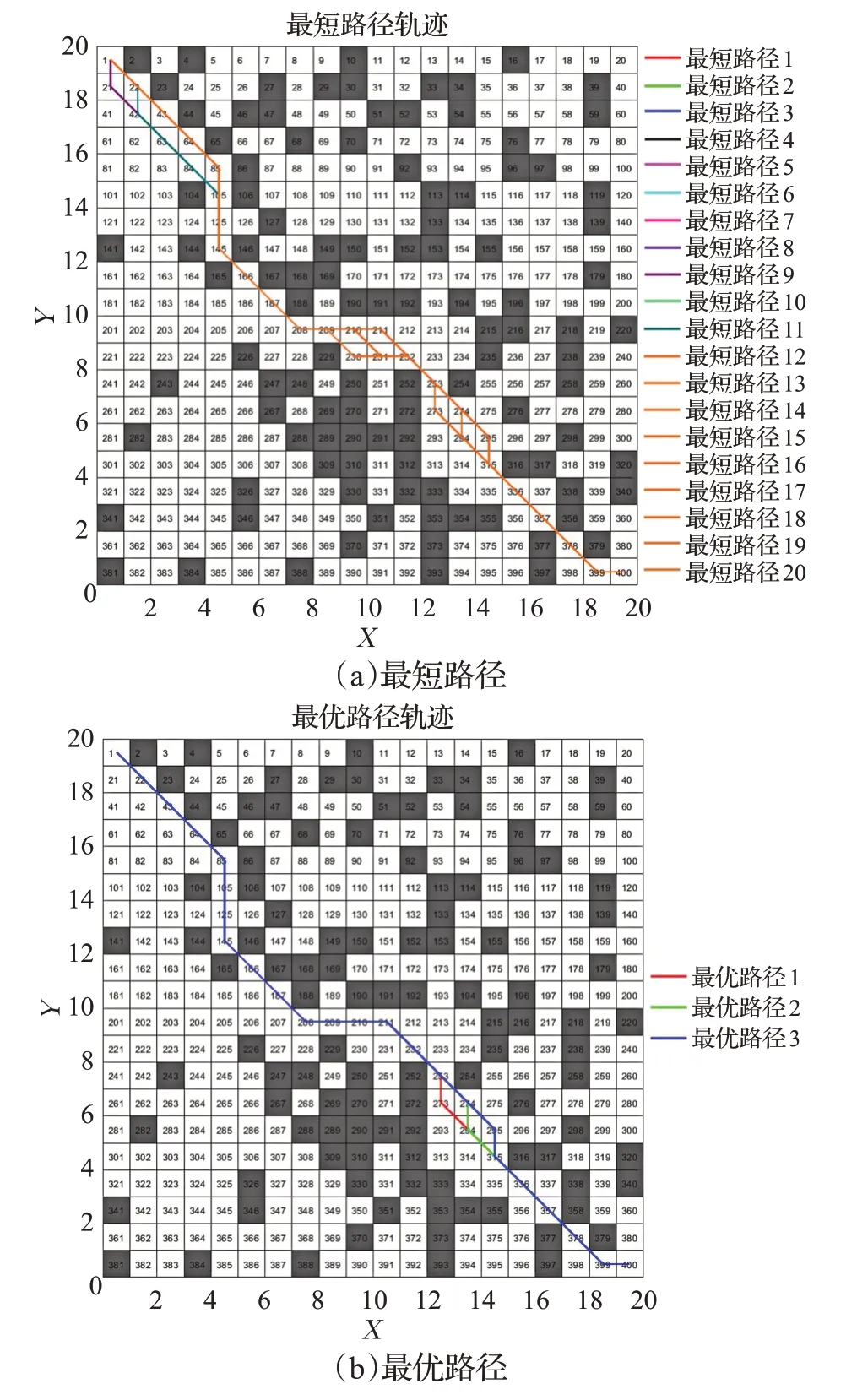
图6 改进蚁群算法路径轨迹（实验1）Fig.6 Path trajectory of improved ant colony algorithm（E1）

仿真实验环境一是规模为20×20的二维平面，可移动栅格与障碍物栅格比为7∶3，障碍物随机分布。

（b）仿真实验环境二（图7～图9）

仿真实验环境二是规模为30×30的二维平面，可移动栅格与障碍物栅格比为7∶3，障碍物随机分布。

图4～图9是分别是不同环境下传统蚁群算法和本文改进蚁群算法运行10次中规划效果最好的结果，表1是不同实验环境下两种算法搜索结果对比。图4、图7中蓝线表示传统蚁群算法的路径长度收敛曲线，红线表示本文改进蚁群算法的路径长度收敛曲线；图5、图6、图8、图9分别是传统蚁群算法和本文改进蚁群算法在不同仿真实验环境中搜索的所有最短路径和最优路径（即路径最短，转弯次数最少）。由表1可知，在仿真实验环境一中，本文改进蚁群算法与传统蚁群算法相比：最优路径长度减少2.8%，转弯次数减少25%，迭代次数减少47.5%；在仿真实验环境二中，本文改进蚁群算法与传统蚁群算法相比：最优路径长度减少4.9%，转弯次数减少38.5%，迭代次数减少55%。

图5 传统蚁群算法路径轨迹（实验1）Fig.5 Path trajectory of traditional ant colony algorithm（E1）

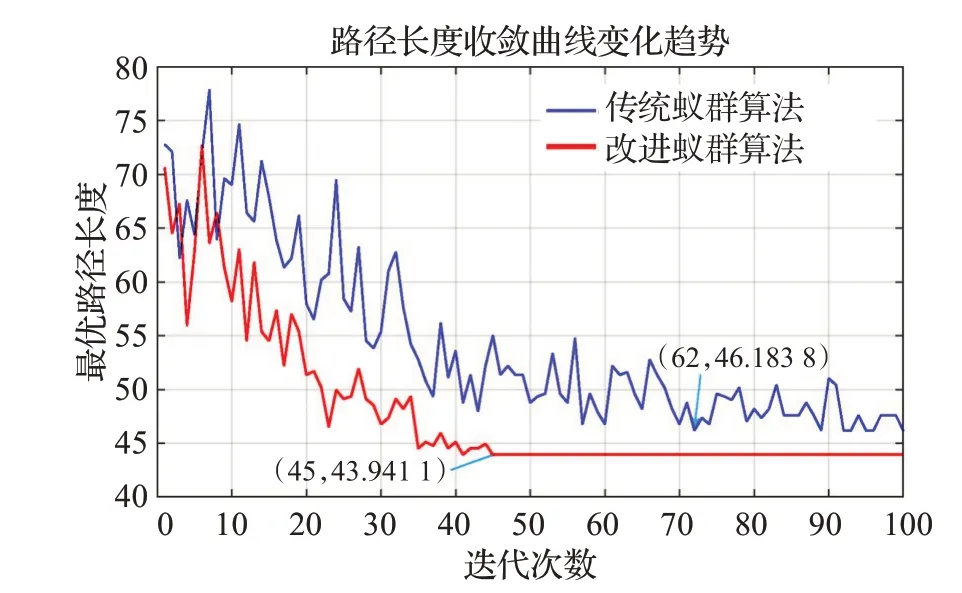
图7 传统与改进蚁群算法的路径长度收敛对比（实验2）Fig.7 Comparison of path length convergence between traditional and improved ant colony algorithms（E2）

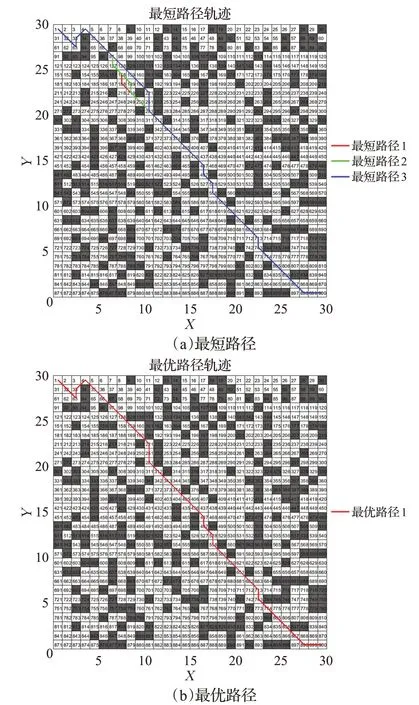
图8 传统蚁群算法路径轨迹（实验2）Fig.8 Path trajectory of traditional ant colony algorithm（E2）

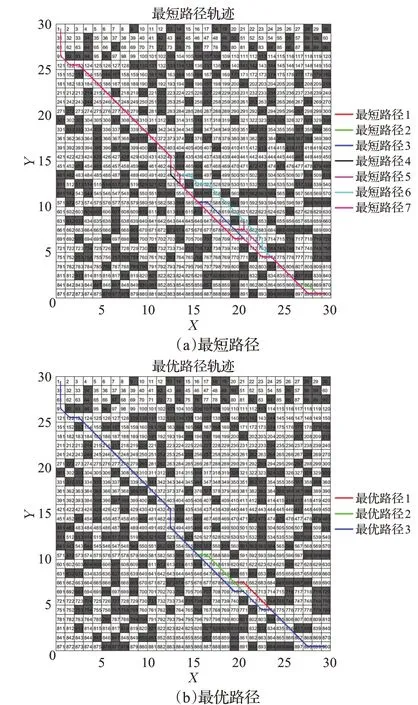
图9 改进蚁群算法路径轨迹（实验2）Fig.9 Path trajectory of improved ant colony algorithm（E2）

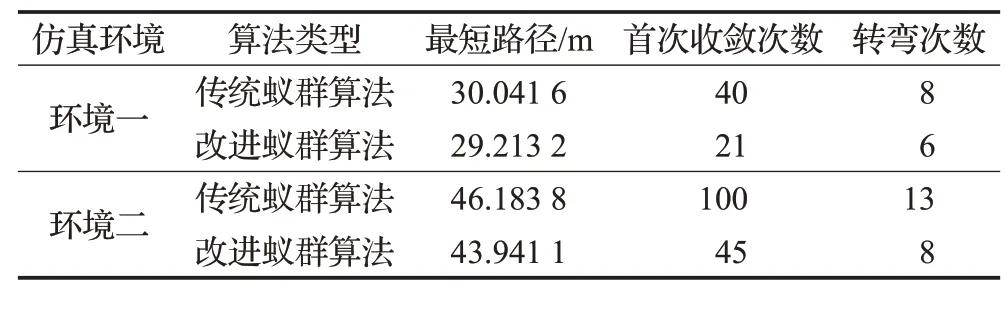
表1 不同实验环境下两种算法搜索结果对比Table 1 Comparison of search results of two algorithms in different experimental environments

通过不同环境下的仿真实验可知，本文提出的改进蚁群算法收敛性更好，规划的全局最优路径质量更优、平滑度更高，证明了本文改进蚁群算法的可行性和有效性。

3.2 基于全局动态路径规划算法的实时路径规划

为了验证全局动态路径规划算法的可行性和有效性，本文在不同模拟环境下，通过Matlab进行传统动态窗口法和本文提出的全局动态路径规划算法仿真实验对比。改进蚁群算法的相关数据参考3.1节；改进动态窗口法的相关数据如下：AGV最高线速度1.0 m/s，最高角速度30.0（°）/s，加速度0.2 m/s，旋转加速度60.0（°）/s，线速度分辨率0.01 m/s，角速度分辨率1.0（°）/s，航向得分的比重0.4、距离得分的比重0.4、速度得分的比重0.2、向前模拟轨迹的时间3 s，距离目标点的距离小于0.5 m时，则认为AGV到达目标点。

（1）仿真实验环境一

仿真实验环境一是规模为10×10的二维平面，可移动栅格与障碍物栅格比为8∶2，障碍物随机分布。本文在栅格地图中设置了两个移动障碍物：红色栅格设为动态障碍物A，蓝色栅格为动态障碍物B。

（2）仿真实验环境二

仿真实验环境二是规模为20×20的二维平面，可移动栅格与障碍物栅格比为8∶2，障碍物随机分布。由仿真实验环境一可知传统动态窗口法在相对简单环境下无法找到目标点，所以本次实验仅做了全局动态路径规划算法。

图10分别表示AGV从遇到动态障碍物B到有效避开动态障碍物B的全过程。图11、图12、图13分别表示传统动态窗口法和本文改进的全局路径规划算法的路径轨迹，其中，图12（a）、图13（a）为全局动态路径规划算法动态路径规划轨迹，图12（b）、图13（b）为改进蚁群算法规划的全局最优路径（红线）与全局动态路径规划算法规划的全局最优路径（蓝线）的对比。由图11可知，传统动态窗口法虽然可以有效躲避移动障碍物，但由于缺少全局信息的指导，陷入死锁，无法成功到达目标点。由图12（a）、图13（a）可知，在全局信息的指导下，本文提出的全局动态路径规划算法可以有效躲避动态障碍物的同时规划出全局最优路径；由图12（b）、图13（b）可知，与改进蚁群算法相比，全局动态路径规划算法规划的路径曲率连续，平滑度更高，更适合AGV的高效运行。

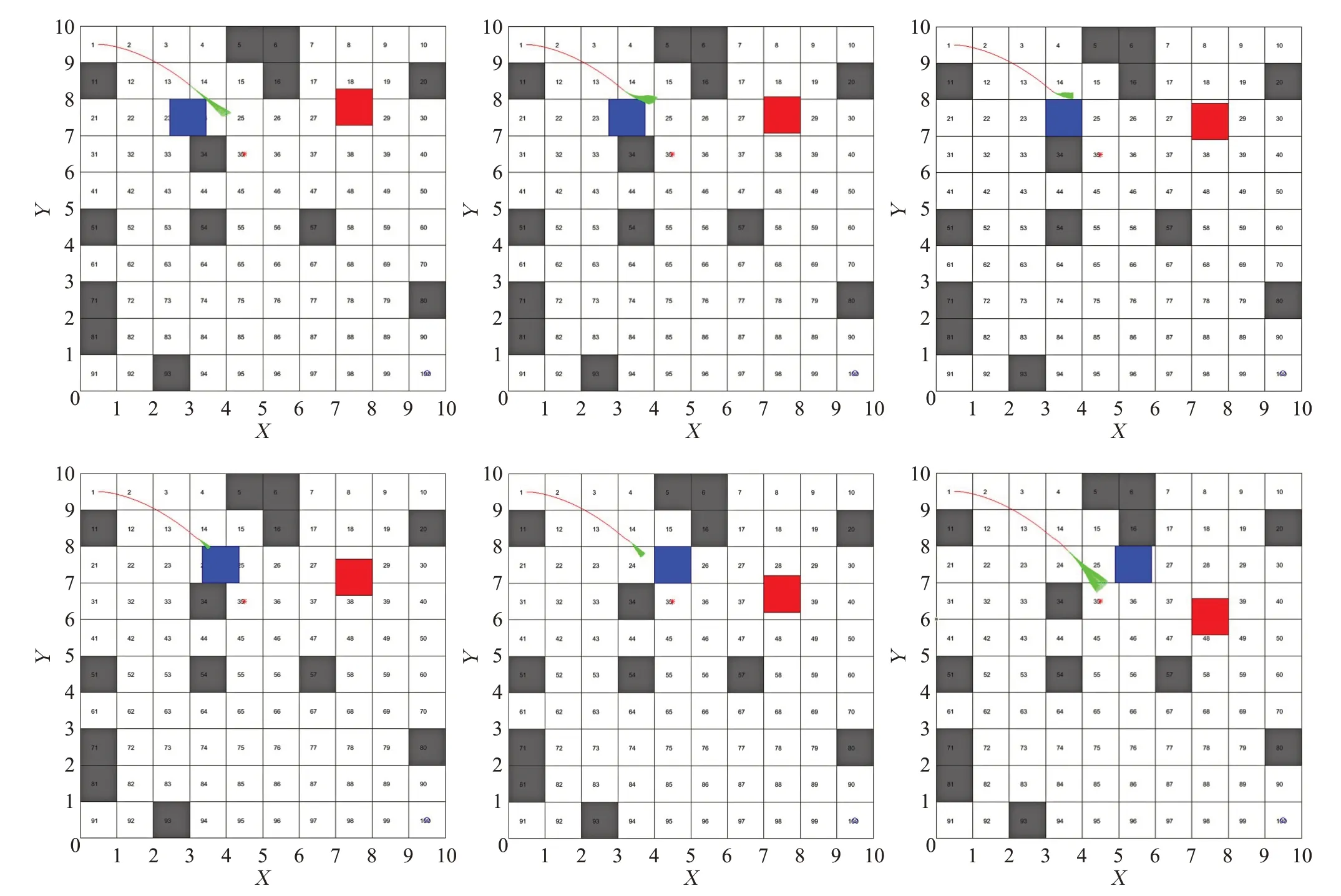
图10 动态躲避障碍物过程Fig.10 Dynamic avoidance of obstacles process

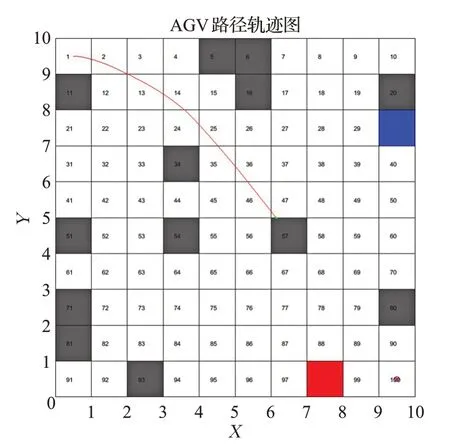
图11 传统动态窗口法Fig.11 Traditional dynamic window approach

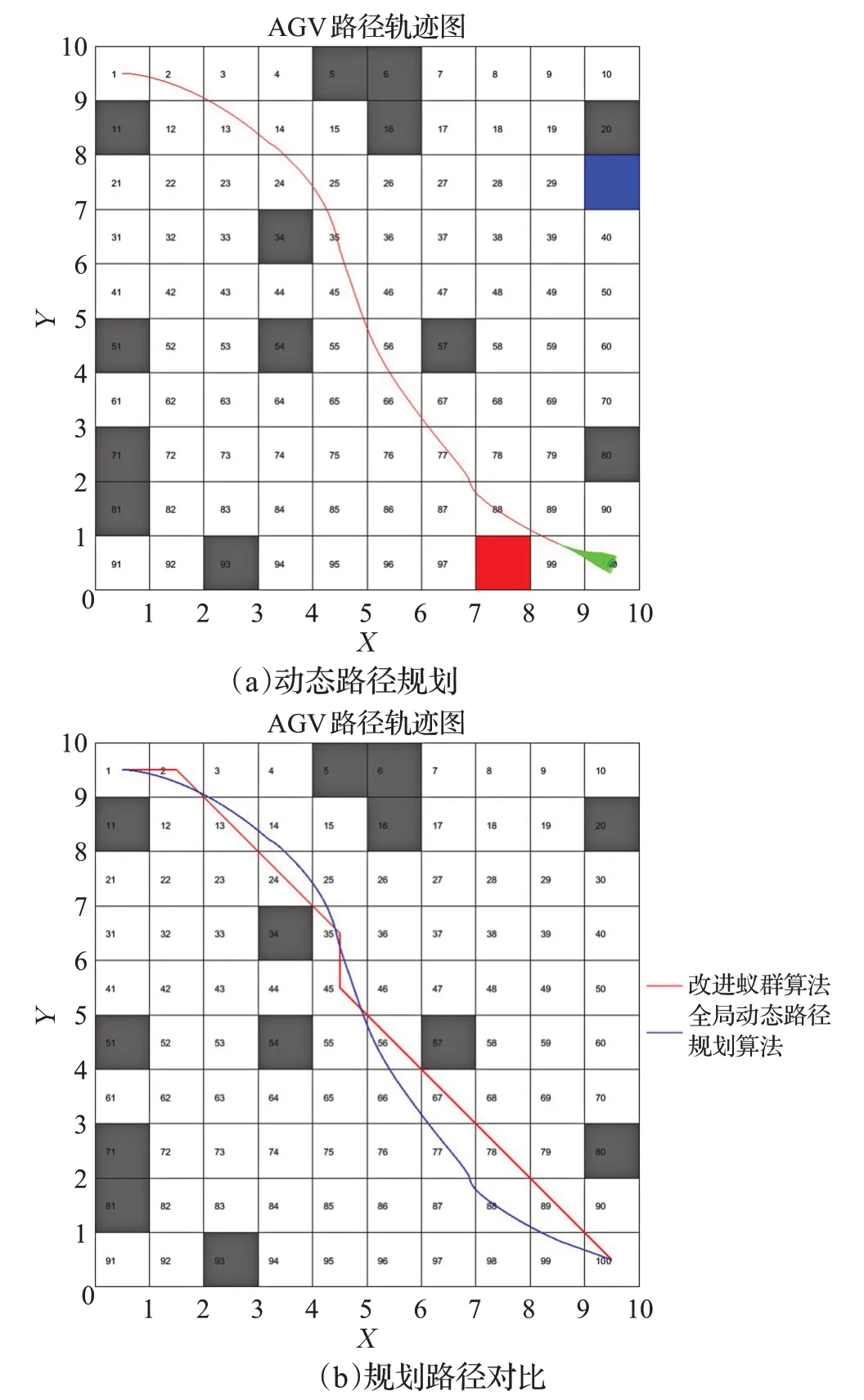
图12 改进的全局动态路径规划算法（实验1）Fig.12 Improved global dynamic path planning algorithm（E1）

图13 改进的全局动态路径规划算法（实验2）Fig.13 Improved global dynamic path planning algorithm（E2）

通过不同环境下仿真实验可知，在全局信息的指导下，本文提出的全局动态路径规划算法在不同环境下都可以通过实时动态路径规划躲避动态障碍物，规划出全局最优路径，证明了本文提出的全局动态路径规划算法的可行性和有效性。

4 结束语

针对全局静态路径规划算法无法有效躲避动态障碍物、局部动态路径规划算法缺少全局环境信息而易陷入局部最优或无法到达目标点等问题，本文提出了一种结合改进蚁群算法和动态窗口法的AGV全局动态路径规划算法。首先，对传统蚁群算法进行改进：（1）基于双向搜索策略提出初始信息素不均匀、双向分布，为蚁群算法双向搜索提供大体方向，避免算法初期存在盲目搜索、收敛性差等问题；（2）针对相邻栅格距离差异较小，本文引入放大系数A来增大相邻栅格的启发信息差异，增大蚂蚁选择更优节点的概率；（3）更新信息素时引入转弯次数影响因素，在所有最短路径中选择转弯次数最少的路径作为最优路径更新信息素，从而得到更平滑的路径，提升AGV运行效率。然后，对动态窗口法进行改进：（1）改进距离评价子函数，以模拟轨迹上各点到障碍物最小距离为评价距离，评价距离越大，表示AGV离障碍物越远，避障效果越好；（2）提出以起点与第一个子目标点的连线与水平方向的夹角动态设置AGV的初始航向角，明确搜索路径的前进方向，避免初始航向角设置不当造成绕行。最后，结合改进的蚁群算法和动态窗口法构建全局动态路径规划算法，以改进蚁群算法规划的全局最优路径上各转折点为动态窗口法子目标点，引导动态窗口法沿着全局最优路径方向进行实时动态路径规划，最终实现AGV在动态环境下沿着全局最优路径躲避动态障碍物。通过不同环境下的仿真实验结果，证明了本文提出的改进蚁群算法和全局动态路径规划算法均可行和有效。