巧用“追问”与“变式” 促进深度学习——以基本不等式应用为例

蔡旦利

(诸暨中学，浙江 诸暨 311800)

苏联教育家乌申斯基曾说：“复习不是为了修补倒塌了的建筑,而是为了加固原来的结构,并且建一新的楼房.”这就告诉我们：复习课不是简单地“炒冷饭”,应从学生的学习需求与现状出发，将复习课上成丰富的、生动的思维构建课，有助于学生知识的提高和升华.而复习课最突出的矛盾就是时间紧，思维量大，要处理足量的题目与充分发展学生思维之间的矛盾，能否处理好这二者之间的关系直接影响到课堂的效果．

波利亚认为，智力的特殊成就是解题，而数学教师的首要任务就是促进学生发展解决问题的能力.波利亚把解题分成4个部分：了解问题、拟定计划、实现计划和回顾.其中,了解问题是指弄清已知数和未知数,条件是什么,可用哪些符号来表述问题；拟定计划是指找到已经解决过的题目与这个题目的联系与区别；实现计划是指解决当前问题，核验每个步骤；回顾包括如何把这个结果或方法进行深度思考和反刍,能否运用到其他题目上去[1].

为实现以上4个部分和谐有序展开,教师通过对题目的条件及结论的不断变形，进行启发式追问，这是促进学生深度学习、建立高质量课堂的有效手段．所谓“变式”教学就是对有关数学概念、定理、习题等在不同视角、不同层次、不同背景下进行变化，有意识地引导学生从“变”的现象中发现“不变”的本质，从“不变”中探求数学规律.其中“追问”就是在教师提问后，学生进行回答，然后教师再根据回答情况进行启发性、有针对性地提问．通过追问可以让学生更好地抓住重点、吃透关键.

求最值是高中数学考查的一块重要内容，其中基本不等式的应用又是常用方法之一.通过加法、乘法、除法和开方等运算，揭示了算术平均数与几何平均数的大小规律，并且通过拓展得出了其他几类平均数之间的大小关系，这是发展学生数学思维的重要载体.它的考查方法灵活多变，在每年的模拟考试乃至于高考中都得到了命题专家的青睐.当然，在复习备考中不能只把问题着眼于各种眼花缭乱的代数形式的变形上，而应该让学生明白为什么要这样变形，这种变形方法又是如何想到的，使学生在碰到新的问题时不会手足无措，懂而不会.

下面笔者以一节关于基本不等式的复习课为例，简单谈谈自己的认识与理解.

上课开始，教师直接给出问题.

例1设实数x,y满足4x2-2xy+y2=8，则2x+y的最大值为______.

几分钟后，教师展示学生的方法：由条件得到

(2x+y)2-6xy=8,

即

从而

(2x+y)2≤32,

于是

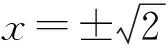
师：怎么想到把条件配凑成2x+y和xy这样的形式呢？

生1：两个数的和可以联想它们的积，把条件配凑成2x，y的“积”与“和”的形式，从而利用基本不等式将“积”转化为“和”，可以直接变为关于2x+y的一个不等关系.

师：那么为什么又把2xy单独放在一边了呢？

生1：这样使得目标更加清晰了.要求的是“和”，因此要把转化对象之“积”放在一边，再转化为目标就行了.

师：其实就是保留“要的”在一边，把另一部分转化为“要求的对象”即可.这个过程中使用了基本不等式的方法，其关键是配凑.

评注该教学过程是为了让学生明白：1)这是求两个数的和的问题；2)和的最值问题可以联想两个数的积；3)如何确保最值能取到，从而建立起应用基本不等式求最值的模式.这显然比教师直接强调“一正、二定、三相等”有效多了.

师：大家还有其他方法吗？对于二元变量问题，可以怎么处理条件？

生2：可以通过条件找两个变量之间的关系，把其中一个变量用另一个量来替换.

师：也就是“消元”的思想.问题是这里的条件是平方关系，消元的话要带根号了，运算起来有些不方便.

生3：可以采用三角换元.先配成两个完全平方之和，即

3x2+(x-y)2=8，

亦即

师：此时x,y都可以用θ表示了，变量也就只有一个了，那要注意什么问题呢？

生3：新变量θ的取值范围要定下来，这个问题中x的取值没有要求，即θ∈R，从而

师：对于有条件的多变量问题，我们往往可以通过条件去“消元”；对于带有平方的式子，配方后进行三角换元也不失为一种好的方法.我们再思考一下还有没有其他方法能够把两个变量变为一个呢？观察一下条件，有什么启发呢？

生4：可以先求(2x+y)2，用常数代入，转化成一个齐次的二次分式形式，即

师：经过这样的处理，形式就比较完美了，分子、分母的每一项都变成了二次的形式.下面如何处理呢？

生4：可以同时除以x2或y2或xy.

师：好的，我们来看一下，比如选择同除以x2，得

生5：可以把分子的二次项“分离”，得

这样就可以用基本不等式了.

师：这里新变量t的取值范围是什么？使用基本不等式的时候要注意什么问题？

生6：t有可能会大于0，也有可能会小于0.

师：这种通过齐次式形式处理为一元的方法很好.可以把这个过程总结如下：

评注三角换元和变齐次式的方法实际上都是将题目中的多变量变为一个，从而使问题更加简洁、明了.

师：在这里我们也可以将目标2x+y看成t，则y=t-2x，代入条件得到关于x的一个一元二次方程

12x2-6tx+t2-8=0.

利用方程有解，通过Δ≥0可得t的取值范围，我们把上述方法称做判别式法.请大家总结一下该方法还可以用在什么问题中？

生7：含有一个二次式的整式问题，把要求的量看成二次方程的系数即可.

评注通过教师的追问和提示，学生从一个例题出发，找到了处理一类问题的方法.通过对题目的分析提炼，洞察题目类型和模式，提升了学生的概括能力和转化能力.

师：如果给原题附加条件x<0,y<0，还能像上面那样做吗？

生8：那应该要发生变化了.比如在配凑法中，(2x+y)2-6xy=8隐含着(2x+y)2>8，因此2x+y的取值范围会进一步缩小；在三角换元中，角θ的取值范围也会受到约束；齐次式中t的范围会变化；最后一种方程思想只考虑Δ≥0还不行，因为x<0，所以要在(-∞,0)上求解.

师：同一类型的问题，条件稍微变化一下，得到的结果就会发生变化.因此，当我们碰到问题时，要注意观察，区别对待.

下面只要分析二次函数复合反比例函数的取值范围即可.

师：那么m的取值范围还是原来的吗？

师：除了这样去消元，条件中的定值1还有其他用法吗？

师：这里角θ的范围呢？

生10：因为m=cos2θ>0,n=sin2θ>0,所以θ∈R,sin2θ∈(0,1],从而

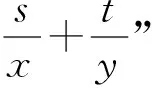
生12：变式1与例1题型相同，只是分母发生了变化，因此可以把条件配成分母的两部分形式.即

再把x+1和my+1看成整体，就变成例1的形式了.

师：很好！变式1给出了最小值，然后求参数的取值范围问题.再来观察一下变式2.

师：变式2与例1相比，不同点在哪里？

生13：分子不是常数了.

师：我们可以怎么处理？

生13：用分离常数法.由

师：对的！这样一转化也变成了原来的问题.

师：变式3中有3个变量，如何处理？

生14：首先还是把分子4y+2z分离，得

已知条件可变形为 2(2y+z)+3(x+z)=6，

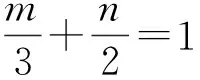
评注有了例1的启发，学生能想到“消元法”，变式3中“逆代法”的结构特征也是比较明显的,因此变式3的解决较顺利.在此，笔者设置变式1～3的目的是：通过对比去挖掘问题的本质，从而提高学生思维的可辨性，培养解题能力.

这样的一节课下来，笔者有两个深刻的体会：1)通过不断地“追问”开拓了学生的思路，从而寻找到新的知识生长点；2)一题多解，一题多变，达到了触类旁通、举一反三的效果，以学生为主的课堂教学模式也得到了体现．同时，关于“追问”，笔者认为：“追问”要精准，紧扣目标，不能空泛；“追问”要精炼，抓住重点，不能零碎；“追问”要有序，由浅入深，顺藤摸瓜；“追问”要灵活，启发思考，直捣黄龙.“追问”的时间节点可以是缺乏思考时或欠缺深度时，甚至是产生歧义时.“追问”能使学生把零碎、散乱、无序的知识主动构建成整体、系统的知识体系.

题目永远是做不完的，但是万变不离其宗，若能善于变式，善于挖掘不同的解题思路，在不断“变”的过程中掌握一类问题的解法，则会大大提高教学效率.“变”与“不变”，都要让学生去经历，通过不断地引导与点拨，让学生去思考和比较，发现问题的本质.只要我们在实践中不断总结、探索、创新，就会找到更多、更好的教学方法．