液压四足机器人单腿的分数阶虚拟模型控制

赵江波，龚思进，马世成，王军政

（北京理工大学 复杂系统智能控制与决策国家重点实验室，北京 100081）

四足机器人因为具有对复杂环境的适应性和灵活的运动方式而成为近些年的研究热点. 不同的足式机器人虽然具有各异的机械结构和驱动模块，但是在控制方法上可以相互借鉴. 虚拟模型控制可以看作是一种引导机制，使用诸如弹簧、阻尼器等虚拟部件将被控系统和期望运动轨迹之间的误差转换成的虚拟力或力矩作为执行机构的期望输入[1]. 在早期的研究阶段，意大利理工学院的HyQ 机器人研究团队和苏黎世联邦理工大学的StralETH 机器人研究团队均采用了基于虚拟模型控制的控制方案[1]，实现了单腿的运动轨迹跟踪和全身的平衡控制[2−3]. 张国腾等[4]利用机器人的基板模型提出了一种映射关系，可以将躯干的受力映射到支撑腿的关节力矩，并将此方法成功应用到机器人的姿态补偿中. 在虚拟模型控制的基础上，意大利理工的HyQ 研究团队设计了基于简化机器人的动力学模型的前馈补偿器，用来调节机器人的高度、速度和身体姿态角[5−6]. 该团队研究表明，采用混合整数凸优化方法[7]同时对步态切换、接触位置以及动作进行优化可以取得更好的控制效果.

MIT 的CARLO 等[8]介绍了一种模型预测控制（MPC）在四足机器人上的实现，该模型可确定扭矩控制的四足机器人的地面反作用力，简化了机器人动力学，以将问题表述为凸优化，实现了机器人前向达3 m/s，侧向达1 m/s 的运动速度. 进一步地，MIT的KIM 等[9]提出了一种结合全身控制（WBC）和模型预测控制（MPC）的控制器，MPC 使用简单模型找到较长时间范围内的最佳反作用力曲线，WBC 根据从MPC 计算出的反作用力来计算关节扭矩、位置和速度命令. 该控制器更专注于反作用力命令，这使它可以完成具有空中相位的高速动态运动. 新设计的WBC 与MPC 集成在一起，实现了Mini-Cheetah 四足机器人高达3.7 m/s 的运动速度.

分数阶微积分可以看作是整数阶微积分的拓展，相比整数阶模型，分数阶模型可以呈现出实际系统更多的特性[10−11]. ZHENG 等[12]用系统辨识的方法建立了永磁同步电机的分数阶模型和整数阶模型，并用实验证明了分数阶模型更接近电机的实际响应，并以此设计了状态观测器. 在控制理论和控制工程领域，以分数阶PID 控制为代表的分数阶控制器在诸多实际工程领域取得了成功的运用[13−16]. 在机器人系统的运动控制中，分数阶PID 控制被用于三自由度的并联执行机构[14−15]. 除了分数阶PID，分数阶微积分与自适应控制以及鲁棒控制相结合的控制方法也在具体工程问题上实现了成功运用[17]. AYTEN等[18]设计了一种新型的基于模型的分数阶自适应PID 控制器，控制器的分数阶项被证明可以增加对于系统不确定性的鲁棒性.

受分数阶微分的启发，提出了一种称作分数阶阻尼的新型虚拟部件，通过将分数阶阻尼与传统的虚拟模型控制相结合，得到了分数阶虚拟模型控制并运用与单腿的轨迹跟踪控制. 传统的虚拟模型控制可以保证机器人与环境的柔性接触，分数阶阻尼的引入被用来提高控制的精确性和鲁棒性. 本文中主要关注虚拟模型控制器的改进和设计在四足机器人小跑运动控制上的运用，并介绍了关节液压缸力控制系统的频域建模过程和基于非线性寻优法的单腿虚拟模型控制器参数整定方法. 通过在实验平台上进行四足机器人的小跑实验，比较虚拟模型控制方法和分数阶虚拟模型控制方法的单腿控制效果，证明了所提分数阶虚拟模型控制的优越性.

1 解耦的分数阶虚拟模型控制

1.1 系统介绍

本实验室自主研制的四足机器人平台如图1 所示，该机器人平台对应的自由度示意图如图2 所示.

图1 四足机器人实验平台和单腿结构Fig. 1 The physical quadruped robot platform and single-leg structure

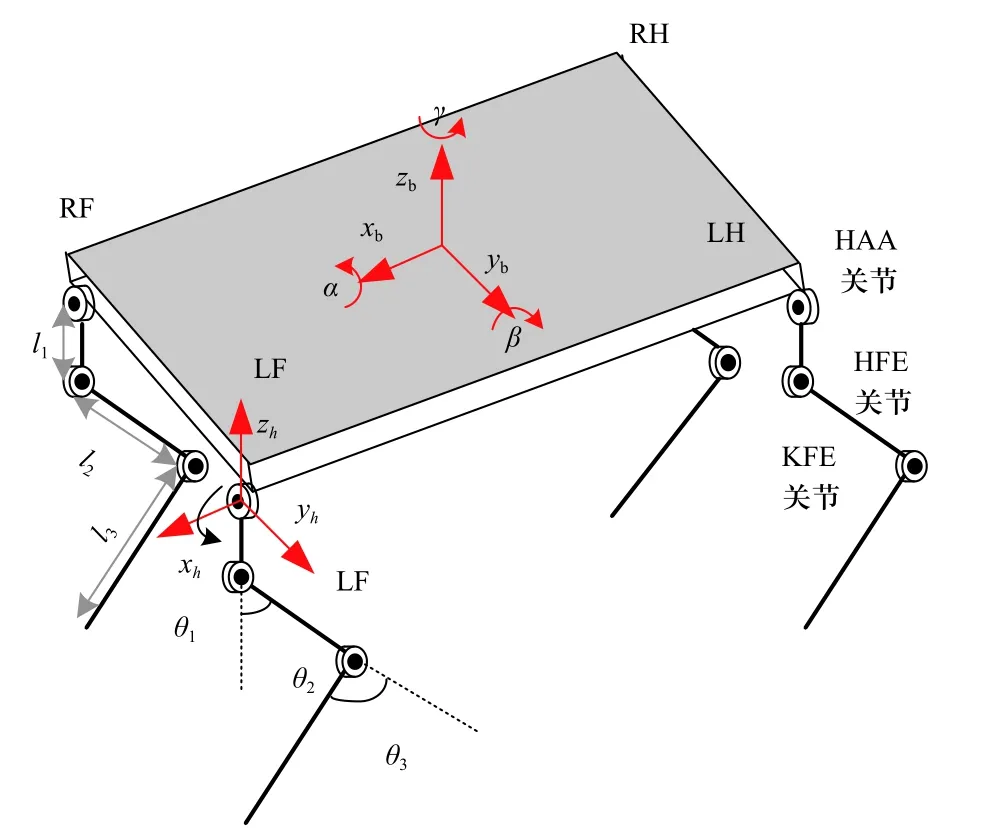
图2 四足机器人自由度示意图Fig. 2 Schematic diagram of physical quadruped robot with 12 degrees of freedom

该模型由一块基板和4 条腿组成，每条腿由上中下3 个肢体组成，基板与每条腿的上肢由髋部横滚（hip abduction/adduction, HAA） 关节相连接，上肢与中肢由髋部俯仰（hip flexion/extension, HFE）关节相连接，中肢与下肢由膝部俯仰（knee flexion/extension,KFE）关节相连接. 全部12 个关节可以由电机或者液压缸驱动. 在对应髋部坐标系 {h}下的足端位置x,y,z可以由3 个关节转角θ1,θ2,θ3和3 个肢体长度l1,l2,l3确定. 除了所有关节对应的12 个可控的自由度，还有6个浮动的自由度，分别是基板的绕xb轴、yb轴和zb轴的旋转自由度，沿xb轴、yb轴和zb轴方向的平动自由度. 小跑运动是四足动物的常见步态，也是四足机器人运动控制的研究热点，该步态可以分解为两组对角腿周期性的完成摆动和支撑运动. 理想情况下，一组腿抬起并开始执行摆动相运动的时候，另一组腿同时触地并开始执行支撑相运动.

四足机器人的小跑运动可以分解成四条腿的支撑相运动和摆动相运动，传统的单腿虚拟模型控制框架如图3 所示.

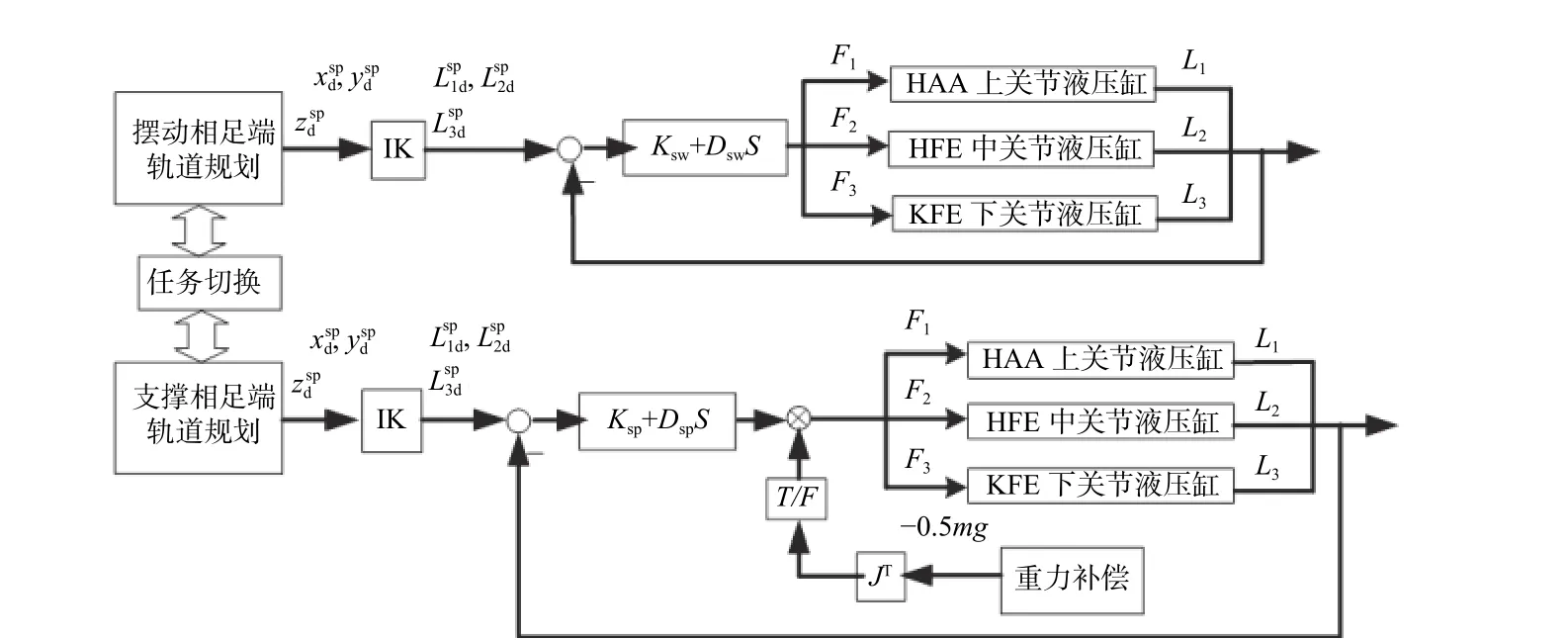
图3 单腿的虚拟模型控制框架Fig. 3 The classical VMC frame for motion control of single leg

IK 为逆运动学解算，足端期望运动轨迹的生成和摆动相支撑相任务的切换由上层的步态轨迹规划器根据时序和足端触地力实现，本文不对足端轨迹规划器的设计做更深入的讨论. 笛卡尔空间的足端轨迹xd,yd,zd可以通过逆运动学的解算得到关节转角空间的期望轨迹θ1d,θ2d,θ3d，再进行一次运动学解算至液压缸长度空间的期望轨迹L1d,L2d,L3d. 在接下的章节中，将详述单腿的解耦VMC 运动控制方案和用分数阶微分对单腿VMC 控制的改进.

1.2 单腿的解耦虚拟模型控制

与文献[4]中将足端点所受的三维虚拟力通过JACOBIAN 矩阵映射到3 个关节力矩的方案相区别，从图3 可以看出，整条腿的运动控制问题被分解成3 个关节的运动控制问题. 本文所基于的四足机器人实验平台的关节采取的是固定于两躯干的可伸缩液压缸驱动方案，HAA 关节处安装有上缸，HFE 关节处安装有中缸，KFE 关节处安装有下缸. 通过数学变换，将三关节转角空间θ1,θ2,θ3中的轨迹跟踪任务和关节力矩控制任务，转换成三液压缸长度空间L1,L2,L3中的轨迹跟踪任务和液压缸力控制任务.

如图4 所示，将三组虚拟弹簧阻尼器施加到单腿的三个液压缸中. 由式（1）所示，每组虚拟弹簧阻尼器可以将缸长误差和缸伸缩速率误差转化为液缸期望力Fi输入

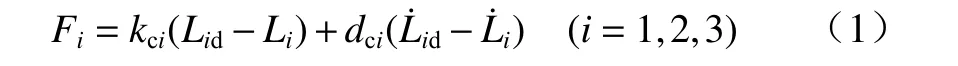
式中：kci为液压缸的虚拟刚度系数；dci为液压缸的虚拟阻尼系数；Li和L˙i为实际液压缸长度和实际液压缸伸缩速率；Lid和L˙id为期望液压缸长度和期望液压缸伸缩速率.

上面介绍了传统文化的发展历程以及它对人类的价值和意义，传统文化历经千百年的洗礼，经受了千锤百炼才以它最美的姿态展现在我们的眼前。但是必须要承认的是，传统文化如今正面临着巨大的挑战，有些非物质传统文化濒临失传，所以现今，能够在景观设计中渗透传统文化，也是对传统文化很好的一个传承。

图5 详细介绍了KFE 关节转角 θ3与液缸长度L3的数学关系，HFE 关节转角 θ2与液压缸长度L2的数学关系和HAA 关节转角 θ1与液压缸长度L1的数学关系可以由相似的过程获得. 为了计算出图3 所示的补偿力矩，需要三个关节力矩到三个关节液压缸受力的转换矩阵FT，FT的计算可以由式（2）所示，h3的计算过程可以参照图4，h1和h2的计算步骤可以遵照相似的步骤.

图4 液压缸驱动关节的虚拟模型控制方案Fig. 4 VMC for hydraulic-cylinder-driven joints

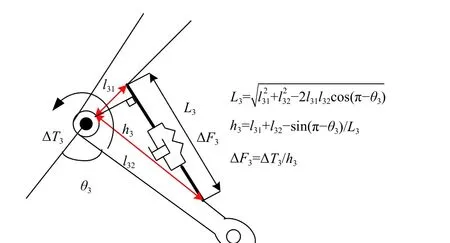
图5 θ3,∆T3 与 L3,∆F3的数学关系Fig. 5 Compute L3 and ∆F3 using θ3 and∆T3

表1 单腿结构参数Tab. 1 The specification of single-leg structure

1.3 引入分数阶阻尼的单腿虚拟模型控制

虚拟模型控制中的虚拟组件既包括简单的虚拟组件诸如弹簧、阻尼、惯性环节等，还有复杂的组件诸如自适应组件和学习组件[1]. 受分数阶微分的启发，提出了一种分数阶阻尼. 传统的虚拟模型控制以牺牲精度为代价保证机器人与地面的柔性接触，但是精度的牺牲会对整体行走效果产生负面影响. 于是将传统的虚拟模型控制与分数阶阻尼相结合，用来增加单腿控制的精确性和鲁棒性[14−15].

GL 定义下的分数阶微分由式（4）表示

因为HAA 关节主要承担侧摆运动和横滚角补偿，对于机器人的前进没有直接作用. 为了简化单腿控制器的设计，仅在HFE 关节和KFE 关节处对应的中缸和下缸位置控制器处添加分数阶阻尼环节. 综上，单腿的解耦分数阶阻尼虚拟模型控制由式（7）和式（8）表示.

2 分数阶虚拟模型控制器的设计

2.1 基于优化法的参数整定

如图3 所示，支撑相控制系统和摆动相控制系统均包含基本的液压缸位置控制系统. 提出的分数阶虚拟模型控制在数学上与液压缸位置的PDDλ控制等效，基本的如图PDDλ控制框图6 所示，由被控系统G(s)和PDDλ控制器C(s)组成，包含4 个待整定的参数：比例增益ki，微分增益di，分数阶微分增益 dfi，分数阶次 λ.

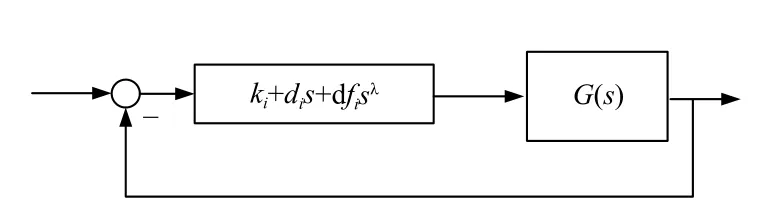
图6 典型的PDDλ 控制系统框图Fig. 6 Typical block diagram of PDDλ control system

作为经典的分数阶控制器参数整定方法，基于频域响应的控制器参数整定方法[19−20]在开环控制系统C(s)G(s)的频域特性分析的基础上，选取若干决定整个控制系统稳定性和鲁棒性[21−22]的频域指标，采用优化的方法找到一组最符合频域指标的控制器参数. 由于实际被控系统G(s)的精确模型难以得到，因而被控对象的频域特性通常由频响实验测得.

根据BODE 相对稳定裕度理论，增益交越频率为开环系统增益为1 时的角频率，增益交越频率的选取会对闭环系统的稳定时间造成影响. 在确定增益交越频率之后，选取相角裕度和等阻尼特性作为频域指标. 相角裕度条件要求开环系统在增益交越频率距不稳定界限的相位大于一定的值. 等阻尼特性要求开环系统的相角变化率在处为0，表示闭环系统C(s)G(s)对于G(s)增益变化的鲁棒性.

2.2 被控对象的频域特性获取

单腿的中缸和下缸的外环位置控制系统框图和带负载的内环力控制框图如图7 所示，由于难以得到电液伺服系统的精确数学模型，用频响实验获取带负载的液压缸力闭环控制系统的频率响应. 通过施加正弦力期望值信号到带负载的中缸力控制系统和下缸力控制系统，可以得到相应的液压缸位置输出信号，并计算出两者的幅值比和相位差作为带负载的液压缸力控制系统在特定频率下的增益值和相角值. 之后采用最小二乘法，使用带负载的液压缸力控制系统在不同频率下的增益和相角，拟合出两个关于角频率的三次多项式，分别代表液压缸力控制系统的增益频域特性和相角频域特性.

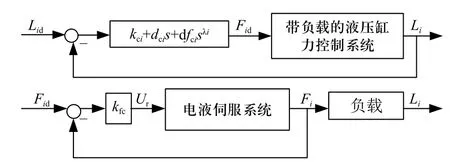
图7 液压缸位置PDDλ 控制Fig. 7 Cylinder position PDDλ control block diagram

2.3 sλ在实际工程中的近似

Oustaloup 滤波器近似法是一种经典的用高阶整数阶传递函数近似分数阶微分算子的方法[22−23].Oustaloup 近似传递函数由式(11)所示

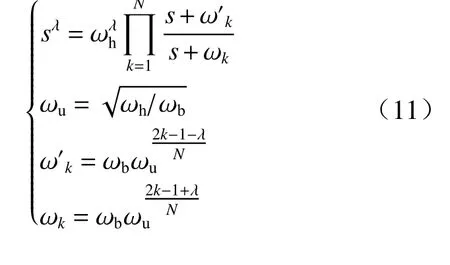
式中： ωh为角频率上限； ωb为角频率下限；N为分数阶阶次，在感兴趣的频段[ωb,ωh]近似sλ的频域特性[20].由于控制器采用Matlab 实时系统，因此在Simulink环境下很容易用Oustaloup 传递函数替代sλ，方便控制器的搭建. 本实验选取N=5，ωh=1 000 rad/s，ωb=0.01rad/s.

3 实验结果和讨论

3.1 实验平台硬件

图8 显示了实验设备和实验环境，控制盒（a）包含一块运行Matlab 实时系统的PC104 作为主控制器，接受来自姿态传感器（b），内嵌式位置传感器以及力传感器（e）的输出信号，发送控制输入信号到电液伺服阀（c）来控制液压缸（d）. 主控制器通过WiFi 模块与监控上位机（g）相连，记录所测量的液压缸位置以及姿态角. 所有液压缸均由液压油源（f）供能，压强定为5 MPa. 在Simulink 环境中搭建PDDλ控制器和足端轨迹规划器，并将这些模块载入主控制器中. 支撑相和摆动相的液压缸位置的期望轨迹由步长、步高、步态周期和规划方法决定. 在本实验足端轨迹规划器设计中，设置步长10 cm，步高5 cm，步态周期1 s，并选择0 冲击摆线规划.

图8 实验平台硬件和实验环境Fig. 8 Experimental setup and environment

3.2 控制器参数整定结果

通过给中缸力控制系统和下缸力控制系统分别施加1～4 Hz 之间13 个不同频率的正弦期望力信号，并计算出中缸力控制系统和下缸力控制系统在13个频率输出信号和期望信号对应的幅值比和相位差，结果如图11 和图12 所示.

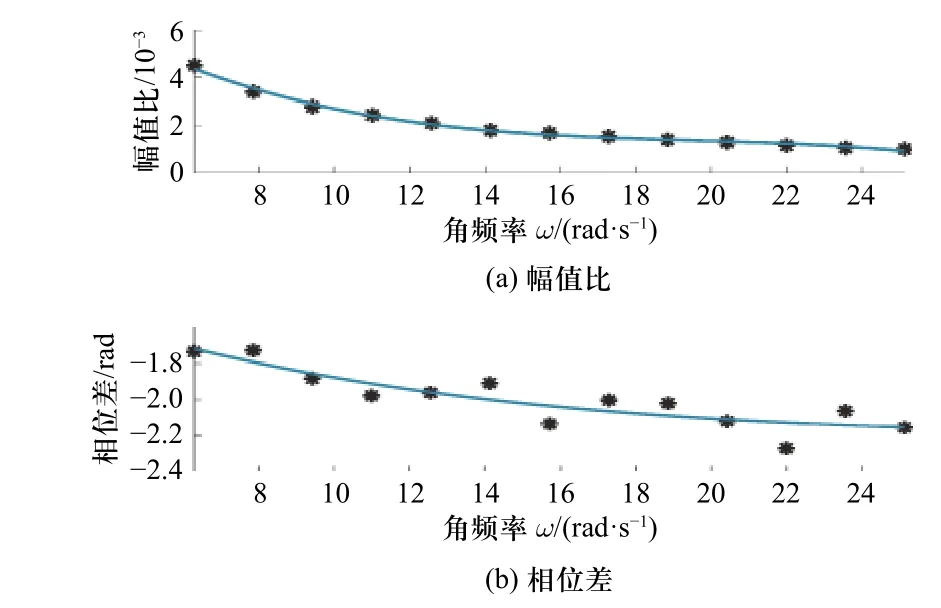
图9 中缸的幅频特性和相频特性拟合曲线Fig. 9 The fit curve of mid cylinder frequency domain characteristics

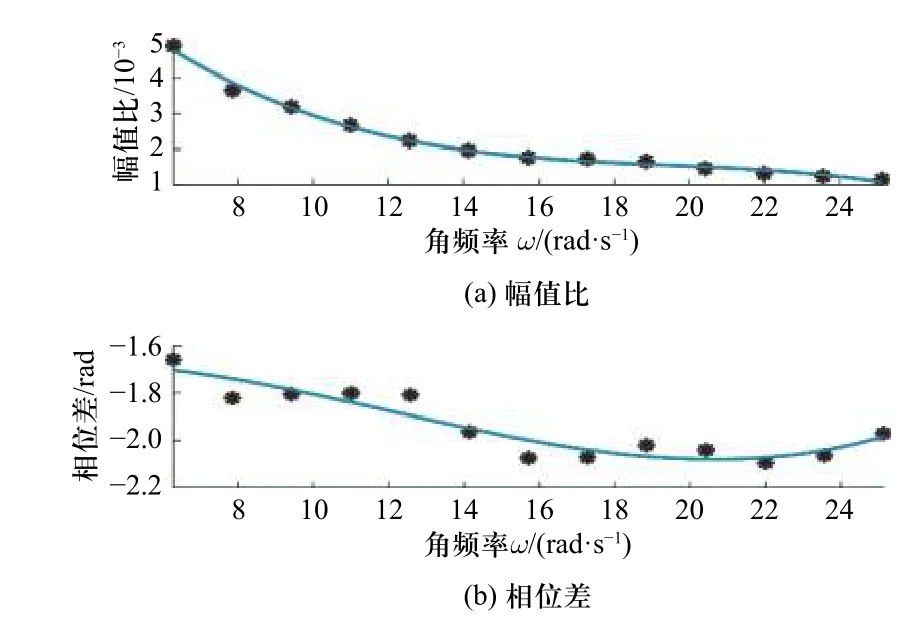
图10 下缸的幅频特性和相频特性拟合曲线Fig. 10 The fit curve of lower cylinder frequency domain characteristics

用最小二乘法将所得13 组角频率和幅值的数对，13 组角频率和相角的数对拟合成两个关于角频率ω的三次多项式，用来描述带负载的液压缸力控制系统的幅频特性和相频特性. 式（12）描述带负载的中缸力控制系统的幅频特性方程和相频特性方程，式（13）描述带负载的下缸力控制系统的幅频特性方程和相频特性方程.

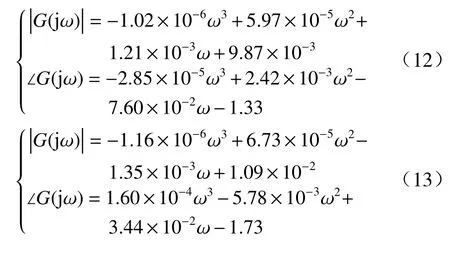
得到中缸力控系统和下缸力控系统的相频关系和幅频关系之后，结合2.1 节介绍的优化整定方法，可以得到中缸和下缸最优的分数阶虚拟模型控制器参数，如表2 所示. 由于四足机器人的每条腿都具有相同的机械结构和驱动系统，所以一条腿的控制器的参数整定结果可以适用于其他三条腿.

表2 优化分数阶虚拟模型控制器参数Tab. 2 Optimized FOVMC parameters in experiment

3.3 实验结果

利用上一节优化所得的控制器参数为参考并结合人工整定，所得最终的实验控制器参数如表3 所示. 为了证明所提出分数阶虚拟模型控制的有效性，比较了分数阶虚拟模型控制和传统虚拟模型控制的单腿轨迹跟踪效果和触地力大小. 在传统的虚拟模型控制中，存在触地力与跟踪误差的矛盾，因为高精度的跟踪会导致较大的触地力继而对身体的平衡造成扰动. 故而采用单腿轨迹跟踪误差和触地力两个指标来衡量单腿控制效果.

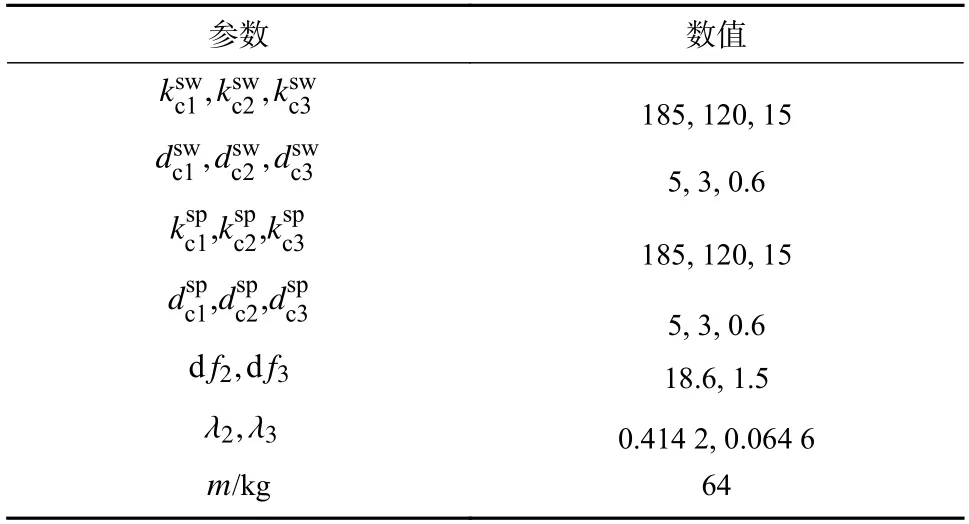
表3 控制器和姿态补偿器参数Tab. 3 FOVMC controller and attitude compensator parameters

图11 显示了机器人在分数阶虚拟模型控制和传统虚拟模型控制控制下的平地前向小跑实验的结果图，包含了单腿的实际液缸位置曲线和期望液压缸位置起曲线以及足端触地力曲线.

图11 液压缸跟踪效果Fig. 11 Cylinder length tracking performance

两种方法控制下的中缸跟踪误差和下缸跟踪误差的绝对值如图12 所示，表4 中列出了中缸和下缸的轨迹跟踪均方误差. 结果显示在足端产生触地力大致相等的前提下，分数阶虚拟模型控制可以有效减小中缸和下缸跟踪过程中的最大误差和均方误差，在保证柔性接触的同时提高了单腿轨迹跟踪精度.

表4 比较两种控制器的跟踪均方误差Tab. 4 Tracking performance of both VMC and FOVMC

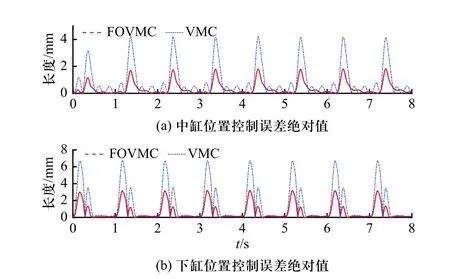
图12 液压缸跟踪误差Fig. 12 Cylinder length tracking error

4 结 论

在本文中，提出了四足机器人的分数阶虚拟模型控制，并介绍了针对本实验室液压四足机器人的控制器参数整定方法和液压缸力控制系统频域特性的建模过程. 在液压四足机器人平台上进行小跑实验，通过实验比较了分数阶虚拟模型控制和虚拟模型控制的单腿轨迹跟踪效果，跟踪均方误差减少了约82.4%，证明了分数阶虚拟模型控制对于单腿轨迹跟踪的改善效果.

在以后的研究中，将建立四足机器人的全身动力学模型，并基于动力学模型设计姿态力矩补偿器，将这个补偿器与现在的分数阶虚拟模型框架组合，进一步改善四足机器人的运动控制效果.