基于混合建模方法的车用比例电磁阀热效应影响分析

任延飞，席军强，陈慧岩，马锴文

（北京理工大学 机械与车辆学院，北京 100081）

比例电磁阀作为车用自动变速箱（AT）电液换挡执行系统的先导控制元件，其作用是将来自TCU 的控制指令精确、稳定的转换为液压控制信号，是换挡系统的关键部件之一[1−2]. 它的响应速度、输出油压的稳定性及油压-电流的线性度等特性会影响换挡系统的性能，大多数的研究集中在电磁阀的模型分析[3−6]、优化设计[7−9]和精确控制[10−12]等方面. 然而，电磁阀在工作过程中线圈会产生大量的焦耳热，当温度升高时，线圈绕组的电导率下降，而电磁阀结构在热应力的作用下也会发生不同程度的应变. 再加上工作环境（冲击、振动等）影响，容易使得绕组外的绝缘漆出现磨损，最终导致电磁阀的失效[13−14].

刘艳芳等[15−16]通过有限元方法建立了电磁阀多物理场耦合模型，对电磁场、温度场进行仿真分析，研究了电磁阀在不同环境温度下线圈内部与外部的温差. CHENG 等[17−19]对超高速响应电磁阀进行有限元仿真，分析了在不同控制策略下的功率损耗与电磁阀温升的关系. ZHAO 等[20−21]分析了高速开关电磁阀在不同驱动电压、电流时的功率损失，其中，线圈的焦耳热功率占总损失功率的50%以上，但该研究未进一步研究温度场特性. 李剑锋等[22]通过建立电磁铁有限元热结构仿真模型，得出线圈在热应力和机械应力的共同作用下发生疲劳失效.

目前，对电磁阀热效应的研究主要集中于线圈发热对其寿命的影响，忽视了热效应对其结构特征和系统动态特性的影响. 因此，为了能够准确地分析内、外温度场引起的热效应对系统动态性能的影响，本文提出了一种基于有限元方法与系统动力学方程混合建模的分析方法. 以某种自动变速箱用比例电磁阀为研究对象，首先，建立比例电磁铁的多物理场有限元模型，分析不同环境温度和工作条件下的温度分布、应力分布及应变情况，得到包含温度变量的数据集；其次，将上一步得到的数据集与系统动力学方程相结合，建立包含温度的系统动态模型，分析温度场对动态特性的影响；最后，通过试验验证了该方法的准确性和可行性.

1 比例电磁阀结构与耦合分析

1.1 结构与工作原理

图1 为某自动变速箱用高速比例电磁阀的结构图，从功能特性上可以分为两部分，一是电磁铁组件，二是液压组件. 其中，电磁铁组件主要包括线圈、外壳、前轭铁、后轭铁、衔铁、弹簧、调整螺钉等部分；液压组件主要包括阀体、挡板阀芯、球阀芯等部分.

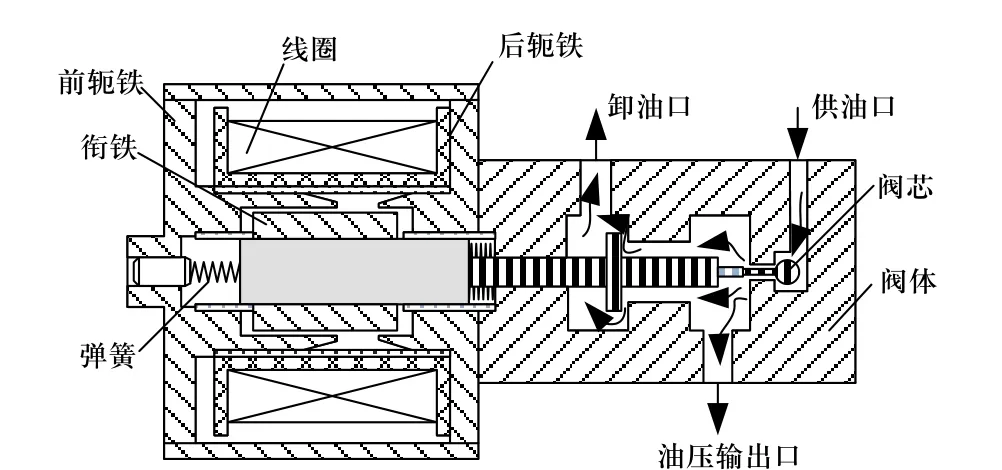
图1 比例电磁阀结构简图Fig. 1 Structure diagram of proportional solenoid valve

当线圈通入电流时，生成磁场，产生电磁力. 由于隔磁环的分磁作用，使得衔铁所受轴向电磁力与电流近似呈线性增长. 衔铁在电磁力的作用下推动挡板阀芯与球阀芯向前运动，油液从球阀芯处流入，一部分进入工作腔，另一部分从卸油口流出，直到工作腔内的压力达到平衡. 通过调节电流的大小，可以使衔铁获得不同的电磁推力，从而调整球阀芯与挡板阀芯处的开口量，进而得到不同的输出油压. 当电磁阀断电时，衔铁上的电磁力消失，球阀芯在液压力的作用下，推动挡板阀芯与衔铁回到原位.

1.2 耦合关系分析

比例电磁阀是一个强非线性的多物理场耦合系统，按照信号的传递路线，将电磁阀分成以下6 部分：电场、磁场、温度场、结构力学、系统动力学及流场，如图2 所示. 具体耦合关系分析如下：

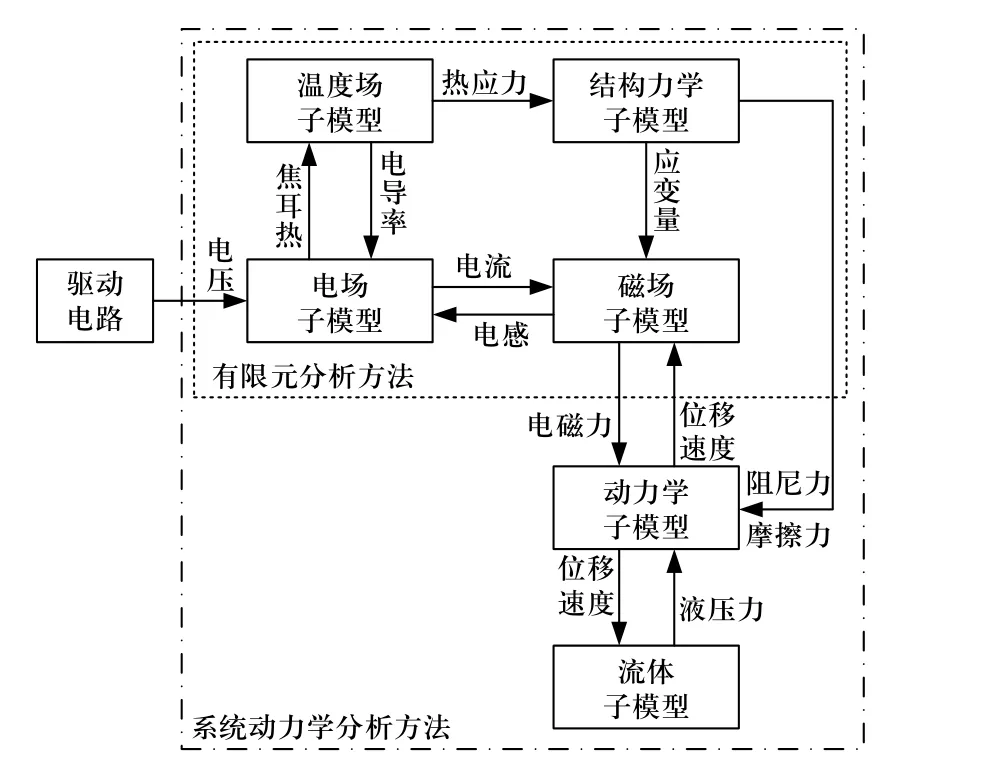
图2 比例电磁阀多物理场耦合示意图Fig. 2 Schematic diagram of multi-physics coupling of proportional solenoid valve

①当驱动电路有电压输出时，电场内部产生电流；电流经过线圈形成磁场，并产生电感反作用于线圈，降低电流的增长速度；同时，磁感线在外壳、前轭铁、衔铁、后轭铁之间形成闭环，并产生电磁力；

②线圈内部会产生焦耳热，与环境温度共同作用于结构内部，形成温度场，并在材料内部产生热应力；同时，温度场又反作用于线圈，使电导率降低；

③电磁铁的结构材料在热应力的作用下发生变形，从而使得电磁力、电感和动力学参数（阀芯运动的阻尼系数、摩擦力等）发生变化；

④运动部件（衔铁、推杆和阀芯）在电磁力、阻尼和流场液压力的作用下产生加速度、速度和位移. 当忽略温度场影响时，系统在相同工作条件下的系统动力参数是一致的. 当考虑温度场影响时，运动部件所受的电磁力、阻尼力、摩擦力都会发生变化，从而影响系统输出的状态和稳定性；同时，位移、速度又反作用于磁场和流场，分别影响电感、电磁力和液压力.

2 模型建立

本文提出的比例电磁阀混合建模分析方法可以分为两部分：一是基于FEM 建立比例电磁铁的电磁场、温度场和结构力学的分析模型，探讨温度场对电磁铁输出特性的影响，得到包含温度场的数据集（电磁力、电感）；二是将第一步得到的数据集带入系统动力学方程，建立比例电磁阀的系统动态模型，深入分析温度场对系统动态特性的影响.

2.1 电磁铁有限元模型

2.1.1 电磁场子模型

基于麦克斯韦尔方程建立电磁铁的有限元模型时，其基本方程为

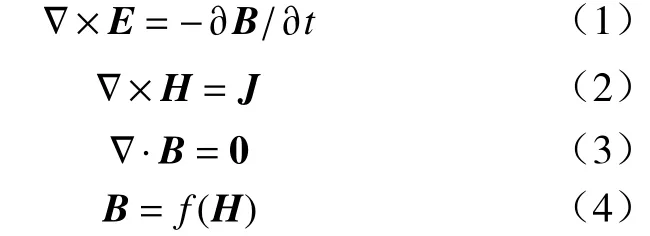
式中：B为磁感应强度；H为磁场强度；J为电流密度矢量；E为电场强度.

2.1.2 温度场子模型

电磁铁在工作过程中，能量损失不可避免，大部分以热量的形式散失，导致结构温度升高. 通过式（5）～（8）计算出各部分的温度，如图3（b）所示.

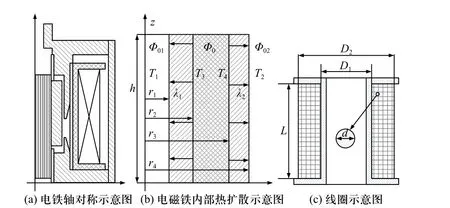
图3 电磁铁热传导示意图Fig. 3 Schematic diagram of electromagnet heat conduction

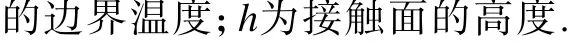
2.1.3 结构力学子模型

随着结构温度的升高，根据胡克定律，材料在受热时内部会产生热应力，从而导致结构发生不同程度的热应变. 根据式（10）～（13）计算结构应力、应变与温度的变化关系. 根据弹性力学理论，几何方程为

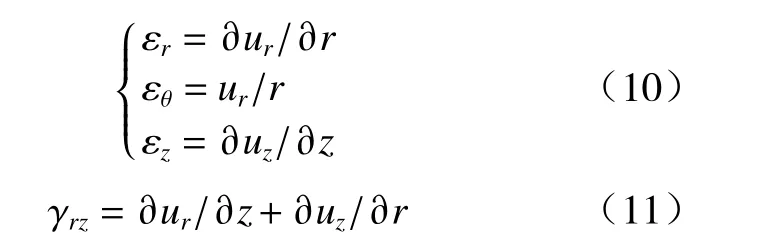
式中:ur为沿r方向的位移；uz为沿z方向的位移；ɛ为正应变；γ为切应变. 根据胡克定律，材料的弹性方程为

2.2 系统动力学模型

2.2.1 动力学子模型

将机械运动部件看作由质量、弹簧和阻尼组成的二阶系统，其动力学方程通过式（14）进行描述:

式中：R为电路中的阻值；i为线圈电流； ψ为磁链，与电流大小、气隙及时间有关；L(x, i, T)为电感；x为衔铁位移.

对于比例电磁铁，衔铁在工作行程内所受到的电磁力大小与电流近似呈线性关系，而与位移无关，因此，通过2.1 节的有限元模型得到电磁力与电流、温度的非线性函数为

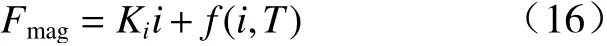
式中：Ki为电流增益系数；f(i,T)为电磁力温度修正函数，与电流大小和温度有关.

2.2.3 流场子模型

流场部分采用球阀与挡板阀组合的结构形式，如图4 所示，通过改变阀芯位移两个节流口的开度，从而改变工作油口的输出油压. 假设供给口压力为常数0.65 MPa，卸油口压力为0 MPa. 根据阀门出口流量公式（17），计算控制端口净流量为

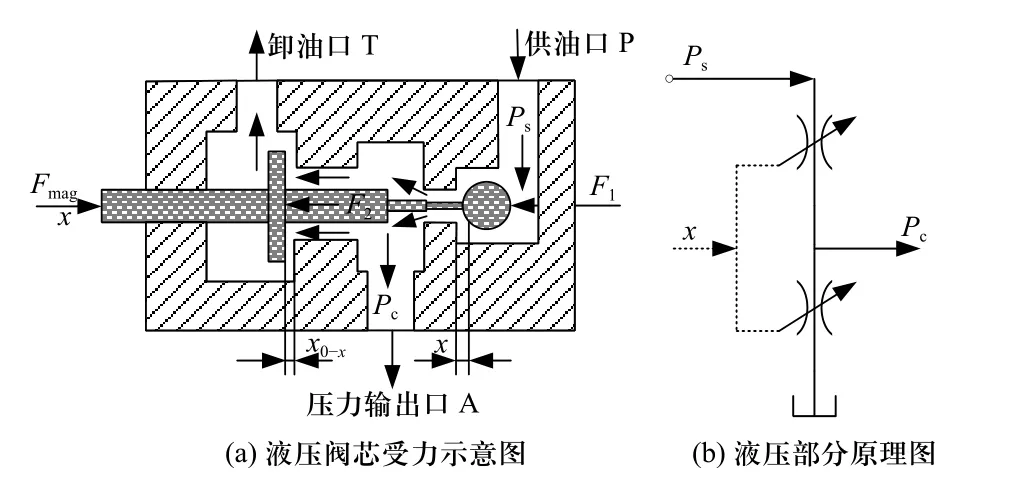
图4 流体部分结构原理图Fig. 4 Schematic diagram of the fluid structure

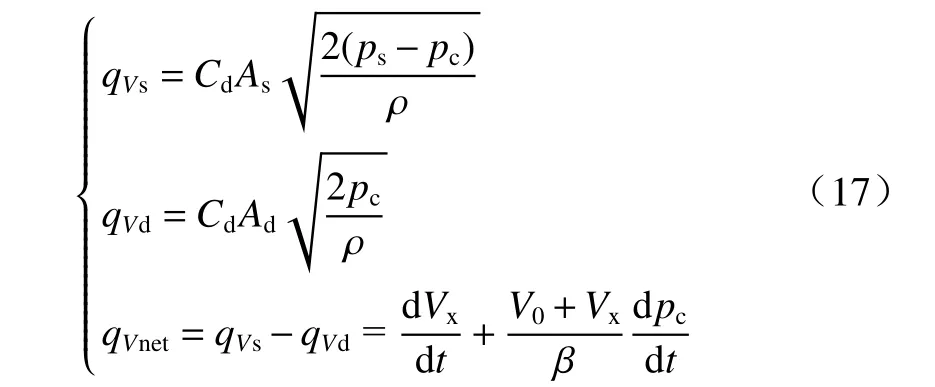
式中：qVs为阀芯进油口处的流量变化；qVd为阀芯卸油口处的流量变化；qVnet为进入工工作腔内的净流量变化；Cd为流量系数；ρ为油液密度；As为进油口出的过流面积；Ad为卸油口的过流面积；ps为供油压力；pc为输出压力；V0为初始体积；Vx为体积变化量.

阀芯受到的液压力可以分为两部分：球阀受力与挡板受力，受力分析得：

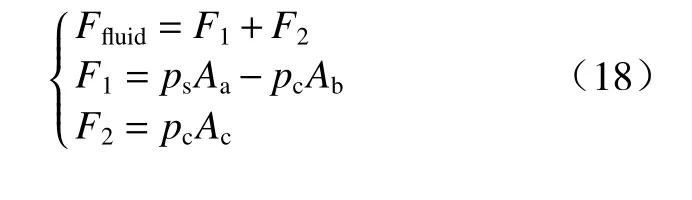
式中：F1为球阀芯受到的液压力；F2为挡板阀芯受到的液压力；Aa为ps的作用面积；Ab和Ac为pc的作用面积.

2.3 耦合计算过程

图5 所示为比例电磁阀多物理耦合计算流程图，该过程分成两部分，每一部分都采用循环迭代方法进行计算，具体解析如下：

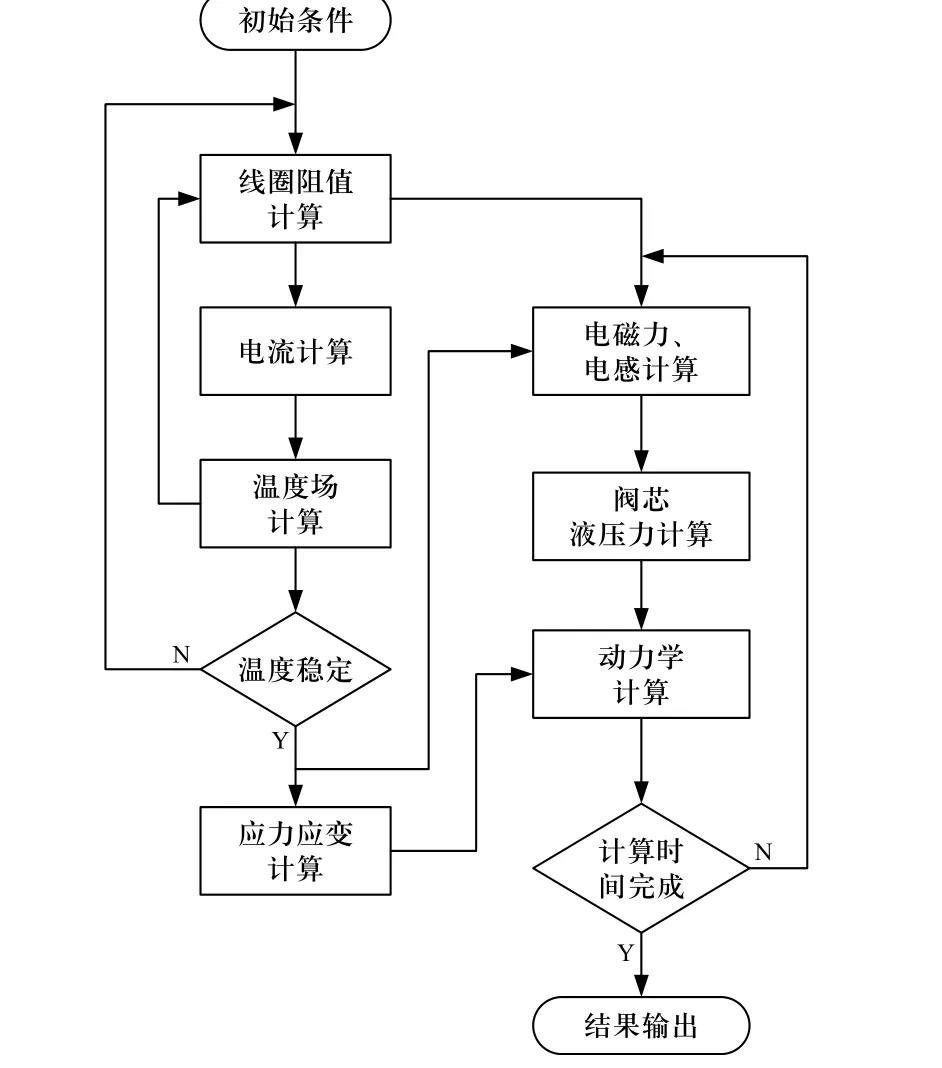
图5 多物理场耦合计算程序示意图Fig. 5 Schematic diagram of multi-physics coupling calculation program

①根据2.1 节建立的有限元稳态分析模型，分别计算不同环境温度和不同输入电压时的稳定电磁力、电感、电阻、电流、温度之间的关系. 由于在不同环境温度和不同输入电压下的温度场分布不同，每一步计算的温度值与上一步结果进行对比，直到温度达到稳定，输出计算结果；

②运动组件的系统动力学与电磁场、温度场等的耦合过程比较复杂：运动组件在电磁力、阻尼力、摩擦力和液压力的共同作用下发生运动，而电磁力由电磁场产生，并与结构参数和阀芯位置相关，同时阻尼力和摩擦力也受结构参数有关. 由于温度场使得结构参数发生变化，因此，电磁场输出的电磁力、阻力力和摩擦力都会发生改变，进而影响阀芯的运动状态.

根据2.2 节建立系统动力学分析模型，其计算过程步骤如下：①初始化系统模型的输入条件，包括电压、环境温度、输入油压等，并计算阀芯到的作用力；②下一时刻，随着电流的增加，线圈的温度增加，导致线圈参数和结构参数发生变化，从而导致电磁力、阻尼力等也发生变化，计算出阀芯的位移、速度和加速度，并反馈到电磁子模型中；③下一时刻，重复第二步计算，直到仿真时间结束，输出仿真结果.

3 温度场分析

根据2.1 节构建的比例电磁铁有限元模型，采用COMSOL Multiphysics 仿真平台对比例电磁铁进行电-磁-热-结构力学的多学科仿真. 设置环境温度为20 ℃，仿真输入电压分别为1～12 V（间隔1 V）时的稳态结果，现以3，6，12 V 3 种电压输入方式为例，进行热固耦合分析. 由于温度特性的影响，此时线圈内的工作电流分别是0.53，0.91，1.36 A.

根据比例电磁铁的稳态温度分布图6（a）～6（c）所示，在3，6，12 V 的电压输入条件下，线圈的最高温度分别是38，79，211 ℃，并且都集中在线圈内部；其次是外壳的圆柱面上的温度比较大，而最低温度集中在后轭铁的端面. 线圈作为温度场的热源，热量通过结构材料向外传导，因此，材料的热传导系数和环境温度对温度分布有很大影响. 由于线圈在设计时的最高耐热温度为180 ℃，因此，在12 V 的电压下长期工作会使得线圈烧毁.

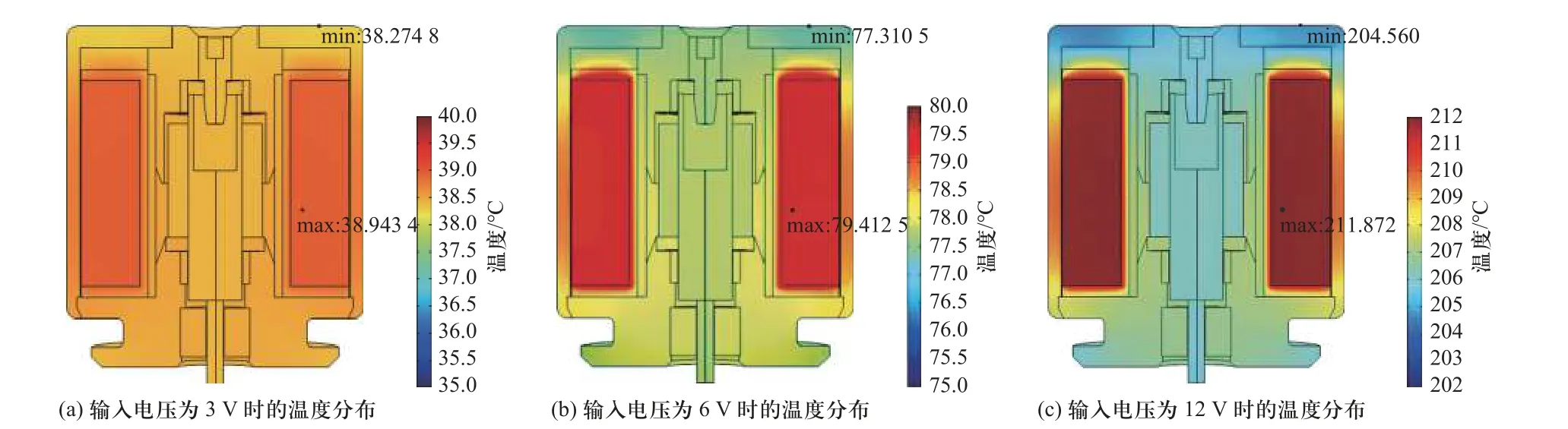
图6 电磁铁稳态温度场分布图Fig. 6 Electromagnet steady-state temperature field distribution diagram

根据比例电磁铁的稳态应力分布图7（a）～7（c）所示，当温度达到稳态时，最大应力值分别是22，48和202 MPa，应力大的区域主要集中在外壳的圆柱面，以及外壳与前轭铁的接触处.

图7 电磁铁整体的应力分布Fig. 7 The overall stress distribution of the electromagnet

通过分析线圈内部应力分布图8（a）～8（c）可见，线圈内部的应力分布不均匀，最大应力分别是9，23和68 MPa，主要集中在线圈与骨架的接触处. 由于线圈骨架和绕组件填充物的热膨胀系数大，线圈发热时产生较大的变形，从而降低绕组间紧密度，再加上外部环境的振动，容易使绕组的绝缘漆发生磨损，最终导致线圈短路失效.

图8 线圈的应力分布Fig. 8 Stress distribution of the coil

图9（a）～9（c）和图10（a）～10（c）所示的分别是外壳、前轭铁、后轭铁和铜套组合的应力分布图和应变分布图. 由于外壳与铜套的材料不同，使得外壳边缘产生一定的弯曲，对应的应变量分别是0.009，0.012和0.043，导致隔磁环处的结构参数发生了变化. 结果表明，温度越高，隔磁环处的结构参数变化越大.

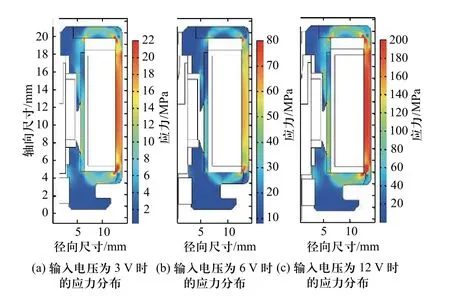
图9 隔磁环结构的应力分布Fig. 9 Stress distribution of the magnetic isolation ring

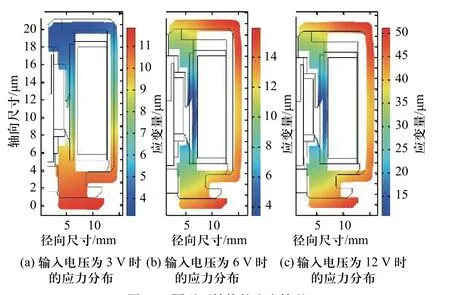
图10 隔磁环结构的应变情况Fig. 10 Strain situation of the magnetic isolation ring

上述研究结果表明，温度场对比例电磁铁的影响可以分为两个方面：①温度对线圈的影响，使线圈内阻增大，甚至导致线圈短路失效，是影响电磁阀寿命的主要原因；②温度场对结构参数的影响，由温度而产生的热应力会引起隔磁环结构参数发生变化，影响磁场性能，对电磁力、电感有直接影响，结构参数变化还会改变阀芯受到的摩擦力、阻尼力，影响电磁阀的动态性能和稳定性；③环境温度也能够影响电磁阀工作性能，甚至影响电磁阀的使用寿命.

图11 显示有无温度影响的电磁力对比图，随着温度的升高，电磁力的线性度越差. 图12 显示了电磁阀在不同工作条件下，环境温度与线圈温升的关系. 在不同的环境温度下，温度场对电磁阀的影响也不同. 例如车辆在启动阶段与稳定工作阶段，自动变速箱内的油温不同，从而导致相同控制条件下的电磁阀性能不同.

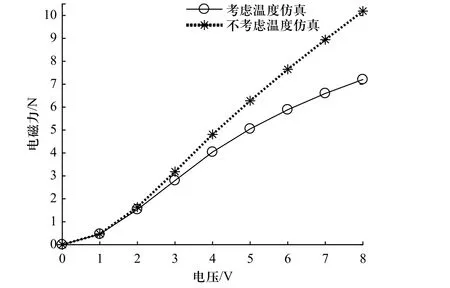
图11 有无温度影响的电磁力对比图Fig. 11 Comparison of electromagnetic force

图12 不同工作条件下，环境温度与线圈温升的关系Fig. 12 Relationship between ambient and coil temperature

4 试验验证

4.1 试验条件

为了能够验证该建模方法的准确性与可行性，本文分别设计了比例电磁铁与比例电磁阀的测试系统，其原理如图13（a）,13（b）所示，分别从稳态与瞬态两个方面进行仿真数据与试验数据的对比. 测试系统主要由液压泵站、直流电源、热电偶、电流传感器、油压传感器、电磁阀控制器、驱动电路及计算机，高精度力传感器等组成，关键设备参数如表1 所示.

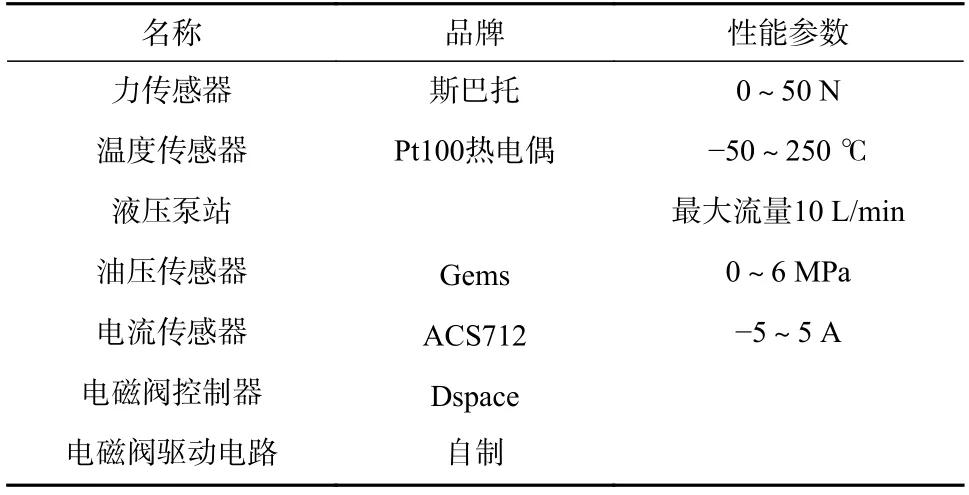
表1 比例电磁阀的关键参数Tab. 1 Key parameters of proportional solenoid valve

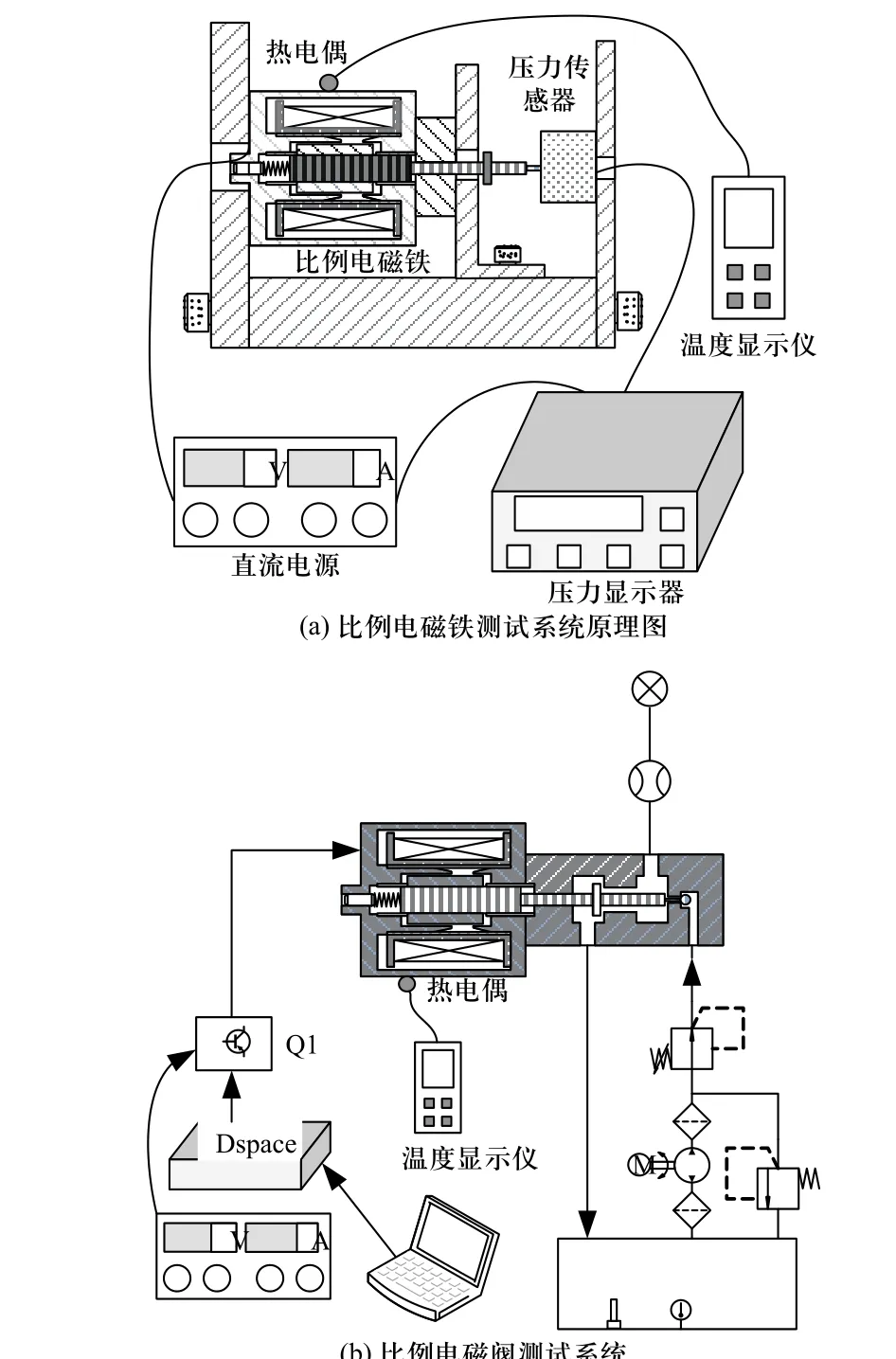
图13 测试系统原理图Fig. 13 Schematic diagram of the test system

在测试过程中，由于电磁铁内部温度无法测量，只能通过对比电磁阀外壳某一点处的温度变化. 输入电压范围选择为1～8 V，间隔为1 V，并控制环境温度为20 ℃. 在试验过程中，为保证温升达到稳定，当电磁阀分别在不同电压下工作时，每隔10 min 记录一次温度数据，直至温度不再上升，即温度达到稳态，然后分别测试电磁力和输出油压.

4.2 试验分析

4.2.1 电磁铁有限元模型验证

通过测试铁电磁铁的稳态特性数据，对2.1 节提出的有限元模型进行验证. 主要采集的测试数据是温度稳定时，温度与电压、电流与电压、电阻与电压及电磁力与电压之间关系；瞬态特性测试的是当温度稳定时，电流与输出油压随时间的变化特性.

图14（a）～14（c）显示了比例电磁铁的外壳某一点处的稳定温度、稳态电流、电磁力的仿真与试验数据对比结果. 在图14（a）的温度随电压的变化关系，两者的最大相对误差为1%，仿真与试验的温度变化趋势基本一致；在图14（b）的稳态电流对比图中，随着温度的升高，电流的增长呈非线性变化，最大相对误差小于1%；在图14（c）的电磁力对比图中，最大相对误差为2.2%，增长趋势基本一致. 通过对稳态数据进行比较，验证了比例电磁铁电磁场与温度场耦合模型的准确性，并且可以基于该模型进一步详细分析环境温度、线圈发热的共同作用对电磁铁特性的影响.

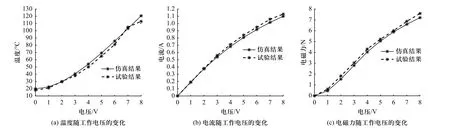
图14 稳态温度时的仿真与试验数据对比Fig. 14 Comparison of simulation and experimental data at steady state temperature

4.2.2 比例电磁阀油压输出特性验证

基于第3 部分得到的电磁铁在不同条件下的数据集，利用Matlab/Simulink 软件比例电磁阀的系统仿真模型，对电磁阀的动态输出特性进行仿真. 为了验证模型的准确性，利用搭建的电磁阀测试系统对模型进行验证. 设置测试环境温度为20 ℃、供油压力为0.65 MPa、输入电压为8 V 时的电磁阀动态特性. 测试数据分为两种：一是电磁阀在不考虑温度影响时的动态响应数据，如图15（a），15（b）所示；二是电磁阀工作一段时间后的动态响应数据，即考虑温度影响，如图16（a），16（b）所示.

图15 不考虑温度影响的动态响应对比Fig. 15 Dynamic comparison without temperature

当不考虑温度影响时，电流达到稳定时大约需要15 ms，稳定电流大约是1.55 A，仿真数据与试验数据基本吻合，图15（a）所示，其误差原因可能是电磁阀在测试过程中，不能保证电磁阀处于绝对的环境温度，线圈会有少量的温升；在图15（b）所示油压动态响应数据对比中，油压在3 ms 时开始上升，油压达到0.65 MPa 时的时间大约是5.5 ms，仿真数据与试验数据的上升趋势基本一致. 当考虑温度的影响时，电流达到稳定时大约需要18 ms，稳定电流大约是1.1 A，仿真数据与试验数据基本吻合，图16（a）所示；在图16（b）所示油压动态响应数据对比中，油压在5 ms 时开始上升，油压达到0.65 MPa 时的时间大约为10 ms，除测试油压在上升过程中存在较大波动外，仿真数据与试验数据的上升趋势基本一致. 通过对比分析得到，温度场对电磁阀动态特性有明显的影响，较高的温度会减小电磁阀阀芯与阀孔的配合间隙，增加了阀芯所受的摩擦力、阻尼力，从而降低了油压的响应速度.

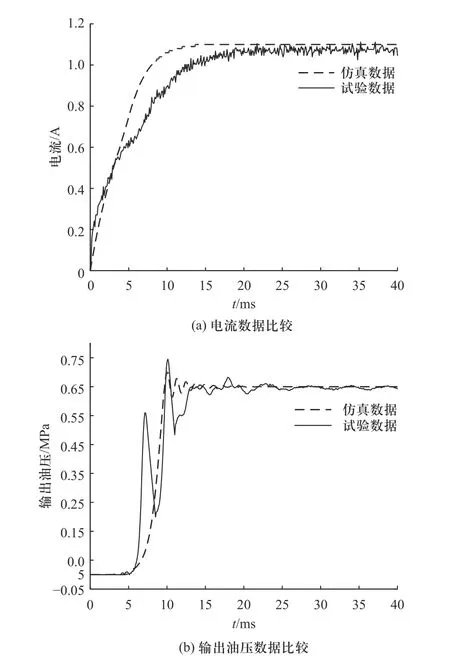
图16 考虑温度影响的动态响应对比Fig. 16 Dynamic comparison with temperature

通过上述的数据对比，验证了本文所提出的考虑温度的系统动态建模方法的可行性和正确性.

5 结 论

提出了一种用于分析热效应对电磁阀动态性能影响的建模方法. 首先，利用FEM 建立比例电磁铁模型，并通过搭建的电磁铁试验台验证模型的准确性；其次，利用该模型分析在不同的环境温度和工作条件下温度场分布、热应力分布、结构变形对比例电磁铁输出力特性的影响；然后，将包含温度场的比例电磁铁数据集、系统动力学和流体力学方程相结合，建立比例电磁阀的系统动态模型；最后，通过搭建比例电磁阀测试平台验证了系统模型的准确性.

研究结果表明：①电磁阀在工作过程中，温度分布最高的区域集中在线圈内部，随温度升高，隔磁环结构处的变形量也增大；②在相同工作电压下，环境温度升高会促进电磁铁的温升，也是影响电磁阀工作寿命的重要因素之一；③温度场使得电磁阀发生结构变形，从而影响系统动力学参数，降低电磁阀的动态响应速度，当电压为8 V 时，电磁阀启动时间延迟了2 ms，建压时间延迟了3 ms；④通过仿真与试验数据结果比较，两者在数值变化趋势上较为吻合，数值偏差在合理范围内，验证了本文提出的建模方法能够准确地分析、评估温度场对电磁阀动态性能的影响，为电磁阀的设计和优化提供有力的依据.